�T�C�N���@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�M�@�ւ����낢��ȉߒ����o�Č��̏�Ԃɖ߂��Ă��邱�Ƃ��J��Ԃ��Ƃ��A����Ԃ���1���T�C�N���ƌ����B
1�T�C�N���ŋC�̂��O���ɂ��鐳�����d���́Ap�|V�O���t�̈͂ޖʐςɓ������B
����@1�T�C�N���ŋC�̂��O���ɂ��鐳�����d���́A�C�̂��O���������d������A�O��������ꂽ�d�������������̂ł��B
 �E�}(a)�ŁAA��B��p�|V�O���t��V���̊Ԃɋ��܂ꂽ����(���ΐF�̕����Ɛ��F�̕���)�̖ʐς��A�C�̂��O���ɂ��������d��
�E�}(a)�ŁAA��B��p�|V�O���t��V���̊Ԃɋ��܂ꂽ����(���ΐF�̕����Ɛ��F�̕���)�̖ʐς��A�C�̂��O���ɂ��������d�� ��\���܂�(�C�̂̂����d�����Q��)�BB��A��p�|V�O���t��V���̊Ԃɋ��܂ꂽ����(���F�̕���)�̖ʐς��A�C�̂��O�����炳�ꂽ�����d��
��\���܂�(�C�̂̂����d�����Q��)�BB��A��p�|V�O���t��V���̊Ԃɋ��܂ꂽ����(���F�̕���)�̖ʐς��A�C�̂��O�����炳�ꂽ�����d�� ��\���܂��B
��\���܂��B
�C�̂������������d�� �́AA��B��A��p�|V�O���t�ň͂܂ꂽ����(���ΐF�̕���)�̖ʐςɂȂ�܂��B�E�}(a)(p�|V�O���t���E����ł�)�ł́A
�́AA��B��A��p�|V�O���t�ň͂܂ꂽ����(���ΐF�̕���)�̖ʐςɂȂ�܂��B�E�}(a)(p�|V�O���t���E����ł�)�ł́A �C�܂�A�C�̂͊O���ɑ��Đ����d�������܂��B
�C�܂�A�C�̂͊O���ɑ��Đ����d�������܂��B
�E�}(b)( p�|V�O���t��������ł�)�ł́A �C�܂�A�C�̂͊O�����琳���d������������ƂɂȂ�܂��B
�C�܂�A�C�̂͊O�����琳���d������������ƂɂȂ�܂��B
�܂��A1�T�C�N���Ō������x�ɖ߂��Ă���̂ŁA���x�ω���0�ł���A�C�̂������G�l���M�[�̕ω� ��0�ł��B
��0�ł��B
�]���āA1�T�C�N���ŋC�̂��z�������M��Q�Ƃ���ƁA�M�͊w���@�����A �ƂȂ�܂��B
�ƂȂ�܂��B
 ��1�@�E�}�̃T�C�N���ł́A(����p�C�̐�V�C��Ή��xT)���A���1�F
��1�@�E�}�̃T�C�N���ł́A(����p�C�̐�V�C��Ή��xT)���A���1�F �����2�F
�����2�F �����3�F
�����3�F �����4�F
�����4�F �����1�F
�����1�F �̏��ɕω����܂��B
�̏��ɕω����܂��B�e��Ԃɂ����āA��ԕ������A �C
�C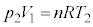 �C
�C �C
�C ���������܂��B
���������܂��B
�C�̂̒�σ�����M�� �C�舳������M��
�C�舳������M�� �Ƃ���(������M���Q��)�A
�Ƃ���(������M���Q��)�A
���1�����2����ϕω��ŋC�̂̂����d����0�C�C�̂��z�������M�́A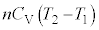
���2�����3���舳�ω��ŋC�̂̂����d���� �C�C�̂��z�������M�́A
�C�C�̂��z�������M�́A
���3�����4�͒�ϕω��ŋC�̂̂����d����0�C�C�̂��z�������M�́A
���4�����1�͒舳�ω��ŋC�̂̂����d���� �C�C�̂��z�������M�́A
�C�C�̂��z�������M�́A 1�T�C�N���ŋC�̂��O���ɂ����������d���́A
1�T�C�N���ŋC�̂��O���ɂ����������d���́A �C�C�̂��z�������M�́A
�C�C�̂��z�������M�́A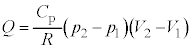 �C�M����η�́A
�C�M����η�́A
 ��2�@�E�}�̃T�C�N���ł́A(����p�C�̐�V�C��Ή��xT)���A���1�F
��2�@�E�}�̃T�C�N���ł́A(����p�C�̐�V�C��Ή��xT)���A���1�F �����2�F
�����2�F �����3�F
�����3�F �����1�F
�����1�F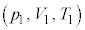 �̏��ɕω����܂��B
�̏��ɕω����܂��B�e��Ԃɂ����āA��ԕ������A �C
�C �C
�C ���������܂��B
���������܂��B
���1�����2����ϕω��A���3�����1���舳�ω��ł��B
���2�����3�������ω��ŁA�C�̂��z�������MQ�ƋC�̂̂����d��W�͂Ƃ��ɁA 1�T�C�N���ŋC�̂��O���ɂ����������d���́A
�C�̂��z�������M��Q�C�M����η�́A
 ��3 �E�}(a)�̃T�C�N���ł́A(����p�C�̐�V�C��Ή��xT)���A���1�F
��3 �E�}(a)�̃T�C�N���ł́A(����p�C�̐�V�C��Ή��xT)���A���1�F �����2�F
�����2�F �����3�F
�����3�F �����4�F
�����4�F �����1�F
�����1�F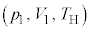 �̏��ɕω����܂��B
�̏��ɕω����܂��B���1�����2�ɂ����ċC�͍̂��M���ɐڐG���������ω��Ŗc�����A���2�����3�ł͔M���Ƃ̐ڐG��f�����f�M�c�����A���3�����4�ɂ����Ē�M���ɐڐG���������ω��ň��k����A���4�����1�ł͔M���Ƃ̐ڐG��f�����f�M���k����܂��B���̃T�C�N�����J���m�[�E�T�C�N���ƌ����܂��B
�e��Ԃɂ����āA��ԕ������A �C
�C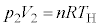 �C
�C �C
�C ���������܂��B
���������܂��B
���2�����3�Ə��4�����1���f�M�ω��ł́A�C�̂���M����γ�Ƃ��āA�|�A�b�\���̊W���F �C
�C ���������܂��B
���������܂��B
��ԕ��������A �C
�C
�|�A�b�\���̊W�����A
�]���āA �C����āA
�C����āA �@����@
�@����@
���1�����2�������ω��ł́A�C�̂������d�� �ƋC�̂��z�������M
�ƋC�̂��z�������M ���������A
���������A

���3�����4�������ω��ł́A�C�̂����ꂽ�d�� �ƋC�̂����o�����M
�ƋC�̂����o�����M ���������A
���������A

�C�̂�1�T�C�N���ł����d�� �́A�E��}(a)�̉��ΐF�����̖ʐςɂȂ�܂��B
�́A�E��}(a)�̉��ΐF�����̖ʐςɂȂ�܂��B
�@��p���āA
������A�J���m�[�E�T�C�N���ɂ�����M����η�́A

�J���m�[�E�T�C�N���ł́A�M�����͍��M���ƒ�M�������x�Ō��܂�܂��B�������I�ȔM�@�ւ���邽�߂ɂ́A���M���̉��x�������A��M���̉��x��Ⴍ�Ƃ�悢���Ƃ��킩��܂��B
�E��}(a)��p�|V�O���t�ł́A�E����Ȃ̂ŁA�C�̂͊O���ɑ��Đ����d��������̂ł����A���̂Ƃ��A �Ȃ̂ŁA�C�̂͊O�������M���z�����ĊO���ɑ����d�������邱�ƂɂȂ�܂��B
�Ȃ̂ŁA�C�̂͊O�������M���z�����ĊO���ɑ����d�������邱�ƂɂȂ�܂��B
�E��}(b)��p�|V�O���t�ł́A������ł��B���̂Ƃ��́A ���C�̂��z�������M�A
���C�̂��z�������M�A ���C�̂����o�����M�ƂȂ�A�C�̂́A�O�����琳���d��(�E��}(b)�̉��ΐF�����̖ʐ�)������邱�Ƃɂ���āA��M�������M��D���A���M�����M���̂Ă�悤�ȓ�������܂��B���ꂪ��[�@��A�①�ɂ̌����ł��B
���C�̂����o�����M�ƂȂ�A�C�̂́A�O�����琳���d��(�E��}(b)�̉��ΐF�����̖ʐ�)������邱�Ƃɂ���āA��M�������M��D���A���M�����M���̂Ă�悤�ȓ�������܂��B���ꂪ��[�@��A�①�ɂ̌����ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 


 �C
�C

 �C����āA
�C����āA �@����@
�@����@


