エントロピー
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
基準となる熱平衡状態Cから熱平衡状態Aまで連続的準静的に変化(可逆変化)するとき(不可逆変化を参照)、変化の過程で温度Tの熱源から熱 を吸収するとして、
を吸収するとして、
 ・・・①
・・・① を状態Aにおけるエントロピーと言います。エントロピーは内部エネルギーのように各状態ごとに定まる量です。熱平衡状態Aから熱平衡状態Bまで連続的準静的に変化(可逆変化)するときのエントロピーの変化
を状態Aにおけるエントロピーと言います。エントロピーは内部エネルギーのように各状態ごとに定まる量です。熱平衡状態Aから熱平衡状態Bまで連続的準静的に変化(可逆変化)するときのエントロピーの変化 は、AからBまでの変化の過程によらず、
は、AからBまでの変化の過程によらず、
 (
( )
)
となります。温度Tにおけるエントロピーの微小変化分 については、
については、
 ・・・②
・・・②
nモルの理想気体が熱Qを吸収し内部エネルギーを だけ変化させて外部に仕事Wをするとき、熱力学第一法則より、
だけ変化させて外部に仕事Wをするとき、熱力学第一法則より、 となりますが、変化の過程における気体の圧力をp,体積をVとして、微小変化分
となりますが、変化の過程における気体の圧力をp,体積をVとして、微小変化分 について、
について、 (
( ,気体のした仕事を参照),
,気体のした仕事を参照), (
( ,内部エネルギーを参照)より、
,内部エネルギーを参照)より、
 ・・・③
・・・③
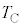 ,体積
,体積 )から熱平衡状態A (温度
)から熱平衡状態A (温度 ,体積
,体積 )まで積分すると、Aにおける理想気体のエントロピー
)まで積分すると、Aにおける理想気体のエントロピー は、気体定数をRとして、状態方程式
は、気体定数をRとして、状態方程式 より、
より、
 とおいて、温度T,体積Vの状態でのnモルの理想気体のエントロピーSは、
とおいて、温度T,体積Vの状態でのnモルの理想気体のエントロピーSは、
 (
( :定数) ・・・④
:定数) ・・・④
比熱比 (断熱変化を参照)を用いると、
(断熱変化を参照)を用いると、 となるので、④は、
となるので、④は、
となります。準静的な断熱変化A→Bでは、変化の過程で気体は熱を吸収しないので、エントロピーの変化は、 です。S一定となるので、
です。S一定となるので、 ,つまり、
,つまり、 となり、ポアッソンの関係式が得られます。
となり、ポアッソンの関係式が得られます。
nモルの気体が、体積 ,温度T,エントロピー
,温度T,エントロピー の状態から体積
の状態から体積 ,温度T,
,温度T, の状態まで変化するときのエントロピーの変化
の状態まで変化するときのエントロピーの変化 は、④より、
は、④より、
 のときには
のときには ,
, のときには
のときには です。この変化が等温変化の場合には変化の過程は準静的で可逆変化なので、A→B→Aと変化すると、
です。この変化が等温変化の場合には変化の過程は準静的で可逆変化なので、A→B→Aと変化すると、 より、エントロピーの変化はゼロです。ですが、この変化が自由膨張(真空への膨張、気体のした仕事を参照)の場合(
より、エントロピーの変化はゼロです。ですが、この変化が自由膨張(真空への膨張、気体のした仕事を参照)の場合( )には不可逆変化で、A→Bにおいて
)には不可逆変化で、A→Bにおいて となります。
となります。
その他、ピストンとシリンダーの間に摩擦があって熱を発生する場合なども含めて、不可逆変化では、エントロピーは増大します。これをエントロピー増大の法則と言います。準静的過程は理想的な過程であって、現実的にはすべての過程が不可逆変化で、この宇宙は、エントロピーが増大する方向に一方的に変化し続けていると言うことができます。
④は、単原子分子理想気体の場合、 と、
と、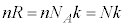 (
( :アボガドロ数、N:気体の分子数、k:ボルツマン定数)より、
:アボガドロ数、N:気体の分子数、k:ボルツマン定数)より、
 ・・・⑤
・・・⑤
 (ここに、
(ここに、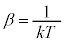 )
) は、
は、 となるので、
となるので、
この式の は定数なので、⑤のSをkで割ったものとの差は定数です。これより、単原子分子理想気体の場合、エントロピーは分配関数Zを用いて、
は定数なので、⑤のSをkで割ったものとの差は定数です。これより、単原子分子理想気体の場合、エントロピーは分配関数Zを用いて、
と表すことができます。この結果は、統計力学の様々なモデルで成立し、ボルツマンの原理と呼ばれています。
区別できないN個の粒子からなるcanonical ensemble(正準集団)においては、J個のセルのうちのエネルギー の j番目(
の j番目( )のセルに
)のセルに 個のセルが入る確率
個のセルが入る確率 は、
は、 として、
として、
ここで、全確率: となっています。
となっています。
全エネルギー、つまり内部エネルギーをUとして、粒子1個のエネルギーの期待値 は、
は、
ここで、分配関数Zはこの分母で、
 をβ で微分すると、
をβ で微分すると、
よって、 より、内部エネルギーは、
より、内部エネルギーは、
で与えられます。 より
より ,
, より、
より、
 ・・・⑥
・・・⑥
⑥より、 ,よって、
,よって、
また、 より、
より、 ,これを用いて、
,これを用いて、
ここで、 (導出は省略します)を用いて、
(導出は省略します)を用いて、
 ∴
∴ 
 ∴
∴ 
 ,
, ,
, を用いて、エントロピーは、
を用いて、エントロピーは、
 より、エントロピーを
より、エントロピーを
と書くことができます。
コンピューターの内部では'0'と'1'の2つの数を用いて情報を表します。
1個の変数 が0か1という数値を同様に確からしく取り得るとします。
が0か1という数値を同様に確からしく取り得るとします。 となる確率
となる確率 ,
, となる確率
となる確率 は、それぞれ、
は、それぞれ、
です。このとき、 という量を考えます。
という量を考えます。
2個の変数 ,
, がそれぞれ数値0,1を同様に確からしく取り得るとします。
がそれぞれ数値0,1を同様に確からしく取り得るとします。 ,
, の取り得る状態を2つ数字を並べて書くと、00,01,10,11の4通りあります。それぞれの確率を
の取り得る状態を2つ数字を並べて書くと、00,01,10,11の4通りあります。それぞれの確率を ,
, ,
, ,
, とすると、
とすると、
です。このとき、 は、
は、
変数3個 ,
, ,
, の場合は、
の場合は、 ,
, ,
, の取り得る状態を3つの数字を並べて書くと、000,001,010,011,100,101,110,111の8通りあります。それぞれの確率を
の取り得る状態を3つの数字を並べて書くと、000,001,010,011,100,101,110,111の8通りあります。それぞれの確率を ~
~ とすると、
とすると、 で、
で、 は、
は、
同様に変数4個の場合は、0000,0001,~,1111の16通りの確率は、それぞれ、
変数8個の場合は、00000000,00000001,~,11111111の256通りの確率は、それぞれ、
変数n個の場合は、 通りのそれぞれの確率は、
通りのそれぞれの確率は、
Hは情報量を表しており、情報理論でエントロピーと言います。熱力学、統計力学のエントロピーと対応しています。上記の例では変数の数に一致していることがわかります。この変数の数をビットと言います。8ビットで1バイトと言います。1Kバイトは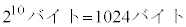 ,
, ,
, ,
, より、
より、  のハード・ディスク・ドライブは、
のハード・ディスク・ドライブは、 通り(
通り( より、10進法で280兆ビット、2バイト1文字として
より、10進法で280兆ビット、2バイト1文字として ,つまり43億文字、本1000冊分)の情報を扱えます。
,つまり43億文字、本1000冊分)の情報を扱えます。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理基礎事項TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。  (断熱変化を参照)を用いると、
(断熱変化を参照)を用いると、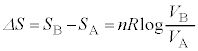
 より、エントロピーの変化はゼロです。ですが、この変化が自由膨張(真空への膨張、気体のした仕事を参照)の場合(
より、エントロピーの変化はゼロです。ですが、この変化が自由膨張(真空への膨張、気体のした仕事を参照)の場合( (ここに、
(ここに、

 は定数なので、⑤のSをkで割ったものとの差は定数です。これより、単原子分子理想気体の場合、エントロピーは分配関数Zを用いて、
は定数なので、⑤のSをkで割ったものとの差は定数です。これより、単原子分子理想気体の場合、エントロピーは分配関数Zを用いて、
 となっています。
となっています。


 (導出は省略します)を用いて、
(導出は省略します)を用いて、 ,
, ,
,

 より、エントロピーを
より、エントロピーを
 という量を考えます。
という量を考えます。 は、
は、 は、
は、

