������Ȏ��ȑ啨��'09�N[1]
�n�\�ɑ��ď㉺(��������)�Ɏ��R�ɓ������Ƃ��ł��������������A���̒��Ŏ���������B�������̉^���͒n�\�ɒu���ꂽ���W�n�ōl���A������(�傫���͖����ł���)�̎����ɂ��Ă͎������ɌŒ肳�ꂽ���W�n�ōl������̂Ƃ���B�d�͉����x�̑傫����g�Ƃ���B�܂��A�������̉����xa�͉���������𐳂Ƃ��ĕ\���A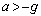 �͈̔͂ɂ�����̂Ƃ���B
�͈̔͂ɂ�����̂Ƃ���B
�ȉ��̊e�₢�ɓ�����B
 �������̓V��ɁA�o�l�萔��k�Ŏ��R����
�������̓V��ɁA�o�l�萔��k�Ŏ��R����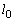 �ł���y���o�l���Œ肵�Ă���B���������Î~���Ă�����
�ł���y���o�l���Œ肵�Ă���B���������Î~���Ă�����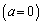 �ŁA�o�l�̑��[�Ɏ���m�̂�����������Ƃ���A�o�l��
�ŁA�o�l�̑��[�Ɏ���m�̂�����������Ƃ���A�o�l��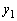 �����L�тĐÎ~����(�}1)�B
�����L�тĐÎ~����(�}1)�B
��1�@�o�l�̐L�� �����߂�B
�����߂�B
�荇���̈ʒu����o�l��d�����̂��A�����Ǝ�𗣂��ƃo�l�͏㉺�����ɒP�U�����n�߂��B
��2�@���̂Ƃ��̃o�l�̐U���̎���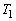 �����߂�B
�����߂�B ��3�@������̍ő�̑���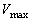 �Ƃ��̂Ƃ��̃o�l�̒���L�����߂�B
�Ƃ��̂Ƃ��̃o�l�̒���L�����߂�B ��4�@�U���̓r���A�o�l�̒������ŏ��ɂȂ����Ƃ��ɁA�����������̉����xa�œ����n�߂��B��������������������̃o�l�̐U���̐U��A�Ǝ��� �����߂�B�������A���̉����xa�ɒB����܂ł̎��ԂƂ��̊Ԃ̂�����̕ψʂ͖����ł�����̂Ƃ���B
�����߂�B�������A���̉����xa�ɒB����܂ł̎��ԂƂ��̊Ԃ̂�����̕ψʂ͖����ł�����̂Ƃ���B
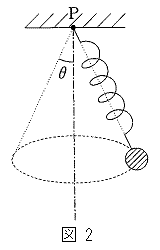 ���ɁA�����������̉����xa�œ����Ă������ŁA�}2�̂悤�ɌŒ�_P��ʂ鉔�����ƃo�l�̂Ȃ��p��θ �ƂȂ�悤�ɂ����肪�����ʓ��ʼn�]������ƁA�o�l�̐L�т�
���ɁA�����������̉����xa�œ����Ă������ŁA�}2�̂悤�ɌŒ�_P��ʂ鉔�����ƃo�l�̂Ȃ��p��θ �ƂȂ�悤�ɂ����肪�����ʓ��ʼn�]������ƁA�o�l�̐L�т�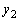 �ƂȂ����B��]���Ƀo�l�͓r���ŋȂ������肹���A�L�т͕ς��Ȃ����̂Ƃ���B
�ƂȂ����B��]���Ƀo�l�͓r���ŋȂ������肹���A�L�т͕ς��Ȃ����̂Ƃ���B
��5�@���̂Ƃ��A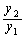 �C����щ�]�^���̎���
�C����щ�]�^���̎���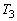 �����߂�B
�����߂�B
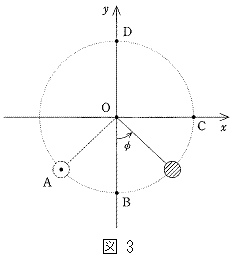 �����������������̉����xa�œ����Ă������ŁA�ʂ̎������s�����B����r�̐L�яk�݂��Ȃ��y�����̈�[�Ɏ���m�̂������t���A���[���������̑��ǂɌŒ肵���B������͑��ǂɂ����ĉ������ʓ������R�ɉ�]�ł��邪�A������Ƒ��ǂ̊Ԃɖ��C�͓����Ȃ����̂Ƃ���B�}3�̂悤�ɌŒ�_�����_O�ɁA����������x���A����������y�����Ƃ�A������͔����v���ɓ_A�C�_B�C�_C�C�_D�̏��Ɋe�_��ʂ���̂Ƃ���B�������A��]�pϕ�͐}3�̂悤�ɓ_B���甽���v�܂��ɂƂ�A
�����������������̉����xa�œ����Ă������ŁA�ʂ̎������s�����B����r�̐L�яk�݂��Ȃ��y�����̈�[�Ɏ���m�̂������t���A���[���������̑��ǂɌŒ肵���B������͑��ǂɂ����ĉ������ʓ������R�ɉ�]�ł��邪�A������Ƒ��ǂ̊Ԃɖ��C�͓����Ȃ����̂Ƃ���B�}3�̂悤�ɌŒ�_�����_O�ɁA����������x���A����������y�����Ƃ�A������͔����v���ɓ_A�C�_B�C�_C�C�_D�̏��Ɋe�_��ʂ���̂Ƃ���B�������A��]�pϕ�͐}3�̂悤�ɓ_B���甽���v�܂��ɂƂ�A (
( )�Ƃ���B
)�Ƃ���B
��6�@�_A�̈ʒu�ł������Â��ɕ������B�ʼn��_B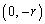 �ł̎��̒��͂̑傫��S�����߂�B
�ł̎��̒��͂̑傫��S�����߂�B ��7�@�����肪�_A���瓮�������AA��B��C��D���Ə��ɒʂ��Ĉ��]���邽�߂ɂ́A�_A�ʼn~(�_��)�̐ڐ�����(�E������)�ɂǂ̂��炢�̑����ł����������Ȃ���Ȃ�Ȃ����B���̍ŏ��̑���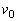 �����߂�B
�����߂�B ��8�@��7�ŋ��߂�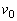 �œ_A���炨�������Ƃ��A�����ꂸ�ɂ����肪��]�^�������邽�߂̎������̉����xa�͈̔͂����߂�B�������A���̎��͋��x�Ɍ��E������Î~�������������ŁA���ʂ�
�œ_A���炨�������Ƃ��A�����ꂸ�ɂ����肪��]�^�������邽�߂̎������̉����xa�͈̔͂����߂�B�������A���̎��͋��x�Ɍ��E������Î~�������������ŁA���ʂ�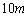 �ȏ�̂���������ĉ����ɐ��炵���Ƃ��ɐ����̂Ƃ���B
�ȏ�̂���������ĉ����ɐ��炵���Ƃ��ɐ����̂Ƃ���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��4�܂ł͒P�U���̊�b���A��5�̓o�l�t���~���U��q�̖��ł��B��6�ȍ~���s�����~�^���ŁA�d���ɂ���ʒu�G�l���M�[���l����Ƃ��́A������������̂ŁA�d�͉����xg�ł͂Ȃ��A�������̏d�͉����x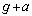 ���g���čl���邱�Ƃɒ��ӂ��Ă��������B��9��
���g���čl���邱�Ƃɒ��ӂ��Ă��������B��9�� �Ƃ��������͌��ʂɉe�����܂���B�ǂ��ł����������Ă��A�ŏ�_(D�_)�Ŏ���������0�ɂȂ�悤�������x��^����A��������^���G�l���M�[��ϕ�ˑ����͓����ł��B
�Ƃ��������͌��ʂɉe�����܂���B�ǂ��ł����������Ă��A�ŏ�_(D�_)�Ŏ���������0�ɂȂ�悤�������x��^����A��������^���G�l���M�[��ϕ�ˑ����͓����ł��B
�� 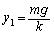 ......[��]
......[��] ����́A�p�U����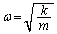 ���P�U����\���܂��B�����́A
���P�U����\���܂��B�����́A  ......[��]
......[��]��3�@�ŏ��ɂ荇���̈ʒu(�U�����S)����d�����o�l��L���������x0�ŕ������̂ŁA�������ʒu���U���[�ƂȂ�A�U����d�ł��B
��4�@�o�l���������ŏ��̂Ƃ��A�o�l�͐U�����S(�荇���̈ʒu)���d�����k��ł���̂ŁA���̂Ƃ��̃o�l���L����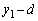 �ł��B
�ł��B �������������xa�œ��������A�d�͉����xg�����������d�͉����x �ɕς���Ă��A�o�l�萔k�Ƃ����������m�ɂ͕ω��͂Ȃ��A�P�U�����������ω����܂���B
�ɕς���Ă��A�o�l�萔k�Ƃ����������m�ɂ͕ω��͂Ȃ��A�P�U�����������ω����܂���B 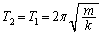 ......[��]
......[��]�������������xa�œ��������ƁA������ɂ�������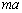 �������܂��B���̂Ƃ��̃o�l���L����
�������܂��B���̂Ƃ��̃o�l���L����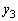 �Ƃ��āA������ɓ����͂̂荇�����A
�Ƃ��āA������ɓ����͂̂荇�����A �� 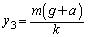 ���̂Ƃ��̒P�U�����U��A�́A�U���[�ɂ�����o�l���L��
���̂Ƃ��̒P�U�����U��A�́A�U���[�ɂ�����o�l���L��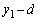 �ƐU�����S�ɂ�����o�l���L��
�ƐU�����S�ɂ�����o�l���L��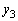 �Ƃ̍��̐�Βl�ɓ������A
�Ƃ̍��̐�Βl�ɓ������A 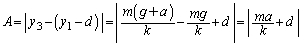 ......[��]
......[��]��5�@���������ł̂�����ɓ����͂̂荇�����A
��  ��
�� 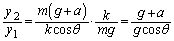 ......[��]������͐����ʓ������a
......[��]������͐����ʓ������a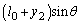 �ʼn~����`���������~�^�����܂��B���S���́A������ɓ����o�l���e����
�ʼn~����`���������~�^�����܂��B���S���́A������ɓ����o�l���e����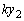 �̐�����������
�̐����������� �ŁA�����~�^�����p���x��ω�Ƃ��āA������̌��S�������^���������́A
�ŁA�����~�^�����p���x��ω�Ƃ��āA������̌��S�������^���������́A �� 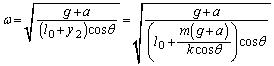
��]�^���������́A
 ......[��]
......[��]��6�@�ʼn��_(B�_)�ɂ������^���������́A����������S�C�������������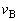 �Ƃ��āA
�Ƃ��āA 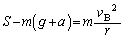 �@����@
�@����@�ʼn��_���d�����ʒu�G�l���M�[�̊�Ƃ��āAA�_�ɂ������͊w�I�G�l���M�[�́A�ʒu�G�l���M�[ �݂̂ŁA�ʼn��_�ɂ������͊w�I�G�l���M�[�́A�^���G�l���M�[
�݂̂ŁA�ʼn��_�ɂ������͊w�I�G�l���M�[�́A�^���G�l���M�[ �݂̂ł��B�͊w�I�G�l���M�[�ۑ����A
�݂̂ł��B�͊w�I�G�l���M�[�ۑ����A 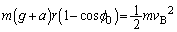 �@����A
�@����A�@�C�A��� ���������āA
���������āA �� 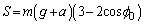 ......[��]
......[��] ��7�@�����肪���]���邽�߂ɂ́A�ŏ�_(D�_)�ŁA�������� �ł���K�v������܂��B
�ł���K�v������܂��B �������������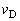 �Ƃ��āA�ŏ�_�ɂ������^���������́A
�Ƃ��āA�ŏ�_�ɂ������^���������́A 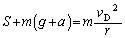 �@����B
�@����B�ŏ�_�ɂ������͊w�I�G�l���M�[�́A�^���G�l���M�[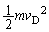 ���ʒu�G�l���M�[
���ʒu�G�l���M�[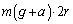 �ł��B�����ł́AA�_�ŕ����Ƃ��������x
�ł��B�����ł́AA�_�ŕ����Ƃ��������x ��^����̂��^���G�l���M�[
��^����̂��^���G�l���M�[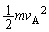 ������܂��BA�_�ƍŏ�_�Ƃ��͊w�I�G�l���M�[�ۑ����A
������܂��BA�_�ƍŏ�_�Ƃ��͊w�I�G�l���M�[�ۑ����A �� 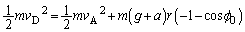 �@����C
�@����C
�B�C�C���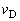 ���������āA
���������āA �� 
 ���A
���A ��  ......[��]
......[��] ��8�@��7���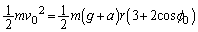
����āAA�_�ɂ������͊w�I�G�l���M�[�́A
A�_�Ɖ�]�pϕ�̎��_(�������������v�Ƃ��܂�)�Ƃɂ������͊w�I�G�l���M�[�ۑ����A

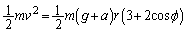 �@����D
�@����D��]�pϕ�̎��_�ł��^���������F
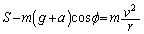 �@����E
�@����E�D�C�E���v����������ƁA
�� 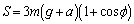
 �ɂ����ẮA
�ɂ����ẮA �̂Ƃ���S�͍ő�l
�̂Ƃ���S�͍ő�l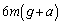 ���Ƃ�܂��B������Ȃ������́A
���Ƃ�܂��B������Ȃ������́A 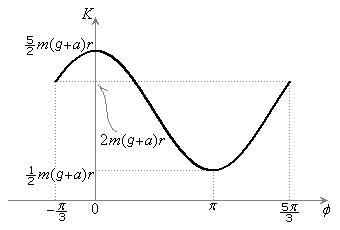 ��9�@�D���A��������^���G�l���M�[K�́A
��9�@�D���A��������^���G�l���M�[K�́A
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B