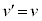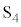��啨��'24�N�O��[2]
����(���E)�����̖_�ɋy�ڂ��e�����l����B������(xy����)����x���ƕ��s��2�{�̓��̃��[�����Ԋud�Őݒu����Ă���B2�{�̃��[����ɂ́A����m�̓��̖_��y���ƕ��s�ɒu����Ă���A���̖_�̓��[�����x���ƕ��s�ȕ����ɖ��C�Ȃ��Ɋ��邱�Ƃ��ł���B�������A���[���͏\���ɒ����A���̖_���^�����Ă����[���ォ��O��邱�Ƃ͂Ȃ��B�ȉ��̖�ł́A���[���A���̖_�⓱���̒�R�Ƒ����͖������Ă悭�A�����ɗ����d���ɂ�萶���鎥��A����сA�R�C���ȊO�̉�H�̎��ȃC���_�N�^���X���������Ă悢�B
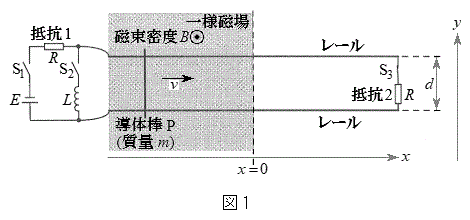 �T�D�����ł́A���[����̓��̖_��P�Ƃ�ԁB�}1�̂悤�ɁA
�T�D�����ł́A���[����̓��̖_��P�Ƃ�ԁB�}1�̂悤�ɁA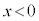 �̗̈�̃��[���̒[���ɁA������R���ł���N�d��E�̓d�r�A��R�lR�̒�R1�C���ȃC���_�N�^���XL�̃R�C���A����сA�X�C�b�`
�̗̈�̃��[���̒[���ɁA������R���ł���N�d��E�̓d�r�A��R�lR�̒�R1�C���ȃC���_�N�^���XL�̃R�C���A����сA�X�C�b�`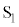 ��
��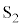 ���Őڑ������B����ɁA
���Őڑ������B����ɁA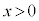 �̗̈�̃��[���̒[���ɂ́A��R�lR�̒�R2�ƃX�C�b�`
�̗̈�̃��[���̒[���ɂ́A��R�lR�̒�R2�ƃX�C�b�`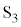 ���Őڑ������B
���Őڑ������B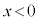 �̗̈�ɂ̂݁A���������(���ʂɐ����ɗ�����\����������)�̈�l�Ȏ��ꂪ����A���̎������x�̑傫����B�ł���B
�̗̈�ɂ̂݁A���������(���ʂɐ����ɗ�����\����������)�̈�l�Ȏ��ꂪ����A���̎������x�̑傫����B�ł���B�͂��߂ɁA�X�C�b�`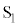 ��
��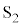 ���J�����܂܃X�C�b�`
���J�����܂܃X�C�b�`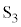 ����A���̖_P�ɊO�͂������A
����A���̖_P�ɊO�͂������A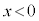 �̗̈�ɂ�����x���̐��̌����Ɉ��̑���v�œ��������B
�̗̈�ɂ�����x���̐��̌����Ɉ��̑���v�œ��������B
��1�@���̖_P�ɔ�������U���N�d�͂̑傫�������߂�B
��2�@���̖_P�ɉ����Ă���O�͂̑傫�������߂�B
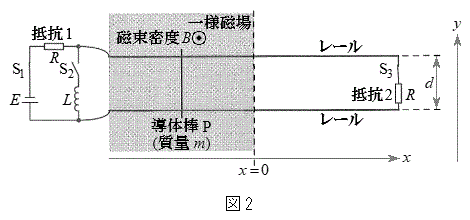 ���ɁA�}2�̂悤�ɁA�X�C�b�`
���ɁA�}2�̂悤�ɁA�X�C�b�`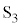 ������܂ܓ��̖_P��
������܂ܓ��̖_P��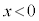 �̗̈��
�̗̈��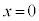 ����\���ɗ��ꂽ�ꏊ�ɐÎ~�����A����
����\���ɗ��ꂽ�ꏊ�ɐÎ~�����A����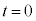 �ɃX�C�b�`
�ɃX�C�b�`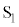 ������Ƃ���A���̖_P�������n�߂��B���̌サ�炭����ƁA���̖_P��
������Ƃ���A���̖_P�������n�߂��B���̌サ�炭����ƁA���̖_P��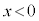 �̗̈���ň��̑��x�ɒB�����B
�̗̈���ň��̑��x�ɒB�����B
��3�@���̖_P�̑��x�����ɂȂ����Ƃ��̑��������߂�B  ��4�@�X�C�b�`
��4�@�X�C�b�`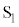 ����Ă��瓱�̖_P�̑��x�����ɂȂ�܂ł̊ԂɁA��R2�ɗ����d��
����Ă��瓱�̖_P�̑��x�����ɂȂ�܂ł̊ԂɁA��R2�ɗ����d��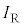 �̎��ԕω���}���������̂Ƃ��āA�ł��K�Ȃ��̂�}3��(��)����(��)�̒�����I��ŋL���œ�����B�������A��R2�𗬂��d���̐��̌�����y���̐��̌����Ƃ���B
�̎��ԕω���}���������̂Ƃ��āA�ł��K�Ȃ��̂�}3��(��)����(��)�̒�����I��ŋL���œ�����B�������A��R2�𗬂��d���̐��̌�����y���̐��̌����Ƃ���B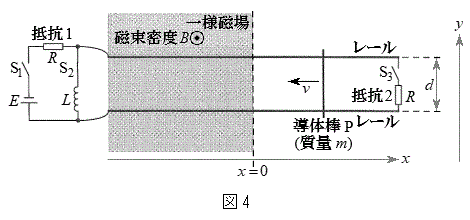 ���ɁA�X�C�b�`
���ɁA�X�C�b�`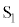 ��
��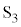 ���J���A���̖_P��
���J���A���̖_P��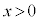 �̗̈�ŐÎ~�������B�����āA�}4�Ɏ����悤�ɁA�X�C�b�`
�̗̈�ŐÎ~�������B�����āA�}4�Ɏ����悤�ɁA�X�C�b�`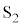 ����A���̖_P������
����A���̖_P������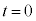 ��x���̕��̌����֑���v�őł��o�����B���̂��ƁA���̖_P�͎���
��x���̕��̌����֑���v�őł��o�����B���̂��ƁA���̖_P�͎���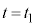 (
(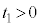 )��
)��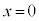 ��ʉ߂��Ď���̂���̈�֓������B�ȉ��ł́A����t �ɂ����铱�̖_P�̈ʒu�Ɠ��̖_�ɗ����d�����A���ꂼ��A
��ʉ߂��Ď���̂���̈�֓������B�ȉ��ł́A����t �ɂ����铱�̖_P�̈ʒu�Ɠ��̖_�ɗ����d�����A���ꂼ��A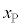 �C
�C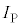 �Ƃ���B
�Ƃ���B
��5�@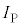 ��
��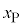 �̊W�ɂ��āA�ȉ��̕��͂̋ɓ���ׂ��������ɋL������B�������A���̖_P�ɍ�p����͂̐��̌�����x���̐��̌����Ƃ��A���̖_P�ɗ����d���̐��̌�����y���̐��̌����Ƃ���B
�̊W�ɂ��āA�ȉ��̕��͂̋ɓ���ׂ��������ɋL������B�������A���̖_P�ɍ�p����͂̐��̌�����x���̐��̌����Ƃ��A���̖_P�ɗ����d���̐��̌�����y���̐��̌����Ƃ���B ��ʂɁA����t ��������Ȏ���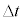 �����o�߂����Ƃ��̓d���Ɠ��̖_�̈ʒu�́A�d�ח�
�����o�߂����Ƃ��̓d���Ɠ��̖_�̈ʒu�́A�d�ח�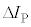 ��
��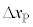 ��p���āA
��p���āA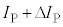 �C
�C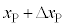 �ƕ\�����B
�ƕ\�����B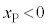 �̂Ƃ��A���ȗU���ɂ���ăR�C���ɐ�����N�d�͂Ǝ���̒����^�����铱�̖_P�ɐ�����U���N�d�͂��肠�����Ƃ���A
�̂Ƃ��A���ȗU���ɂ���ăR�C���ɐ�����N�d�͂Ǝ���̒����^�����铱�̖_P�ɐ�����U���N�d�͂��肠�����Ƃ���A 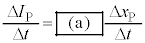 �@(1)
�@(1)�̊W��������B���̖_P������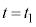 ��
��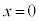 ��ʉ߂���Ƃ��ɂ�
��ʉ߂���Ƃ��ɂ�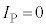 �ł��邽�߁A��(1)����A���̖_P�ɗ����d����
�ł��邽�߁A��(1)����A���̖_P�ɗ����d���� �ƂȂ�B���̓d��������邱�Ƃɂ�蓱�̖_P�ɂ�
�ƂȂ�B���̓d��������邱�Ƃɂ�蓱�̖_P�ɂ�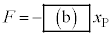 �̗͂��͂��炭�B���̗͂́A�˒萔��
�̗͂��͂��炭�B���̗͂́A�˒萔�� �̂˂ɂ�镜���͂Ƃ݂Ȃ����Ƃ��ł���B
�̂˂ɂ�镜���͂Ƃ݂Ȃ����Ƃ��ł���B 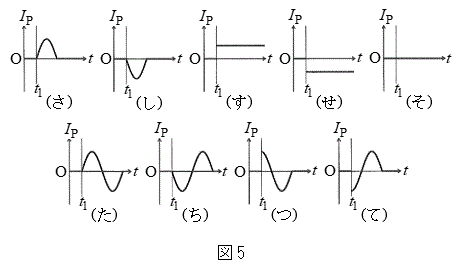 ��6�@���̖_P�ɗ����d��
��6�@���̖_P�ɗ����d��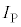 �̎��ԕω���}���������̂Ƃ��āA�ł��K�Ȃ��̂�}5��(��)����(��)�̒�����I��ŋL���œ�����B�������A���̖_P�ɗ����d���̐��̌�����y���̐��̌����Ƃ���B
�̎��ԕω���}���������̂Ƃ��āA�ł��K�Ȃ��̂�}5��(��)����(��)�̒�����I��ŋL���œ�����B�������A���̖_P�ɗ����d���̐��̌�����y���̐��̌����Ƃ���B
��7�@���̖_P�ɗ����d��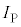 �̑傫���̍ő�l�����߂�B
�̑傫���̍ő�l�����߂�B
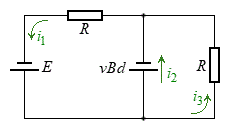
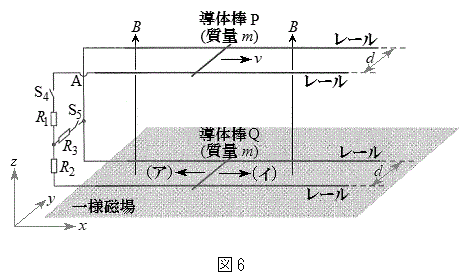 �U�D���ɁA�}6�Ɏ����悤�ɁA2�{�̃��[���Ɠ��̖_��2�g�ɑ��₵�A���ꂼ���z���W�̒l���قȂ鐅���ʓ��ɐݒu�����B�����āA�݂��̃��[�����X�C�b�`
�U�D���ɁA�}6�Ɏ����悤�ɁA2�{�̃��[���Ɠ��̖_��2�g�ɑ��₵�A���ꂼ���z���W�̒l���قȂ鐅���ʓ��ɐݒu�����B�����āA�݂��̃��[�����X�C�b�`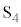 �C
�C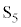 �C��R�l
�C��R�l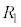 �C
�C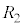 �C
�C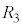 ������R�Ɠ�����p���Đڑ������B�����ł́A�㑤�ɂ��郌�[����̓��̖_��P�Ƃ��A�����̃��[����ɂ��铱�̖_��Q�Ƃ�ԁB�㉺�̃��[���Ɠ��̖_�́A�ǂ������l�Ȏ���̒��ɒu����Ă���B���̎������x�̑傫����B�ł���A����̌�����z���̐��̌����ł���B�������A�}6�ɋL��A�Ŏ������Ƃ���ł�2�{�̓����͐ڐG���Ă��Ȃ��B
������R�Ɠ�����p���Đڑ������B�����ł́A�㑤�ɂ��郌�[����̓��̖_��P�Ƃ��A�����̃��[����ɂ��铱�̖_��Q�Ƃ�ԁB�㉺�̃��[���Ɠ��̖_�́A�ǂ������l�Ȏ���̒��ɒu����Ă���B���̎������x�̑傫����B�ł���A����̌�����z���̐��̌����ł���B�������A�}6�ɋL��A�Ŏ������Ƃ���ł�2�{�̓����͐ڐG���Ă��Ȃ��B�͂��߂ɓ��̖_P��Q��Î~�����A�X�C�b�`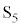 ���J�����܂܂ŃX�C�b�`
���J�����܂܂ŃX�C�b�`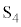 ������B���̌�A�O�͂������ē��̖_P��x���̐��̌����Ɉ��̑���v�œ��������B
������B���̌�A�O�͂������ē��̖_P��x���̐��̌����Ɉ��̑���v�œ��������B
��8�@���̖_P�����̑��x�œ������n�߂�����ɓ��̖_Q�ɍ�p����͂̌������A�}6�Ɏ�����(�A)�܂���(�C)�̋L���œ�����B�܂��A���̗͂̑傫�������߂�B
��9�@���̖_P�����̑��x�œ������n�߂Ă��炵�炭����ƁA���̖_Q�̑��x�͈��ɂȂ����B���̂Ƃ��̓��̖_Q�̑��������߂�B
��9�ɂ����ē��̖_Q�̑��x�����ɂȂ�����ɁA�X�C�b�`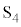 ������܂܂ŃX�C�b�`
������܂܂ŃX�C�b�`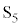 �������B�X�C�b�`
�������B�X�C�b�`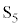 ���������A���̖_P��x���̐��̌����Ɉ��̑���v�œ������������B
���������A���̖_P��x���̐��̌����Ɉ��̑���v�œ������������B
��10�@�X�C�b�`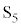 ���������ɒ�R�l
���������ɒ�R�l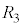 �̒�R�ɗ����d���̑傫�������߂�B
�̒�R�ɗ����d���̑傫�������߂�B ��11�@�X�C�b�`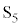 ����Ă��炵�炭����ƁA���̖_Q�̑��x�͈��ɂȂ����B���̂Ƃ��̓��̖_Q�̑��������߂�B
����Ă��炵�炭����ƁA���̖_Q�̑��x�͈��ɂȂ����B���̂Ƃ��̓��̖_Q�̑��������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���Ƃ͌����܂��A������N�d�͂̌����Ȃǐ����ɍׂ������ӂ��K�v�Ȗ��ł��B�U�D�͂܂Ƃ��ɂ��Ɖ�H�̘A���������������v�Z����ςł����A�T�D�̌o�����������āA�v�̂悭�v�Z���������̂ł��B�J���̂����l�Ȃ�A�J���œ����邱�Ƃ��ł������ł��B
�N�d�͂̌����́A���̖_P�ɏォ�牺�����ɓd���𗬂����Ƃ�������ł��B
��2�@���̖_P�ɗ����d���̑傫��I�́A�I�[���̖@�����A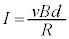 �C���̖_P�Ɏ��ꂪ�y�ڂ���(�t���~���O����̖@�����Q��)�̑傫���A�����A����Ƃ荇�����̖_P�ɉ����Ă���O�͂̑傫���́A
�C���̖_P�Ɏ��ꂪ�y�ڂ���(�t���~���O����̖@�����Q��)�̑傫���A�����A����Ƃ荇�����̖_P�ɉ����Ă���O�͂̑傫���́A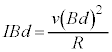 ......[��]
......[��]  �d�rE��y���������ɗ����d����
�d�rE��y���������ɗ����d����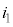 �C��R2��y���������ɗ����d����
�C��R2��y���������ɗ����d����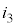 �C�܂��A���̖_P�̑��x��v�C�����x��a�C���̖_P(�N�d�͂͏オ���A������)��y���������ɗ����d����
�C�܂��A���̖_P�̑��x��v�C�����x��a�C���̖_P(�N�d�͂͏オ���A������)��y���������ɗ����d����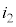 �Ƃ��܂��B�E�}���Q�Ƃ���ƁA�L���q�z�b�t��1�@�����A
�Ƃ��܂��B�E�}���Q�Ƃ���ƁA�L���q�z�b�t��1�@�����A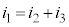 �@����@�L���q�z�b�t��2�@�����A�����̕�H�ɂ��āA
�@����@�L���q�z�b�t��2�@�����A�����̕�H�ɂ��āA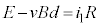 �@��
�@�� 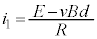 �E���̕�H�ɂ��āA
�E���̕�H�ɂ��āA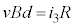 �@��
�@�� 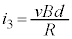 �@����A
�@����A
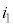 �C
�C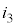 ���@�ɑ������ƁA
���@�ɑ������ƁA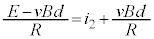 �@��
�@�� 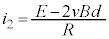 �@����B
�@����B���̖_P�ɓ����͂�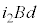 (
(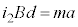 �Ȃ������x��������)�A
�Ȃ������x��������)�A
���̖_P���^���������́A 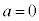 �@����C
�@����C
��3�@���̖_P�̑��x�����ɂȂ�Ƃ��A���̖_P�̉����x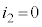
���̂Ƃ��A�C���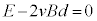 �C�B���A
�C�B���A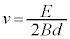 �@��
�@�� 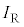 ......[��]
......[��]
��4�@��R2�ɗ����d��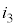 �́A��L��
�́A��L��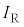 �̂��Ƃł��B�A������ƁA
�̂��Ƃł��B�A������ƁA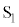 �͓��̖_P�̑��xv�Ɠ��l�̕ω������܂��B
�͓��̖_P�̑��xv�Ɠ��l�̕ω������܂��B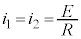 ����ē��̖_P�������n�߂�Ƃ��A
����ē��̖_P�������n�߂�Ƃ��A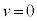 �ŁA�B���
�ŁA�B���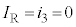 �C�A���
�C�A���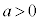 �C�C�ɂ�����
�C�C�ɂ�����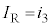 �œ��̖_P�̑��xv����������̂ɔ����A�A���
�œ��̖_P�̑��xv����������̂ɔ����A�A���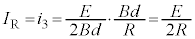 ������ɑ������܂��B���̖_P�̑��x�����ɂȂ�Ƃ��A��3�ƇA���A
������ɑ������܂��B���̖_P�̑��x�����ɂȂ�Ƃ��A��3�ƇA���A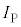 �ł��B���̂悤�ȕω������Ă���O���t�́A(��) ......[��]
�ł��B���̂悤�ȕω������Ă���O���t�́A(��) ......[��]
��5�@���̖_P�����ꒆ(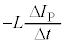 )��x���������Ɉړ�����Ƃ��A���̖_P�ɂ͉����������̋N�d�͂��������܂��B���̖_P��y���������ɗ����d��
)��x���������Ɉړ�����Ƃ��A���̖_P�ɂ͉����������̋N�d�͂��������܂��B���̖_P��y���������ɗ����d��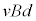 ���R�C��L�ɗ��ꍞ��ő��傷��ƁA�R�C���ɂ�y���������̋t�N�d��
���R�C��L�ɗ��ꍞ��ő��傷��ƁA�R�C���ɂ�y���������̋t�N�d��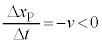 �������܂�(���ȗU�����Q��)�B���̖_P�ɋN�d��
�������܂�(���ȗU�����Q��)�B���̖_P�ɋN�d��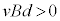 ��������(�����ɒ��ӁB�t���~���O�E��̖@�����N�d�͂�y���������ł����A���̖_P��x���������ɑ���v�œ����Ƃ�
��������(�����ɒ��ӁB�t���~���O�E��̖@�����N�d�͂�y���������ł����A���̖_P��x���������ɑ���v�œ����Ƃ�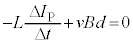 �ł���A�N�d��
�ł���A�N�d��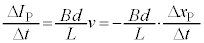 �ł�)�̂ŁA�L���q�z�b�t��2�@�����A
�ł�)�̂ŁA�L���q�z�b�t��2�@�����A 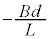 �@��
�@�� 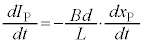 �@���(1)�@
�@���(1)�@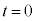 ......[(a)]
......[(a)](1)��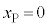 �Ƃ݂Đϕ����A
�Ƃ݂Đϕ����A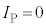 �̂Ƃ�
�̂Ƃ�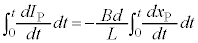 �C
�C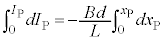 �ł��邱�Ƃ��l������ƁA
�ł��邱�Ƃ��l������ƁA ���̖_P��x���������ɓ����Ƃ��A���̖_P��y���������̋N�d�͂������ēd��������Ax���������ɓ�����F�́A�D���A
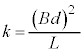 �@
�@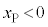 ......[(b)]
......[(b)]
��6�@��5�̓��̖_�ɓ�����F���A�˒萔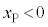 �̂˂ɂ�镜���͂Ƃ݂Ȃ��ƁA���̖_P��
�̂˂ɂ�镜���͂Ƃ݂Ȃ��ƁA���̖_P��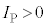 �ɂ����āA�P�U���̔��������̉^�������܂��B���̊ԁA�D���A���̖_P�ɂ�y��������(��5[(b)]�ɂ�����
�ɂ����āA�P�U���̔��������̉^�������܂��B���̊ԁA�D���A���̖_P�ɂ�y��������(��5[(b)]�ɂ�����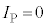 �Ȃ̂�
�Ȃ̂�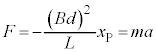 �ł�)�̐U���d��������܂��B�P�U�����������̉^����A���̖_P��x���������̑��x�������Ă���̂ŁA���ꂩ��e��������x���������ɓ����x�^���𑱂��A�N�d�͂͂Ȃ��Ȃ�A
�ł�)�̐U���d��������܂��B�P�U�����������̉^����A���̖_P��x���������̑��x�������Ă���̂ŁA���ꂩ��e��������x���������ɓ����x�^���𑱂��A�N�d�͂͂Ȃ��Ȃ�A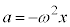 �ƂȂ�܂��B���̂悤�ɂȂ��Ă���O���t�́A(��) ......[��]
�ƂȂ�܂��B���̂悤�ɂȂ��Ă���O���t�́A(��) ......[��]
��7�@��5[(b)]�ɂ��ƒP�U�����Ă���Ԃ̉^���������́A���̖_P�̉����x��a�Ƃ��āA
�p�U������ω�Ƃ��āA�P�U���̌����F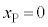 ���A
���A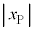
�P�U�����n�܂����u��(�U�����S��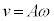 )�̓��̖_�̑���v���P�U���̑����̍ő�l�ł��B
)�̓��̖_�̑���v���P�U���̑����̍ő�l�ł��B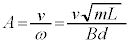 �̍ő�l�͒P�U���̐U��A�ɓ������A�P�U���̌������A
�̍ő�l�͒P�U���̐U��A�ɓ������A�P�U���̌������A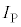 �C
�C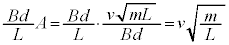
�D��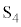 �Ƃ��āA�d��
�Ƃ��āA�d��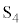 �̑傫���̍ő�l�́A
�̑傫���̍ő�l�́A 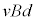 ......[��]
......[��]
�U�D��8�@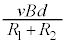 ����ē��̖_P��x���������ɓ����n�߂�����A�t���~���O�E��̖@�����A���̖_P�ɂ�y���������̋N�d�͂��������A���̋N�d�͂ɂ��A
����ē��̖_P��x���������ɓ����n�߂�����A�t���~���O�E��̖@�����A���̖_P�ɂ�y���������̋N�d�͂��������A���̋N�d�͂ɂ��A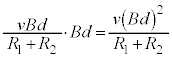 ����z���������ɓd��������܂��B���̓d�������̖_Q��y���������ɗ���A�t���~���O����̖@�����x���������̗͂����ꂩ��܂��B�@(�C) ......[��]
����z���������ɓd��������܂��B���̓d�������̖_Q��y���������ɗ���A�t���~���O����̖@�����x���������̗͂����ꂩ��܂��B�@(�C) ......[��] ���̂Ƃ��A���̖_P�ɔ�������N�d�͂̑傫����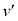 �ł��B���̖_Q�ɗ����d���̓I�[���̖@�����A
�ł��B���̖_Q�ɗ����d���̓I�[���̖@�����A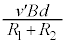 �ł��B���̖_Q�ɓ����͂̑傫���́A
�ł��B���̖_Q�ɓ����͂̑傫���́A 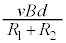 ......[��]
......[��]
��9�@���̖_Q��x���������̗͂������̂ŁA���̖_Q��x���������ɓ����n�߂܂��B�����n�߂���A���̖_Q�̑�����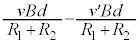 �Ƃ���ƁA���̖_Q��y���������̋N�d�͂��܂��B���̋N�d�͂ɂ���ē��̖_Q�ɗ����d����y���������ɑ傫��
�Ƃ���ƁA���̖_Q��y���������̋N�d�͂��܂��B���̋N�d�͂ɂ���ē��̖_Q�ɗ����d����y���������ɑ傫��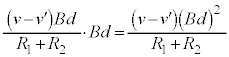 �ŁC���̖_Q�ɗ����d���́A���̖_P�ɔ�������N�d�͂ɂ��d��
�ŁC���̖_Q�ɗ����d���́A���̖_P�ɔ�������N�d�͂ɂ��d��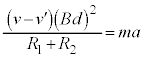 (���̖_Q��y���������ɗ���܂�)�ƍ��킹�āA
(���̖_Q��y���������ɗ���܂�)�ƍ��킹�āA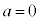 �C���̓d�������ꂩ���͂́A
�C���̓d�������ꂩ���͂́A ���̖_Q�̉^���������́A�����x��a�Ƃ��āA
���̖_Q�̑��x�����ɂȂ�Ƃ��A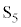 �Ȃ̂ŁA
�Ȃ̂ŁA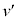 ......[��]
......[��]
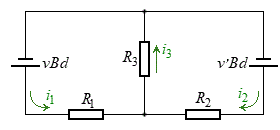 ��10�@���̖_Q�̑��x�����ɂȂ�����ɁA
��10�@���̖_Q�̑��x�����ɂȂ�����ɁA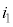 ������܂܂�
������܂܂�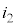 ����A���̖_P��x�����̌����Ɉ��̑���v�œ������������Ƃ��A���̖_Q�̑��x��
����A���̖_P��x�����̌����Ɉ��̑���v�œ������������Ƃ��A���̖_Q�̑��x��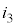 ���Ƃ��āA��H�̏��E�}�Ɏ����܂��B���̖_P�ɔ�������N�d�́A���̖_Q�ɔ�������N�d�́A�Ƃ��Ɍ�����y���������ł��B�d��
���Ƃ��āA��H�̏��E�}�Ɏ����܂��B���̖_P�ɔ�������N�d�́A���̖_Q�ɔ�������N�d�́A�Ƃ��Ɍ�����y���������ł��B�d��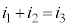 �C
�C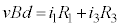 �C
�C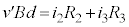 ���E�}�̂悤�ɒ�߂�ƁA
���E�}�̂悤�ɒ�߂�ƁA�L���q�z�b�t��1�@�����A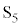 �@����E
�@����E
�L���q�z�b�t��2�@�����A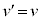 �@����F
�@����F 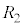 �@����G
�@����G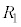 ���������ɂ͖�9���
���������ɂ͖�9���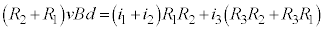 �Ƃ��āA�F�~
�Ƃ��āA�F�~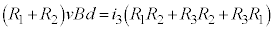 �{�G�~
�{�G�~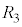 ���A
���A�E���A
����āA��R�l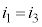 �̒�R�ɗ����d���̑傫���́A
�̒�R�ɗ����d���̑傫���́A 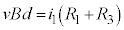 ......[��]
......[��]
��11�@��3�C��9�Ɠ��l�ɁA���̖_Q�̑��x�����ɂȂ�Ƃ��A���̖_Q�̉����x��0�ŁA���̖_Q�ɓ����͂�0�ł��B���̂��߂ɂ́A���̖_Q�ɗ����d����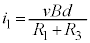 �ƂȂ�܂��B�E���
�ƂȂ�܂��B�E���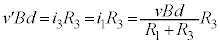 �C�F���
�C�F���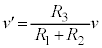 �C
�C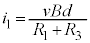 �C�G���A
�C�G���A 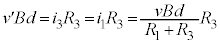 �@��
�@�� 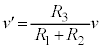 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 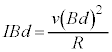 ......[��]
......[��]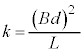 �@
�@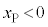 ......[(b)]
......[(b)]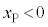 �̂˂ɂ�镜���͂Ƃ݂Ȃ��ƁA���̖_P��
�̂˂ɂ�镜���͂Ƃ݂Ȃ��ƁA���̖_P��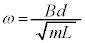
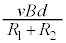 ......[��]
......[��]