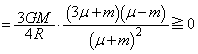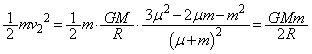���啨��'13�N[1]
���̕��͂�ǂ�ŁA�@�@�ɓK���������A���ꂼ��̉��ɋL������B�Ȃ��A�@�@�͂��ł��@�@�ŗ^����ꂽ���̂Ɠ�������\���B�܂��A��1�C��2�ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B
�ȉ��̐ݖ�ł́A�n���͔��aR�̋��ł���A���x�͈�l�ɕ��z���Ă���ƍl���Ă悢�B�܂��A�n���̎��ʂ�M�C���L���͒萔��G�Ƃ��A�n���̎��]�̉e���A���C�A����ы�C�̒�R�͖������̂Ƃ���B
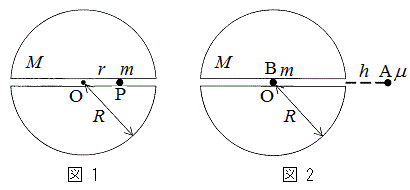 (1) �}1�̂悤�ɁA�n���̒��SO��ʂ��Ē�����Ɍ@��ꂽ�g���l�����l����B�g���l���͏\���ɍׂ��A�g���l�����@�������Ƃɂ�鎿�ʂ̕ω��͖����ł�����̂Ƃ���B�g���l�����̔C�ӂ�1�_P (
(1) �}1�̂悤�ɁA�n���̒��SO��ʂ��Ē�����Ɍ@��ꂽ�g���l�����l����B�g���l���͏\���ɍׂ��A�g���l�����@�������Ƃɂ�鎿�ʂ̕ω��͖����ł�����̂Ƃ���B�g���l�����̔C�ӂ�1�_P (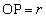 )�Ŏ���m�̎��_�ɓ����d�͂́AO�𒆐S�Ƃ������ar�̋��̎��ʂ����SO�ɏW�܂����Ƃ��āA����Ǝ��_�Ƃ̊Ԃ̖��L���͂ɓ������A���ar�̋��̊O���̕����́A���̓_�ł̏d�͂ɂ͖��W�ł��邱�Ƃ��m���Ă���B���������āA�g���l������1�_P�ɂ����Ď��_�ɓ����d�͂̑傫���́Am�CM�CR�Cr�CG���g�����@�A�@�ƕ\�����Ƃ��ł���B���̗͂ɂ�鎿�_�̉^���͒P�U���ł���A���̎������@�C�@�ŗ^������B
)�Ŏ���m�̎��_�ɓ����d�͂́AO�𒆐S�Ƃ������ar�̋��̎��ʂ����SO�ɏW�܂����Ƃ��āA����Ǝ��_�Ƃ̊Ԃ̖��L���͂ɓ������A���ar�̋��̊O���̕����́A���̓_�ł̏d�͂ɂ͖��W�ł��邱�Ƃ��m���Ă���B���������āA�g���l������1�_P�ɂ����Ď��_�ɓ����d�͂̑傫���́Am�CM�CR�Cr�CG���g�����@�A�@�ƕ\�����Ƃ��ł���B���̗͂ɂ�鎿�_�̉^���͒P�U���ł���A���̎������@�C�@�ŗ^������B
(2) ���ɁA�}2�̂悤�ɁA�g���l����ʂ钼���ɉ����āA�n�\����̍�����h�̓_�Ɏ���μ�̎��_A��Â��ɒu���A�Î~������Ԃ���g���l���ɗ��������A���SO�ɐÎ~���Ă��鎿��m�̎��_B�ɏՓ˂�����B���_A���g���l���ɓ���u�Ԃ̑������@�E�@�ŁA���SO�ɓ��B���钼�O�̑������@�G�@�ł���B�Փ˂͒e���Փ˂ł���Ƃ���ƁA�Փ˒���̎��_A�̑������@�I�@�C���_B�̑������@�J�@�ƂȂ�B�Փˌ�A���_B�͔��Α��̒n�\�ɒB�����B
��1�@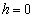 �Ƃ����ꍇ�ɁA���̌㎿�_B�������̉����ɔ�ы��邽�߂ɕK�v��
�Ƃ����ꍇ�ɁA���̌㎿�_B�������̉����ɔ�ы��邽�߂ɕK�v��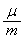 �̒l�͈̔͂����߂�B���o�̉ߒ������킹�Ď����B
�̒l�͈̔͂����߂�B���o�̉ߒ������킹�Ď����B
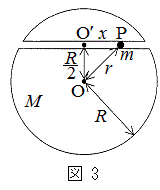 (3) ���x�́A�}3�̂悤�ɁA�n���̒��SO����
(3) ���x�́A�}3�̂悤�ɁA�n���̒��SO����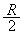 �������ꂽ�Ƃ����ʂ钼����ׂ̍��g���l�����@�����B���SO����̋�����r�ŁA�g���l���̒��S
�������ꂽ�Ƃ����ʂ钼����ׂ̍��g���l�����@�����B���SO����̋�����r�ŁA�g���l���̒��S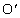 ����x�������ꂽ�g���l������P�_�ɂ��鎿��m�̎��_�ɓ����d�͂̑傫�����@�A�@�Ȃ̂ŁA���̎��_�ɓ����g���l���ɉ����������̗͂̑傫���́Am�CM�CR�Cx�CG���g�����@�L�@�ŗ^������B���������āA�n�\�ŐÎ~������Ԃ���g���l����ʂ��Ĕ��Α��̒n�\�ɏo��܂łɂ����鎞�Ԃ��@�N�@�ł���B
����x�������ꂽ�g���l������P�_�ɂ��鎿��m�̎��_�ɓ����d�͂̑傫�����@�A�@�Ȃ̂ŁA���̎��_�ɓ����g���l���ɉ����������̗͂̑傫���́Am�CM�CR�Cx�CG���g�����@�L�@�ŗ^������B���������āA�n�\�ŐÎ~������Ԃ���g���l����ʂ��Ĕ��Α��̒n�\�ɏo��܂łɂ����鎞�Ԃ��@�N�@�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���w�̎������̊ȒP���ɔ�ׂāA�����̕��G���͉��Ȃ̂��A�ƁA���������Ȃ�܂����A�����͎��I�ɂ��ʓI�ɂ��{�����[�����_�Ŏ��ԓ��ɂ�肫��͍̂���ł��傤�B
�{��́A�n�\����O���Ɠ����Ƃ��ʒu�G�l���M�[�̍l������ς���K�v������Ƃ��낪�|�C���g�ɂȂ��Ă��܂��B(2)(�G)�A(3)(�P)�ŔY�݂܂����A(1)�Ńg���l�����Ŏ��_���P�U�����邱�Ƃ��肪����Ƃ��čl���܂��傤�B
(1) ���ar�̋����̐���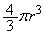 �C���aR�̋����̐���
�C���aR�̋����̐���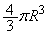 �C�n����������M�ł��邱�Ƃ���A�n�������x��ρ�Ƃ��āA
�C�n����������M�ł��邱�Ƃ���A�n�������x��ρ�Ƃ��āA 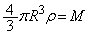 �@��
�@�� 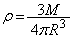
O�𒆐S�Ƃ������ar�̋��������́A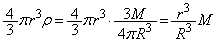
���_�ɓ����d���̑傫���́A���L���͂̌������A (�A) 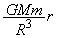 ......[��]�d���̌�����r����������������ŁA���_�������x��a�Ƃ��āA���_���^���������́A
......[��]�d���̌�����r����������������ŁA���_�������x��a�Ƃ��āA���_���^���������́A �� 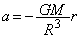 ����́A���_���p�U����
����́A���_���p�U����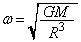 �̒P�U�����s�����Ƃ������܂��B�P�U��������T�́A
�̒P�U�����s�����Ƃ������܂��B�P�U��������T�́A (�C) 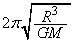 ......[��]
......[��]
(2) ����h�̓_�ł��ʒu�G�l���M�[�́A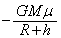
�n�\�ł��ʒu�G�l���M�[�́A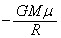 �C�g���l���ɓ���u�Ԃ�������v�Ƃ��āA�^���G�l���M�[�́A
�C�g���l���ɓ���u�Ԃ�������v�Ƃ��āA�^���G�l���M�[�́A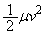
���n�_�ł��͊w�I�G�l���M�[�ۑ����A 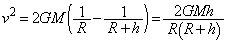 �@��
�@�� 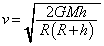 (�E)
(�E) 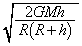 ......[��]
......[��]
(1)�Ō����悤�ɁA���_�̓g���l���ɓ���ƁA�p�U����ω �̒P�U�������܂��B������A�o�l�萔k�̃o�l�U��q�Ɠ��l�ɍl���A�ʒu�G�l���M�[��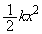 �ƍl����ƁA(�A)�̌��ʂ��
�ƍl����ƁA(�A)�̌��ʂ��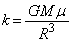 �Ƃ��邱�Ƃɂ��A�n���̒��S��������r�̒n�_�ɂ��鎿�_A���ʒu�G�l���M�[�́A
�Ƃ��邱�Ƃɂ��A�n���̒��S��������r�̒n�_�ɂ��鎿�_A���ʒu�G�l���M�[�́A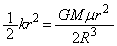
�g���l���ɓ���u��( )���ʒu�G�l���M�[�́A
)���ʒu�G�l���M�[�́A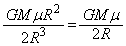
�g���l���̒��S�ɓ��B���钼�O�̎��_A��������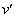 �Ƃ��āA�g���l���ɓ���u�Ԃƃg���l���̒��S�Ƃ��͊w�I�G�l���M�[�ۑ����A
�Ƃ��āA�g���l���ɓ���u�Ԃƃg���l���̒��S�Ƃ��͊w�I�G�l���M�[�ۑ����A(�E)�̌��ʂ�p���āA
�� 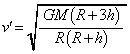
(�G) 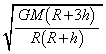 ......[��]�Փ˒���̎��_A�C���_B�����x�����ꂼ��A
......[��]�Փ˒���̎��_A�C���_B�����x�����ꂼ��A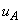 �C
�C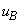 �Ƃ���ƁA�ՓˑO����^���ʕۑ����A
�Ƃ���ƁA�ՓˑO����^���ʕۑ����A 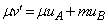 �@����@
�@����@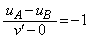 �@����A
�@����A�A���A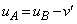 �C������@�ɑ�����āA
�C������@�ɑ�����āA �� 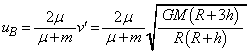
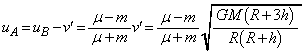 �@(���_A��������
�@(���_A��������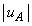 )
)(�I) 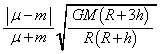 �C(�J)
�C(�J) 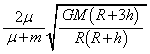 ......[��]
......[��]
��1�@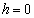 �̂Ƃ��A
�̂Ƃ��A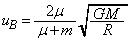 �ł��B���̂Ƃ��A�n�\�ɒB�����Ƃ��̎��_B��������
�ł��B���̂Ƃ��A�n�\�ɒB�����Ƃ��̎��_B��������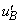 �Ƃ��āA�Փ˒���ƒn�\�ɒB�����Ƃ�(�ʒu�G�l���M�[�́A(�G)�Ɠ��l�ɍl����
�Ƃ��āA�Փ˒���ƒn�\�ɒB�����Ƃ�(�ʒu�G�l���M�[�́A(�G)�Ɠ��l�ɍl����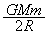 )�Ƃ��͊w�I�G�l���M�[�ۑ����A
)�Ƃ��͊w�I�G�l���M�[�ۑ����A ���������ł̎��_B��������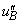 �Ƃ��āA���������ƒn�\�Ƃ��͊w�I�G�l���M�[�ۑ����A
�Ƃ��āA���������ƒn�\�Ƃ��͊w�I�G�l���M�[�ۑ����A
(3) ���_���_P�ɂ���Ƃ��A�n���̒��SO�Ƃ�������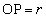 �Ƃ��āA���_�ɓ����d��
�Ƃ��āA���_�ɓ����d��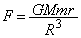 �̃g���l���ɉ����������̐����̑傫���́A
�̃g���l���ɉ����������̐����̑傫���́A (�L) 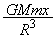 ......[��]
......[��]
(�L)�̌�����x����������������ŁA�����x��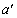 �Ƃ��āA�^���������́A
�Ƃ��āA�^���������́A �� 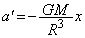 ����́A���_���p�U����
����́A���_���p�U����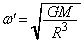 �̒P�U�����s�����Ƃ��Ӗ����܂��B
�̒P�U�����s�����Ƃ��Ӗ����܂��B
�n�\�ŐÎ~������Ԃ���g���l����ʂ��Ĕ��Α��̒n�\�ɏo��܂łɂ����������́A�P�U��������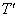 ��
��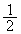 �ŁA
�ŁA (�N) 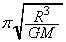 ......[��]
......[��]
(4) (3)�̒P�U�����U���́A�ŏ��A�n�\�ŐÎ~���Ă����̂ŁA�g���l���̒[�_�ƒ��S�Ƃ������ɓ������A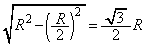 �ł��B
�ł��B (�I)(�J)�Ɠ��l�ɂ��āA�Փ˒����B�����x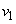 �́A
�́A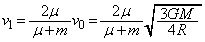 (�G)�Ɠ��l�ɂ��āA�o�l�U��q����̗ސ����ʒu�G�l���M�[���l���܂��B�����x��
(�G)�Ɠ��l�ɂ��āA�o�l�U��q����̗ސ����ʒu�G�l���M�[���l���܂��B�����x��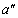 �Ƃ��āA�^���������́A
�Ƃ��āA�^���������́A �ƂȂ�̂ŁA�o�l�萔��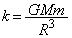 �Ƃ��āA�ʒu�G�l���M�[�́A
�Ƃ��āA�ʒu�G�l���M�[�́A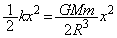 �C�g���l���̒[�_�ł́A
�C�g���l���̒[�_�ł́A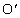 �Ƃ�������
�Ƃ�������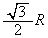 �Ȃ̂ŁA
�Ȃ̂ŁA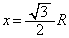 �̂Ƃ��A
�̂Ƃ��A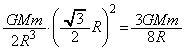 �ƂȂ�܂��B
�ƂȂ�܂��B
��1�Ɠ��l�ɂ��āA�n�\�ɒB�����Ƃ��̎��_B��������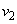 �Ƃ��āA�Փ˒���ƒn�\�ɒB�����Ƃ��Ƃ��͊w�I�G�l���M�[�ۑ����A
�Ƃ��āA�Փ˒���ƒn�\�ɒB�����Ƃ��Ƃ��͊w�I�G�l���M�[�ۑ����A �� 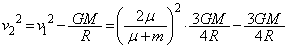
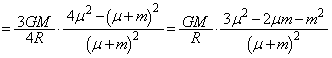 �@����@
�@����@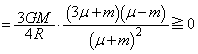
���A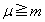 (�P) m ......[��]
(�P) m ......[��]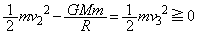 �ł���A���_�͒n���̈��͌���E���Ė������ɔ�ы����Ă��܂��̂ŁA�߂��Ă��邽�߂ɂ́A
�ł���A���_�͒n���̈��͌���E���Ė������ɔ�ы����Ă��܂��̂ŁA�߂��Ă��邽�߂ɂ́A �� 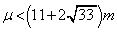 (�R)
(�R) 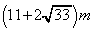
��2�@��蕶���n�\�ł��^���G�l���M�[��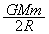 �ł��邱�Ƃ���A�@���A
�ł��邱�Ƃ���A�@���A �� 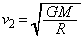 �n�\�����яo���u�Ԃ��͊w�I�G�l���M�[�́A
�n�\�����яo���u�Ԃ��͊w�I�G�l���M�[�́A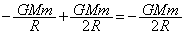
�n������ł����ꂽ�n�_�ƒn���̒��S�Ƃ�������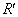 �C�����ł̎��_B��������
�C�����ł̎��_B��������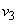 �Ƃ���ƁA�͊w�I�G�l���M�[�ۑ����A
�Ƃ���ƁA�͊w�I�G�l���M�[�ۑ����A 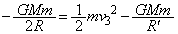 �@��
�@�� 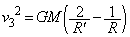
�n�\�����яo���Ƃ��A��яo���n�_�ƒn���̒��S�����Ԓ����ƁA�g���l�������A�����A���_B�����x�Ƃ̂Ȃ��p��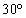 �ł��B�ʐϑ��x�́A�n�\�����яo���Ƃ��A
�ł��B�ʐϑ��x�́A�n�\�����яo���Ƃ��A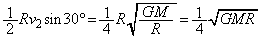 �C�ł����ꂽ�Ƃ��A
�C�ł����ꂽ�Ƃ��A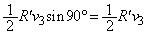 �C�ʐϑ��x�����A
�C�ʐϑ��x�����A
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 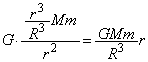
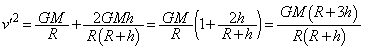
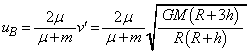
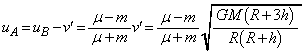 �@(���_A��������
�@(���_A��������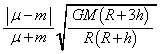 �C(�J)
�C(�J) 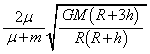 ......[��]
......[��]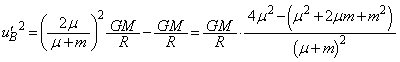
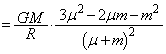
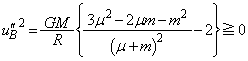
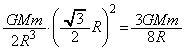 �ƂȂ�܂��B
�ƂȂ�܂��B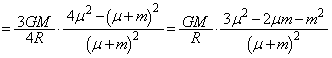 �@����@
�@����@