���H�啨�� '11 �N�O�� [1] �} 1 �̂悤�ɐL�яk�݂��Ȃ��y�����ɂ�����Ƃ��ď����ȋʂ������U��q�� 2 �p�ӂ��A 2 �̂����肪���ꂼ��̍ʼn��_�ɂ����ē��������ō��E�ɐڐG����悤�ɔz�u����B������U��q 1 �C�E����U��q 2 �Ƃ���B�U��q 1 �C�U��q 2 �̂���������ꂼ�ꂨ���� 1 �C������ 2 �Ƃ��A�d�͉����x�� g �Ƃ���B 2 �̂�����͐}�̎��ʓ��ł̂݉^������B 2 �̐U��q�͂����肪�Փ˂���ȊO�A�݂��Ɋ����Ȃ��B�U��q�̐U��͏\���������A�U��q�̓����������藧�Ƃ���B��C��R�͖�������B [A] �@�܂��A 2 �̐U��q�̎��̒������ǂ���� L �ł���ꍇ ( �} 2(i)) ���l����B������ 1 �C������ 2 �̎��ʂ����ꂼ�� 2 �̂�����̊Ԃ̂͂˕Ԃ�W���� e (�Ƃ���B �����̂��������������܂Ȃ��悤�ɍ��E�Ɉ��������A�ʼn��_���炻�ꂼ�ꓯ������ h ���������グ ( �} 2(ii)) �Â��ɕ����ƁA 2 �̂�����͍ʼn��_�ɂ����ďՓ˂��J��Ԃ����B
(a) �����������Ă���ŏ��ɏՓ˂���܂ł̎��� (b) 1 �x�ڂ̏Փ˂̒��O�̂����� 1 �̑��� v �����߂�B
(c) 1 �x�ڂ̏Փ˂̒���̂����� 1 �Ƃ����� 2 ���ꂼ��̑��x 2(ii) �Ɏ����悤�ɉE�����𐳁A�������Ƃ���B�ɂ� v ��p���Ă悢�B (d) 4 �x�ڂ̏Փ˂̒���̂����� 1 �Ƃ����� 2 ���ꂼ��̑��x (c) �Ɠ��l�ɒ�`����B�ɂ� v ��p���Ă悢�B [B] �@���ɁA�U��q 1 �̎��̒����� [A] �Ɠ��� L �̂܂܂ɕۂ��A�U��q 2 �͂��̎������U��q 1 �� 2 �{�ɂȂ�悤�Ɏ��� ( �} 3(i)) �B����ɁA 2 �̂�������݂��ɒe���Փ� ( ������̂Ɏ��ւ����B������ 1 �Ƃ�����̎��ʂ� 2 ���ʼn��_�ŐÎ~���Ă����ԂŁA������ 1 ��������������܂Ȃ��悤�ɍ����ɓ������čʼn��_���炠�鍂���܂Ŏ����グ ( �} 3(ii)) �A���� 2 �̂�����͂��̌�A�ʼn��_�݂̂ʼn��Փ˂��A ( �ɉ^�����J�n�����Ƃ��̏�� ) �ɖ߂����B������ (a) �ŋ��߂����Ԃł���B (e) ���� 1 ������Ă���A 2 �̂����肪���̏�Ԃɖ߂�܂ł̊ԂɁA 2 �̂����肪�Փ˂���������S�ċ�����B�ɂ� (f) ������̎��ʂ̔�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�� �@�P���ȌJ��Ԃ� �Փ� �̖��ł����A�w�^�Ɍv�Z��i�߂�Ƃ�����ł���ςɂȂ��Ă��܂��܂��B�S�e�𑨂��Ă���v�Z�̕��j�𗧂Ă�悤�ɂ��܂��傤�B [A](a) �P�U��q �� ���� �̌������A�U��q�� ���� T �́A ���� �́A ���� �ɑ������A ......[ �� ] (b) ������ 1 ������Ƃ��A������ 1 �́A �d�� �� �ʒu�G�l���M�[ �������Ă��܂��B�ʼn��_�ɗ����Ƃ��A�Փ˂̒��O�ɁA������ 1 �́A �^���G�l���M�[ �������Ă��܂��B���҂� �͊w�I�G�l���M�[�ۑ� ���A �@�� �� ] (c) �Փ˒��O�� �^���� �́A������ 1 �� 2 �� �^���� �́A������ 1 �� 2 �� �^���ʕۑ� ���A �@����@ �@����A �@�ɑ�����āA
�� �� ] �A�ɑ�����āA ......[ �� ] (d) 2 ��ڂ̏Փ˒��O�̂����� 1 �C������ 2 �� ���x �́A 2 ��ڂ̏Փ˒���̂����� 1 �C������ 2 �� ���x ���^���ʕۑ� ���A �����W���̎�
�@����B �������� 3 ��ڂ̏ՓˁA 4 ��ڂ̏ՓˁA�Ƃ���Ă����Ƒ�ςȂ��ƂɂȂ�܂��B�B�̕���́A �@����C �ƂȂ�܂��B 3 ��ڂ̏Փ˒��O�̂����� 1 �C������ 2 �� ���x �́A 3 ��ڂ̏Փ˒���̂����� 1 �C������ 2 �� ���x ���^���ʕۑ� ���A �����W���̎�
2 ��ڂ̏Փ˂̂Ƃ��Ɠ��l�ɁA�C��p���āA
����ŁA �^���� �̑��a�̕��́A�Փ˒��ォ�玟�̏Փ˒��O�܂łŐ������]���邾���ł��B ���x �̕����̐ݒ����蒼���A n ��ڂ̏Փ˒���̂����� 1 �C������ 2 �� ���x �� n ��ڂ̏Փ˂ɂ��čl���邱�Ƃɂ��܂��B������ 1 �C������ 2 �� 1 ��ڂ̏Փ˒��O�� ���x �́A v �C 0 ��ڂ̏Փ˒���̂����� 1 �C������ 2 �� ���x �C n ��ڂ̏Փ˒��O�́A������ 1 �C������ 2 �� ���x �́A n ��ڂ̏ՓˑO����^���ʕۑ� ���A �@����D �����W���̎�
�@����E �D�C�E�������A���� �A���Q���� �ƍl���܂��B�D���A ������A ���䐔�� �ł��B �@����F ������A e �̓��䐔��ł��B �F�ɁA �C ......[ �� ] [B](e) �U��q 1 �� [A] �Ɠ����Ȃ̂ŁA�ʼn��_�ŏՓ˂���̂ł���A 1 ��ڂ̏Փ˂� 1 ��ڂ̏Փ˒��O�̂����� 1 �� ���x �� V (�C n ��ڂ̏Փ˒���̂����� 1 �A������ 2 �� ���x �� 1 ��ڂ̏ՓˑO����^���ʕۑ� ���A �@����G �����W���̎�
�G�ɑ�����āA
�� �C 1 ��ڂ̏Փˌ�̂����� 1 �̉^�������ɂ���ĈȌ�̉^�����ς��܂��B (i) �̂Ƃ��A [A](a) ��肨���� 1 �� ���� �� 2 �� ���� �� 2 �� ������ ��ʼn��_�ɂ����āA 2 ��ڂ̏Փ˂� 2 ��ڂ̏Փ˒���A 1 �� ������ ��ʼn��_�ɂ����� 3 ��ڂ̏Փ˂� 3 ��ڂ̏Փ˒���A 2 �� ������ ��ʼn��_�ɂ����� 4 ��ڂ̏Փ˂� 1 ����~���Ă��āA���̏�Ԃɖ߂�܂���B (ii) �̂Ƃ��A 1 ��ڂ̏Փˌ�A������ 1 �͍��ցA������ 2 �͉E�֓����܂��B������ 1 �� 2 �͍ł��E���ɍs���Ă��܂��B�����肪�ʼn��_�݂̂ŏՓ˂���A�Ƃ������Ƃ́A���̎��_���炳��ɂ����� 1 �� ������ ( ������ 2 �� ���� ) �� 2 ��ڂ̏Փ˂��N����A�Ƃ������Ƃł��B 2 ��ڂ̏Փ˒��O�ɁA������ 1 �C������ 2 �Ƃ��ɍ������ɁA ���x �C 2 �̕��� ���� ���傫���A �� �̂Ƃ��ɂ́A������ 1 �C������ 2 �Ƃ��ɍʼn��_�̍����ɐi�݁A������ 2 �� ���� �̕��������̂ŁA�ʼn��_�̍����ŏՓ˂��Ă��܂����ƂɂȂ�܂��B 2 ��ڂ̏ՓˑO����^���ʕۑ� ���A �����W���̎� �F
�C
�ɂ��ĉ����ƁA
�C �Ȃ̂ŁA 2 ��ڂ̏Փˌ�A 2 �̂�����́A�Ƃ��ɍ����֓����܂��B������ 2 �� ���� �̕��������̂ŁA�ʼn��_�̍����ŏՓ˂��Ă��܂����ƂɂȂ�A���̏ꍇ���s�K�ł��B (iii) �̂Ƃ��A 1 ��ڂ̏Փˌ�A 2 �̂�����͂Ƃ��ɁA�E���֓����܂��B������ 1 ���ʼn��_�ɖ߂�Ƃ��A������ 2 �͍ł��E���ɍs���Ă��܂��B������ 1 ���A��U���֍s���ʼn��_�ɖ߂�Ƃ��A������ 2 ���ʼn��_�ɗ��āA�ʼn��_�ŏՓ˂��܂��B 2 ��ڂ̏Փ˂� 2 ��ڂ̏Փ˒��O�ɁA������ 1 �C������ 2 �� ���x �́A 2 ��ڂ̏Փˌ�A������ 2 �͉E���֓����܂��B���̂Ƃ��A������ 1 ���Փˌ�ɂǂ���ɓ����Ă��A�ʼn��_�� 3 ��ڂ̏Փ˂��N����̂ł���A������ 2 �� ������ ��A �ȏ���A 2 �̂����肪�Փ˂��� ���� �́A ......[ �� ] (f) (e)(iii) �̏ꍇ�ɁA 3 ��ڂ̏Փ˒��O�̂����� 1 �C������ 2 �� ���x �� 3 ��ڂ̏ՓˑO����^���ʕۑ� ���A
�@����I �� �@ ( �� �H ) �� �C ......[ �� ]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@ ���H�啨�� TOP �@�@ ���� TOP �@�@ TOP �y�[�W�ɖ߂� �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B �e���̒��쌠�� © 2005-2024 (�L)����� ��w�y�w�m ���������t���I ���n��w�l�b�g�m ��w�y�w�m (���ē��������� )������́A������܂Ń��[�� �� 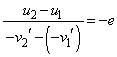 �@����B
�@����B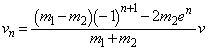 �C
�C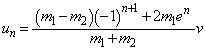
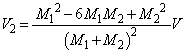 �C
�C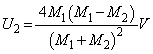 �@����H
�@����H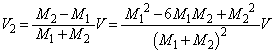 �@(�� �H)
�@(�� �H)