ÈwåHwn¨'25NOú[3]
\ªÈ·³ðÂV_[àɿʪ³Å«ésXgª èA»êçÉæè¶ßçê½CÌÌóÔϻɢÄl¦éBåC³ð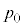 CCÌèðRCdÍÁ¬xÌ嫳ð
CCÌèðRCdÍÁ¬xÌ嫳ð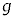 ƵAȺÌÝâɦæB
ƵAȺÌÝâɦæB
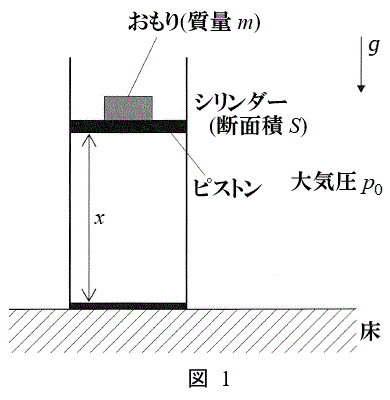 [A]@}1Ìæ¤ÉAfÊÏSÌV_[ª
½È°ÌãɼÉÅè³êÄ¢éBsXgÍV_[àÌCÌÆåCðdØé±ÆªÅ«AX±ÆȼûüÉç©É®BV_[êÊ©çsXg̺ÊÜÅÌ£ðp¢ÄAsXgÌÊuðxÆ\·BV_[AsXgÍfMÞÅÅ«Ä¢éB
[A]@}1Ìæ¤ÉAfÊÏSÌV_[ª
½È°ÌãɼÉÅè³êÄ¢éBsXgÍV_[àÌCÌÆåCðdØé±ÆªÅ«AX±ÆȼûüÉç©É®BV_[êÊ©çsXg̺ÊÜÅÌ£ðp¢ÄAsXgÌÊuðxÆ\·BV_[AsXgÍfMÞÅÅ«Ä¢éBÅA¿Êm̨àèðæ¹½sXgª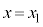 ÅÃ~µÄ¨èAsXg̺¤É·x
ÅÃ~µÄ¨èAsXg̺¤É·x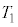 ÌP´qªqzC̪¶ßçêÄ¢½B
ÌP´qªqzC̪¶ßçêÄ¢½B
(a) V_[àÌCÌ̳ÍðßæB
ÉAsXgÉOÍðÁ¦AsXgÌÊuð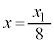 ÜÅäÁèÆÚ®³¹AV_[àÌCÌð³kµ½B
ÜÅäÁèÆÚ®³¹AV_[àÌCÌð³kµ½B
(b) sXgÌÊu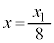 ɨ¯éV_[àÌCÌÌ·xðßæB
ɨ¯éV_[àÌCÌÌ·xðßæB
(c) ±Ì³kßöÅAV_[àÌC̪³ê½dðßæB
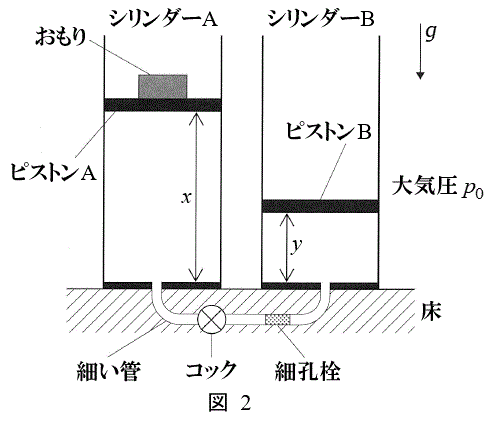 [B]@}2Ìæ¤ÉA¯¶fÊÏSðÂV_[ACV_[Bª
½È°ÌãɼÉÅè³êĨèARbNÆ×EðÌ¢½×¢ÇÅÂȪÁÄ¢éBsXgACsXgBÍA»ê¼êV_[AàAV_[BàÌCÌÆåCðdØé±ÆªÅ«AX±ÆȼûüÉç©É®BsXgAÉͨàèªæÁĨèAsXgBÉͨàèªæÁĢȢB×EðÍ×EÌ éÂßàÌÅ èA×Eððp¢é±ÆÅV_[AàAV_[BàÌCÌ̳Íð»ê¼êêèÉۿȪçCÌðÚ®³¹é±ÆªÅ«éBV_[AsXgARbNÆ×EðÌ¢½×¢ÇÍfMÞÅÅ«Ä¢éBV_[êÊ©çsXg̺ÊÜÅÌ£ðp¢ÄAsXgAÌÊuðxCsXgBÌÊuðyÆ\·B
[B]@}2Ìæ¤ÉA¯¶fÊÏSðÂV_[ACV_[Bª
½È°ÌãɼÉÅè³êĨèARbNÆ×EðÌ¢½×¢ÇÅÂȪÁÄ¢éBsXgACsXgBÍA»ê¼êV_[AàAV_[BàÌCÌÆåCðdØé±ÆªÅ«AX±ÆȼûüÉç©É®BsXgAÉͨàèªæÁĨèAsXgBÉͨàèªæÁĢȢB×EðÍ×EÌ éÂßàÌÅ èA×Eððp¢é±ÆÅV_[AàAV_[BàÌCÌ̳Íð»ê¼êêèÉۿȪçCÌðÚ®³¹é±ÆªÅ«éBV_[AsXgARbNÆ×EðÌ¢½×¢ÇÍfMÞÅÅ«Ä¢éBV_[êÊ©çsXg̺ÊÜÅÌ£ðp¢ÄAsXgAÌÊuðxCsXgBÌÊuðyÆ\·BÅARbNͶçêĨèAsXgAÍ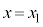 ÉAsXgBÍV_[Ìê(
ÉAsXgBÍV_[Ìê(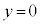 )ÉÃ~µÄ¢éBsXgA̺¤ÉÍ·x
)ÉÃ~µÄ¢éBsXgA̺¤ÉÍ·x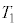 ÌP´qªqzC̪¶ßçêĨèACÌ̳ÍÍ
ÌP´qªqzC̪¶ßçêĨèACÌ̳ÍÍ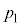 Å éB
Å éB
ÉARbNðJ«AsXgAÉ©©éÍÌÂè¢ðۿȪçAsXgAðäÁèƺûÉ®©µ½BRbNðJ¢½¼ãÌCÌÌóÔðóÔ1ÆæÔBsXgAðºûÉ®©µÄ¢ßöɨ¢ÄAV_[AàÌCÌÌêªA×EðÌ¢½×¢ÇðÊÁÄV_[BàɬüµAsXgBÍäÁèÆãûÉÚ®µ½B±ÌÆ«AV_[AàÌCÌÌ·xÍ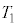 ÌÜÜÅ èAsXgBÉ©©éÍÍíÉÂèÁÄ¢½B
ÌÜÜÅ èAsXgBÉ©©éÍÍíÉÂèÁÄ¢½B
sXgAª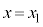 ©ç
©ç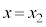 ÜÅÚ®µ½Æ«AsXgBÍ
ÜÅÚ®µ½Æ«AsXgBÍ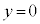 ©ç
©ç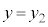 ÉÚ®µ½Æ·éB±ÌÆ«AV_[BàÌCÌÌ·xð
ÉÚ®µ½Æ·éB±ÌÆ«AV_[BàÌCÌÌ·xð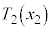 CCÌSÌÌàGlM[ð
CCÌSÌÌàGlM[ð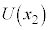 Æ»ê¼ê\·B
Æ»ê¼ê\·B
(d) sXgBÌÊu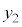 ðA
ðA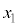 C
C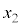 C
C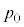 C
C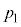 CSC
CSC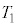 C
C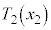 ̤¿KvÈàÌðp¢ÄßæB
̤¿KvÈàÌðp¢ÄßæB
(e) V_[AàÌC̪³ê½d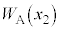 CV_[BàÌC̪µ½d
CV_[BàÌC̪µ½d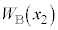 ðA
ðA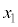 C
C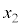 C
C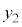 C
C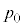 C
C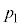 CS̤¿KvÈàÌðp¢ÄßæB
CS̤¿KvÈàÌðp¢ÄßæB
(f) V_[ACV_[Bɶßçê½CÌSÌÉεÄAMÍwæ1@¥ðl¦éBsXgAª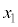 ©ç
©ç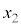 ÜÅÚ®µ½Æ«ÌàGlM[ÌÏ»ÍA
ÜÅÚ®µ½Æ«ÌàGlM[ÌÏ»ÍA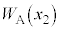 C
C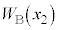 ðp¢ÄȺÌæ¤É¯éB
ðp¢ÄȺÌæ¤É¯éB 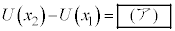 @(1)
@(1)±Ì±Æ©çAV_[BàÌCÌÌ·xÍ
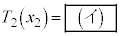 @(2)
@(2)ÆÜéBó C
C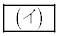 ÉÄÍÜé®ðßæB
ÉÄÍÜé®ðßæB ³çÉAsXgAðV_[AÌê(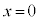 )ÜÅ®©µ½Æ«ACÌÍV_[BÌÝɶßçê½B±ÌCÌÌóÔðóÔ2ÆæÔB
)ÜÅ®©µ½Æ«ACÌÍV_[BÌÝɶßçê½B±ÌCÌÌóÔðóÔ2ÆæÔB
(g) óÔ1©çóÔ2Ìßöɨ¯éd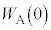 C
C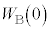 ÍA»ê¼êóÔ1àµÍóÔ2ɨ¯éCÌÌ·xA³ÍAÌÏÉæè\¹éB±Ì±Æðp¢éÆA·xTC³ÍpCÌÏVÌCÌÉÖµÄAàGlM[UÆ
ÍA»ê¼êóÔ1àµÍóÔ2ɨ¯éCÌÌ·xA³ÍAÌÏÉæè\¹éB±Ì±Æðp¢éÆA·xTC³ÍpCÌÏVÌCÌÉÖµÄAàGlM[UÆ ÌaÅ\³êéÊ
ÌaÅ\³êéÊ 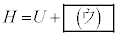 @(3)
@(3)ªA±ÌßöÌOãÅÏ»µÄ¢È¢±Æªí©éBTCpCV̤¿KvÈàÌðp¢Äó ð\¹B
ð\¹B
ܽA®(3)ÍP´qªqzCÌÌêACĮ̀¿Ênðp¢Ä 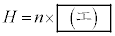 @(4)
@(4)ƯéATCVCR̤¿KvÈàÌðp¢Äó ð\¹B
ð\¹B
[C]@Ýâ[B]ÅÌÝèɨ¢ÄAzCÌÅÍÈAÀÝÌCÌ(ÀÝCÌ)ðp¢Ä¯lÌìðs¤BÀÝCÌÍAzCÌÆÍÙÈèAªqÔÉͽçÍƪq©gÌÌÏð³Å«È¢B»Ì½ßA®(4)É⳪ÁíèA
 @(5)
@(5)ªßöÌOãÅêèÉÛ½êéB±±ÅAaCbÍCÌÉæÁÄÜé³ÌÅ èAnÍÀÝCĮ̀¿ÊÅ éB
ÅARbNͶçêĨèAsXgAÍ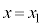 ÉAsXgBÍV_[Ìê(
ÉAsXgBÍV_[Ìê(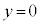 )ÉÃ~µÄ¢éBsXgA̺¤ÉÍ·x
)ÉÃ~µÄ¢éBsXgA̺¤ÉÍ·x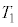 ÌÀÝC̪¶ßçêĨèA»ÌCÌ̳ÍÍ
ÌÀÝC̪¶ßçêĨèA»ÌCÌ̳ÍÍ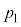 Å éB
Å éB
ÉARbNðJ«AsXgAÉ©©éÍÌÂè¢ðۿȪçAsXgAðäÁèƺûÉ®©µ½BRbNðJ¢½¼ãÌCÌÌóÔ(óÔ1)©çAV_[BÉÌÝɶßçê½CÌÌóÔ(óÔ2)ÖÌßöɨ¢ÄAV_[AàÌCÌÌ·xÍ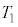 ÌÜÜÅ èAsXgBÉ©©éÍÍíÉÂèÁÄ¢½B
ÌÜÜÅ èAsXgBÉ©©éÍÍíÉÂèÁÄ¢½B
(h) ßöÌOãÅ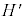 ªêèÉÛ½êé±Æðp·é±ÆÅAóÔ2ɨ¯éV_[BàÌÀÝCÌÌ·x
ªêèÉÛ½êé±Æðp·é±ÆÅAóÔ2ɨ¯éV_[BàÌÀÝCÌÌ·x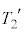 Í
Í 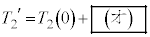 @(6)
@(6)Æ\³êéB±±ÅA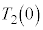 ÍzCÌðp¢½êÌóÔ2(
ÍzCÌðp¢½êÌóÔ2(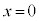 )ɨ¯éCÌÌ·xÅ éBóÔ1CóÔ2ɨ¯éCÌÌÌÏð»ê¼ê
)ɨ¯éCÌÌ·xÅ éBóÔ1CóÔ2ɨ¯éCÌÌÌÏð»ê¼ê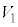 C
C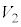 ƵAaCbCnCRC
ƵAaCbCnCRC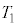 C
C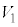 C
C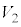 ̤¿KvÈàÌðp¢Äó
̤¿KvÈàÌðp¢Äó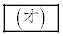 ð\¹B
ð\¹B
yLz±±©çLÅ·B²ÌF³Ü̲x²ððè½Aæ뵨袢½µÜ·B
yLzLͱ±ÜÅÅ·B
ð@IÕÍ©ÈèS^«ܷB(C)Å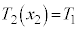 ÆÈÁĵܤÌÅA»à»à
ÆÈÁĵܤÌÅA»à»à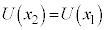 Å èA(g)ªÓ¡s¾ÉÈèÜ·ªA
Å èA(g)ªÓ¡s¾ÉÈèÜ·ªA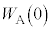 C
C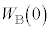 ÉÖ·éqg©ç(E)ðl¦Ü·B
ÉÖ·éqg©ç(E)ðl¦Ü·B
[A](a) sXgÉÍÍAåC³ªºü«ÉsXgð·Í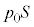 CV_[àÌCÌ̳Íð
CV_[àÌCÌ̳Íð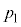 Ƶıêªãü«ÉsXgð·Í
Ƶıêªãü«ÉsXgð·Í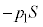 C¨àèÌdÍ
C¨àèÌdÍ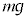 (ºü«)ÅA±êçÌÍÌÂè¢æèA
(ºü«)ÅA±êçÌÍÌÂè¢æèA 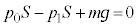 @
@ 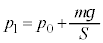 ......[]
......[]
(b) V_[àÌCÌÍfMÞÅÍÜêÄ¢éÌÅfMÏ»ðµÜ·BsXgÌÊu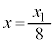 ɨ¯éV_[àÌCÌÌ·xð
ɨ¯éV_[àÌCÌÌ·xð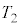 ƵÄA|Ab\ÌÖW®æèA
ƵÄA|Ab\ÌÖW®æèA 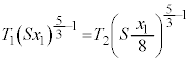 @
@ 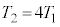 ......[]
......[]
sXgAª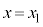 É¢éÆ«ÌV_[AàÌCÌÌÊð
É¢éÆ«ÌV_[AàÌCÌÌÊð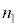 ƵÄAóÔûö®F
ƵÄAóÔûö®F 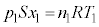 @¥¥¥@
@¥¥¥@
fMÏ»ÈÌÅA±Ì³kßöÅC̪zûµ½MÍ0CC̪³ê½dðWƵÄMÍwæ1@¥æèA 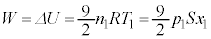 @(æ @)
@(æ @) 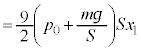 @(æ (a))
@(æ (a))
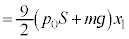 ......[]
......[]
[B]@sXgAª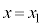 ©ç
©ç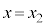 ÜÅÚ®·éÔAsXgAÉ©©éÍÌÂ袪۽êÄ¢éÌÅAV_[AàÌCÌ̳ÍÍ
ÜÅÚ®·éÔAsXgAÉ©©éÍÌÂ袪۽êÄ¢éÌÅAV_[AàÌCÌ̳ÍÍ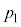 ÉÛ½êÜ·BsXgAª
ÉÛ½êÜ·BsXgAª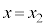 É¢éÆ«ÌV_[AàÌCÌÌÊð
É¢éÆ«ÌV_[AàÌCÌÌÊð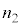 ƵÄAóÔûö®F
ƵÄAóÔûö®F 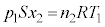 @¥¥¥A
@¥¥¥AA@æèA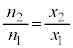 @
@ 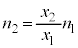 @¥¥¥B
@¥¥¥B
×¢ÇðÊÁÄV_[A©çV_[BÉÚ®µ½CÌÌÊÍA 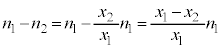 @¥¥¥C
@¥¥¥C
(d) sXgBÉ©©éÍÌÂè¢æèV_[BàÌCÌ̳ÍÍ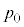 Å·BsXgBÌÊuª
Å·BsXgBÌÊuª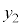 ÌÆ«ÌV_[BàÌCÌÌóÔûö®F
ÌÆ«ÌV_[BàÌCÌÌóÔûö®F 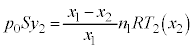 @¥¥¥D
@¥¥¥DD@æèA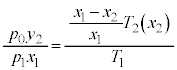
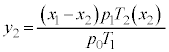 ......[]
......[]
(e) V_[AàÌCÌͳÍ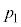 Ìè³Ï»ÅÌϪ
Ìè³Ï»ÅÌϪ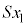 ¨
¨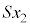 ÆÏ»·éÌÅAV_[AàÌC̪³ê½d
ÆÏ»·éÌÅAV_[AàÌC̪³ê½d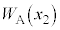 ÍA
ÍA 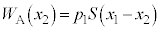 ......[]
......[]V_[BàÌCÌͳÍ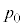 Ìè³Ï»ÅÌϪ0¨
Ìè³Ï»ÅÌϪ0¨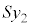 ÆÁ·éÌÅAV_[BàÌC̪µ½d
ÆÁ·éÌÅAV_[BàÌC̪µ½d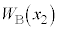 ÍA
ÍA 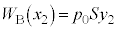 ......[]
......[]
(f) CÌSÌÉεÄMÍwæ1@¥ðl¦éÆACÌSÌÅzûµ½MÍ0ÅA
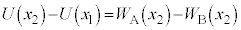 @(1)
@(1) 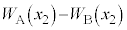 ......[A]
......[A]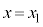 ÌÆ«V_[BàÉCÌÍÈAV_[AàÌCÌÌàGlM[ÍA
ÌÆ«V_[BàÉCÌÍÈAV_[AàÌCÌÌàGlM[ÍA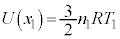
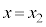 ÌÆ«V_[AàÌCÌÌÊÍBÌ
ÌÆ«V_[AàÌCÌÌÊÍBÌ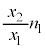 ÅAV_[BàÌCÌÌÊÍCÌ
ÅAV_[BàÌCÌÌÊÍCÌ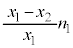 Å·B¼ÒÌàGlM[Ìa
Å·B¼ÒÌàGlM[Ìa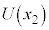 ÍA
ÍA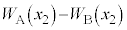 Í(e)ÌÊA(d)ÌÊðp¢ÄA
Í(e)ÌÊA(d)ÌÊðp¢ÄA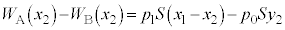 @¥¥¥E
@¥¥¥EæÁÄA(1)®ÍȺÌæ¤ÉÈèÜ·B
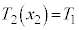 @
@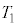 ......[C]
......[C]
(g) (e)ÌÊɨ¢Ä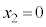 Æ·éÆA
Æ·éÆA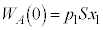 C
C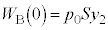
±êæèA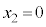 ÌÆ«(1)®ÍA
ÌÆ«(1)®ÍA ÆÈèÜ·ªA±êðA
ÆÝéÆA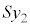 Í
Í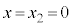 ÌÆ«(óÔ2)ÌCÌÌÌÏ
ÌÆ«(óÔ2)ÌCÌÌÌÏ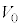 Å èA
Å èA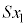 Í
Í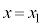 ÌÆ«(óÔ1)ÌCÌÌÌÏ
ÌÆ«(óÔ1)ÌCÌÌÌÏ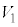 ÈÌÅA
ÈÌÅA ±êæèA·xTC³ÍpCÌÏVÌCÌÉÖµÄAàGlM[UÆ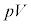 ÌaÅ\³êéÊ
ÌaÅ\³êéÊ 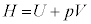 @(3)
@(3)ªAóÔ1¨óÔ2ÌßöÌOãÅÏ»µÄ¢È¢±Æªí©èÜ·B(1)®ÉEðüêÄÝéÆA
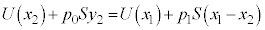 ÆÈèA
ÆÈèA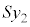 C
C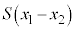 ðA
ðA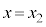 ÌÆ«ÌV_[BàAV_[AàÌCÌÌÌÏÆ©êÎAâÍè
ÌÆ«ÌV_[BàAV_[AàÌCÌÌÌÏÆ©êÎAâÍè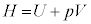 Í
Í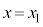 ÌÆ«Æ
ÌÆ«Æ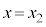 ÌÆ«ÆÅÏ»µÜ¹ñB@
ÌÆ«ÆÅÏ»µÜ¹ñB@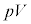 ......[E]P´qªqzCÌÅÍ
......[E]P´qªqzCÌÅÍ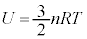 C
C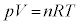 ÆÈéÌÅA
ÆÈéÌÅA 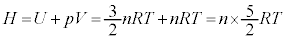 @
@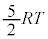 ......[G]
......[G]
[C]@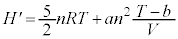 ªêèÉÛ½êéÌÅA
ªêèÉÛ½êéÌÅA 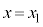 (óÔ1)ÌÆ«A
(óÔ1)ÌÆ«A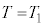 C
C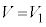
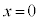 (óÔ2)ÌÆ«A
(óÔ2)ÌÆ«A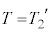 C
C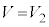
ƵÄA±±ÅA(C)ÌÊæè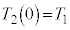 Å é±ÆAðÌ`ÉÓµÄA¶ÓÌ
Å é±ÆAðÌ`ÉÓµÄA¶ÓÌ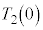 ÌWÆEÓÌ
ÌWÆEÓÌ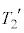 ÌWªµ¤æ¤ÉÏ`µA
ÌWªµ¤æ¤ÉÏ`µA ¼Óð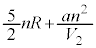 ÅèA
ÅèA 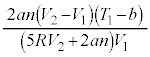 ......[I]
......[I]
yLz±±©çLÅ·B²ÌF³Ü̲x²ððè½Aæ뵨袢½µÜ·B
yLzLͱ±ÜÅÅ·B
@@Èwå¨TOP@@¨TOP@@TOPy[WÉßé
yLz±±©çLÅ·B²ÌF³Ü̲x²ððè½Aæ뵨袢½µÜ·B
yLzLͱ±ÜÅÅ·B
eâèÌì Í
oèåwÉ®µÜ·BȨAðÍA
êwywm§ìÅ·B©2005-2025(L)èéçé êwywm üïótInåwó±lbgmêwywm(²Äàͱ¿ç)²üïÍA
ܸA±¿çÜÅ[ð
¨è¾³¢B 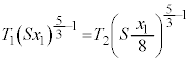 @
@ 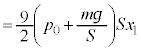 @(æ (a))
@(æ (a))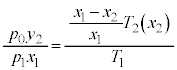
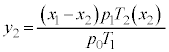 ......[]
......[]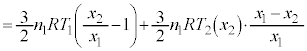
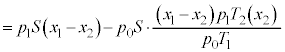
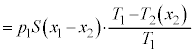
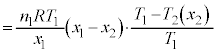 @(æ @)
@(æ @)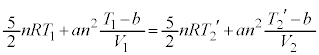
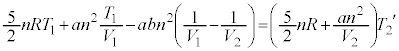
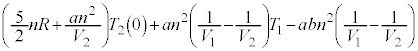
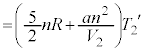
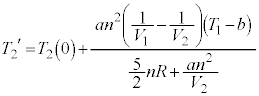
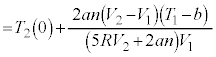
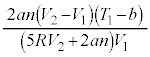 ......[I]
......[I]