���啨��'24�N�O��[2]
�ő̒��ɓd�ׂ��Œ肳�ꂽ���̂��G���N�g���b�g�ƌĂԁB�G���N�g���b�g�͐U���̃G�l���M�[��d�C�G�l���M�[�Ƃ��Ď��o���U�����d�Ȃǂ̕���ŗ��p����Ă���B�ȉ��ł́A�d�ׂ�тт��������U�d�̒��ɌŒ肳�ꂽ���̂��G���N�g���b�g�̃��f���Ƃ���B
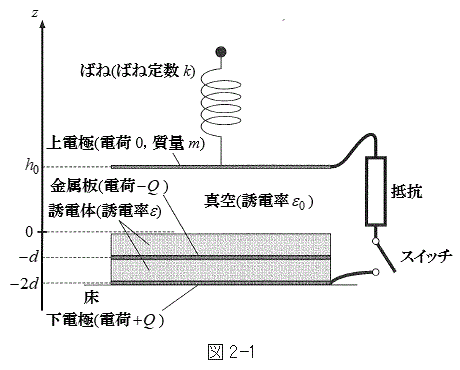 �}2-1�̂悤�ȑ��u���l����B�����ȏ��̏�ɕ��Ɖ��s����L�Ō����̖����ł��鐳���`�̋�����(���d��)���Œ肵���B���̏�ɕ��Ɖ��s����L�Ō�����
�}2-1�̂悤�ȑ��u���l����B�����ȏ��̏�ɕ��Ɖ��s����L�Ō����̖����ł��鐳���`�̋�����(���d��)���Œ肵���B���̏�ɕ��Ɖ��s����L�Ō�����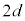 �̒����̂̌`��ŁA�����ɋ��������ߍ��܂ꂽ�U�d�̂��Œ肵���B���ߍ��܂ꂽ�����͕��Ɖ��s����L�Ō����������ł��A���̓d��
�̒����̂̌`��ŁA�����ɋ��������ߍ��܂ꂽ�U�d�̂��Œ肵���B���ߍ��܂ꂽ�����͕��Ɖ��s����L�Ō����������ł��A���̓d��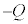 ��ттĂ���B�U�d�̗̂U�d����ε�ł���B��[���Œ肵���˒萔k�̐≏�̂̂˂�p���āA���Ɖ��s����L�Ō����̖����ł��鎿��m�̋�����(��d��)��U�d�̂̒���ɒ݂艺�����B���ׂĂ̋����ƗU�d�̂͏�����猩�ďd�Ȃ��Ă���B��d�ɂ͗U�d�̂ƕ��s��ۂ��Ȃ���㉺�����ɓ��������Ƃ��ł���B��d�ɂƉ��d�ɂ͒�R�ƃX�C�b�`����ē����łȂ���Ă���B���̑��u�͐^�ɒu����Ă���B�^��̗U�d����
��ттĂ���B�U�d�̗̂U�d����ε�ł���B��[���Œ肵���˒萔k�̐≏�̂̂˂�p���āA���Ɖ��s����L�Ō����̖����ł��鎿��m�̋�����(��d��)��U�d�̂̒���ɒ݂艺�����B���ׂĂ̋����ƗU�d�̂͏�����猩�ďd�Ȃ��Ă���B��d�ɂ͗U�d�̂ƕ��s��ۂ��Ȃ���㉺�����ɓ��������Ƃ��ł���B��d�ɂƉ��d�ɂ͒�R�ƃX�C�b�`����ē����łȂ���Ă���B���̑��u�͐^�ɒu����Ă���B�^��̗U�d����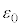 �ł���B�d�͉����x��
�ł���B�d�͉����x��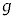 �Ƃ���B
�Ƃ���B
��d�ɂ̈ʒu��\�����߂ɁA�U�d�̂̏�ʂ���킸���ɏ�̈ʒu��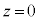 �ɂƂ�A�����������z�����Ƃ�B��d�ɂ̈ʒu��
�ɂƂ�A�����������z�����Ƃ�B��d�ɂ̈ʒu��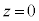 �̂Ƃ��A��d�ɂƗU�d�̏�ʂ̋����͖����ł���قǏ������B�d�ׂ́A��������ď�d�ɂƉ��d�ɂ̊Ԃł݈̂ړ�����B
�̂Ƃ��A��d�ɂƗU�d�̏�ʂ̋����͖����ł���قǏ������B�d�ׂ́A��������ď�d�ɂƉ��d�ɂ̊Ԃł݈̂ړ�����B
���������ŁA�}2-1�̂悤�ɃX�C�b�`�͊J���Ă���A���d�ɂ͓d��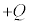 ��ттĂ����B��d�ɂ͓d�ׂ�ттĂ��炸�A�肠���̈ʒu
��ттĂ����B��d�ɂ͓d�ׂ�ттĂ��炸�A�肠���̈ʒu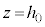 �ŐÎ~���Ă����B
�ŐÎ~���Ă����B
�����̋����ō��ꂽ�R���f���T�[���܂މ�H�ɂ��āA�ȉ��̐ݖ�ɓ�����B�������A�����̖ʐς͏\���ɑ傫���A�[�̌��ʂ͖����ł�����̂Ƃ���B��d�ɂɂȂ��ꂽ�����͏�d�ɂ̉^���ɂ͉e�����Ȃ��B�d�ׂ̈ړ�������̐U���ɔ����d���g�̔����͖����ł���B
�T�@�͂��߁A�}2-1�Ɏ������悤�ɉ��d�ɂ�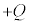 �̓d�ׂ�ттĂ���A�X�C�b�`�͊J���Ă���B��d�ɂ͂肠���̈ʒu
�̓d�ׂ�ттĂ���A�X�C�b�`�͊J���Ă���B��d�ɂ͂肠���̈ʒu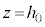 �ɂ���A�d�ׂ�ттĂ��Ȃ��B
�ɂ���A�d�ׂ�ттĂ��Ȃ��B
(1) �U�d�̂ɖ��ߍ��܂ꂽ�����̓d�ʂ����߂�B���d�ɂ�d�ʂ̊(�d��0)�Ƃ���B
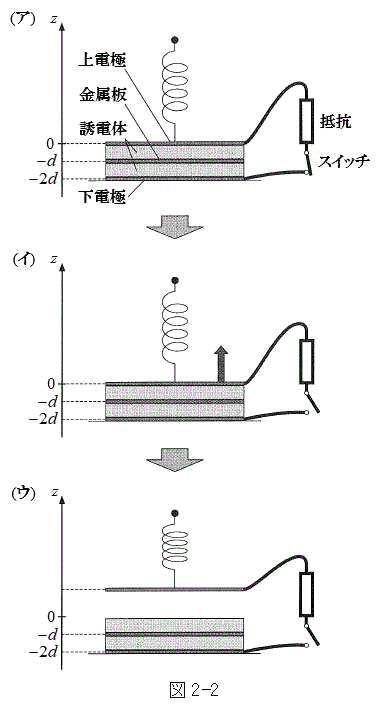 ���ɁA�}2-2(�A)�̂悤�ɁA��d�ɂ�
���ɁA�}2-2(�A)�̂悤�ɁA��d�ɂ�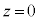 �̈ʒu�ɌŒ肵�A�X�C�b�`������B�\���������Ԃ��o�߂���ƁA��d�ɂ̓d�ׂ͈��ɂȂ����B
�̈ʒu�ɌŒ肵�A�X�C�b�`������B�\���������Ԃ��o�߂���ƁA��d�ɂ̓d�ׂ͈��ɂȂ����B
(2) ��d�ɂ̓d�ׂ����߂�B
�����Đ}2-2(�C)�̂悤�ɁA�X�C�b�`���J������A��d�ɂɊO�͂������A����ʒu�܂ł������ړ��������B���̈ʒu�ŏ�d�ɂ����R�ɓ����悤�ɂ����Ƃ���A�}2-2(�E)�̂悤�ɐÎ~�����܂܂ł������B
(3) ��d�ɂ�z���W�����߂�B
(4) ��d�ɂ̓d�ʂ����߂�B���d�ɂ�d�ʂ̊(�d��0)�Ƃ���B
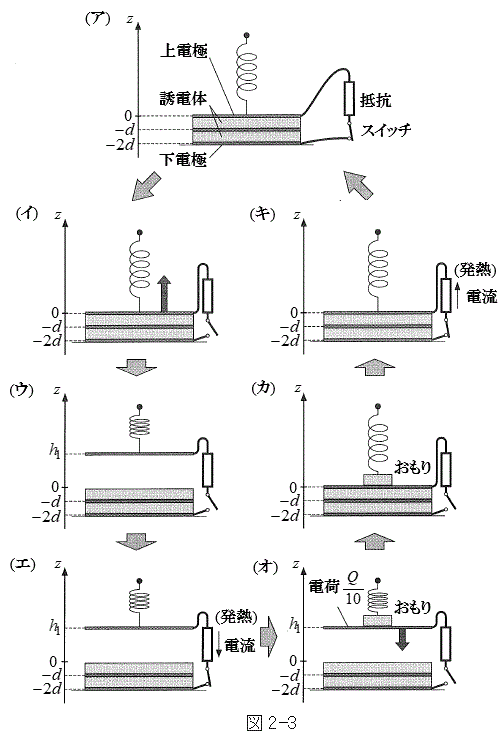 �U�@���ɁA�}2-3(�A)��(�C)��(�E)���E�E�E��(�L)��(�A)�Ŏ�����鏇�ɏ�d�ɂ����Ȃ���X�C�b�`���J�����Ƃ��̓d�ׂ̈ړ����R�̔��M�ׂ悤�B
�U�@���ɁA�}2-3(�A)��(�C)��(�E)���E�E�E��(�L)��(�A)�Ŏ�����鏇�ɏ�d�ɂ����Ȃ���X�C�b�`���J�����Ƃ��̓d�ׂ̈ړ����R�̔��M�ׂ悤�B�}2-3(�A)�̂悤�ɏ�d�ɂ�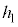 �Ɉړ����A�X�C�b�`������B�\���ɒ������Ԃ��o�߂��A��d�ɂ̓d�ׂ͈��ɂȂ����B���ɁA�}2-3(�C)�̂悤�ɃX�C�b�`���J���A��d�ɂ����R�ɓ����悤�ɂ����Ƃ���A������ɉ����x�^�����͂��߂��B��d�ɂ͐}2-3(�E)�̂悤��
�Ɉړ����A�X�C�b�`������B�\���ɒ������Ԃ��o�߂��A��d�ɂ̓d�ׂ͈��ɂȂ����B���ɁA�}2-3(�C)�̂悤�ɃX�C�b�`���J���A��d�ɂ����R�ɓ����悤�ɂ����Ƃ���A������ɉ����x�^�����͂��߂��B��d�ɂ͐}2-3(�E)�̂悤��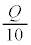 �܂ŏ㏸�����x��0�ɂȂ����B���̈ʒu�ŏ�d�ɂ�����ȏ㓮���Ȃ��悤�ɌŒ肵���B
�܂ŏ㏸�����x��0�ɂȂ����B���̈ʒu�ŏ�d�ɂ�����ȏ㓮���Ȃ��悤�ɌŒ肵���B
(1) 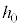 �����߂�B
�����߂�B �}2-3(�G)�̂悤�ɃX�C�b�`������Ƃ����R�ɓd�������ꔭ�M�����B�\���������Ԃ̂̂����M�͂�݁A��d�ɂ̓d�חʂ����̒l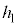 �ƂȂ����B
�ƂȂ����B
(2) �X�C�b�`����Ă���Ԃ̒�R�̔��M�ʂ̍��v���A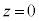 �Ck��p����
�Ck��p����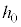 ���܂ގ��œ�����B
���܂ގ��œ�����B �}2-3(�I)�̂悤�ɏ�d�ɂɂ�������̂��ăX�C�b�`���J���A��d�ɂ����R�ɓ����悤�ɂ����Ƃ���A��d�ɂ͉��~���n�߁A�U�d�̂ɏՓ˂��邱�ƂȂ����x��0�ɂȂ����B�}2-3(�J)�̂悤�ɁA�Œ�_��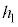 �ł������B���̈ʒu�ŏ�d�ɂ�����ȏ㓮���Ȃ��悤�ɌŒ肵���B
�ł������B���̈ʒu�ŏ�d�ɂ�����ȏ㓮���Ȃ��悤�ɌŒ肵���B
(3) ������̎��ʂ����߂�B
�}2-3(�L)�̂悤�ɂ��������菜���ăX�C�b�`������Ƃ����R�ɓd�������ꔭ�M�����B�\���ɒ������Ԃ̌�ɔ��M�͂�݁A�}2-3(�A)�Ɏ������͂��߂̏�Ԃɖ߂����B
(4) �}2-3�Ŏ������1�T�C�N���ɂ��āA��R�̔��M�ʂ̍��v���A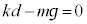 �Ck��p�����A
�Ck��p�����A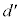 ���܂ގ��œ�����B
���܂ގ��œ�����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�d�ׂ��c��Ǘ������ߓ_�����R���f���T�[��H�ɂ˂ɂ��P�U�����g�ݍ��킳�ꂽ���ł��B���J�ɍl�@��i�߂�K�v������܂��B
�{��ł́A�˂̗͂��荇���̈ʒu����̕ψʂōl���܂��B�����ɒu���ꂽ�˂Ɏ���m�̂������݂艺����d�����˂����R������L�т��Ƃ��܂��B�͂̂荇�����A
�����ŁA����ɂ�����ɊO��f �������āA�˂������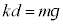 �L�т��Ƃ��܂��B�͂̂荇�����A
�L�т��Ƃ��܂��B�͂̂荇�����A
������A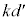 �Ȃ̂ŁA
�Ȃ̂ŁA
�܂�A�荇���̈ʒu����̂˂̐L�тɂ���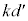 ��f ���荇���Ă���Ƃ��čl���܂��B
��f ���荇���Ă���Ƃ��čl���܂��B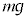 �Ȃ̂ŁA
�Ȃ̂ŁA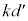 �̒��ɂ͏d��
�̒��ɂ͏d��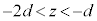 ���܂܂�Ă��܂��B�����ŁA�ȉ��ł́A�荇���̈ʒu����̕ψʂōl�����˂ɂ���
���܂܂�Ă��܂��B�����ŁA�ȉ��ł́A�荇���̈ʒu����̕ψʂōl�����˂ɂ���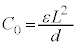 ���u�˂̒e���́{�d�́v�ƕ\�����܂��B
���u�˂̒e���́{�d�́v�ƕ\�����܂��B
�T(1) 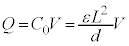 �̕������d���́A���d�ׂ������d�ɂ��畉�d�ׂ��������Ɍ��������ł��B���̕����ł��d����z�̑����ɔ����ĒႭ�Ȃ�܂��B���d�ɂƋ����̊Ԃɂł��Ă����R���f���T�[�̐Ód�e�ʂ�
�̕������d���́A���d�ׂ������d�ɂ��畉�d�ׂ��������Ɍ��������ł��B���̕����ł��d����z�̑����ɔ����ĒႭ�Ȃ�܂��B���d�ɂƋ����̊Ԃɂł��Ă����R���f���T�[�̐Ód�e�ʂ�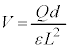 �ŁA�R���f���T�[�͓d��Q��~���Ă���A�����Ɖ��d�ɂ̊Ԃ̓d����V�Ƃ��āA
�ŁA�R���f���T�[�͓d��Q��~���Ă���A�����Ɖ��d�ɂ̊Ԃ̓d����V�Ƃ��āA 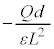 �@��
�@�� 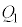
�����̓d�ʂ͉��d�ɂ���V�����Ⴍ�A���d�ɂ���Ƃ��������̓d�ʂ́A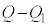 ......[��]
......[��]
(2) ��d�ɂ̓d�ׂ�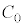 �Ƃ���ƁA���d�ɂ̓d�ׂ�
�Ƃ���ƁA���d�ɂ̓d�ׂ�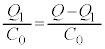 �ł��B��d�ɂƋ����̊Ԃɂł��Ă���R���f���T�[�̐Ód�e�ʂ�
�ł��B��d�ɂƋ����̊Ԃɂł��Ă���R���f���T�[�̐Ód�e�ʂ�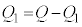 �ł��B�����Ə�d�ɂ̊Ԃ̓d���A�����Ɖ��d�ɂ̊Ԃ̓d���͓������̂ŁA
�ł��B�����Ə�d�ɂ̊Ԃ̓d���A�����Ɖ��d�ɂ̊Ԃ̓d���͓������̂ŁA ��d�ɂ̓d�ׂ͐��d�ׂŁA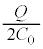 ......[��]
......[��] ���D��d�ɂƋ����̊Ԃɂł��Ă���R���f���T�[�ƁA���d�ɂƋ����̊Ԃɂł��Ă���R���f���T�[�́A���[�̓d�ʂ��������̂ŕ���������e����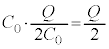 �ł��B�������ꂽ�R���f���T�[���[�̓d����
�ł��B�������ꂽ�R���f���T�[���[�̓d����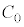 �C1�̃R���f���T�[���~����d�ׂ́A
�C1�̃R���f���T�[���~����d�ׂ́A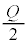 �ł��B
�ł��B
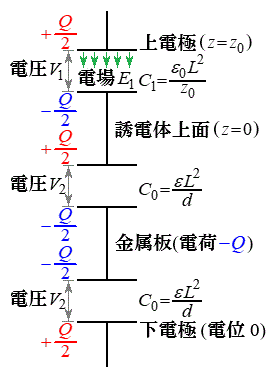 (3) �����Ə�d�ɂ̊Ԃ́A�U�d�̏�ʂɔ�������������Ƃ��āA�����ƗU�d�̏�ʂ̊Ԃ̗U�d�̂����镔���̃R���f���T�[(�Ód�e��
(3) �����Ə�d�ɂ̊Ԃ́A�U�d�̏�ʂɔ�������������Ƃ��āA�����ƗU�d�̏�ʂ̊Ԃ̗U�d�̂����镔���̃R���f���T�[(�Ód�e��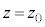 )�ƗU�d�̏�ʂƏ�d�ɂ̊Ԃ̐^�̕����̃R���f���T�[�ɕ����čl���܂��B�X�C�b�`���J������A��ɔɂ͓d��
)�ƗU�d�̏�ʂƏ�d�ɂ̊Ԃ̐^�̕����̃R���f���T�[�ɕ����čl���܂��B�X�C�b�`���J������A��ɔɂ͓d��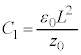 �����c����Ă��܂��B��d�ɂ�
�����c����Ă��܂��B��d�ɂ�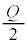 �̈ʒu�ŐÎ~���Ă���Ƃ��A��������U�d�̏�ʁA�����ď�d�ɂɌ����ēd�ʂ͍����Ȃ�A�d��̌����͉������ł��B�U�d�̏�ʂƏ�d�ɂ̊Ԃ̕����ɂł��Ă���R���f���T�[�̐Ód�e�ʂ�
�̈ʒu�ŐÎ~���Ă���Ƃ��A��������U�d�̏�ʁA�����ď�d�ɂɌ����ēd�ʂ͍����Ȃ�A�d��̌����͉������ł��B�U�d�̏�ʂƏ�d�ɂ̊Ԃ̕����ɂł��Ă���R���f���T�[�̐Ód�e�ʂ�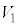 �ł��B�R���f���T�[���~����d�ׂ�
�ł��B�R���f���T�[���~����d�ׂ�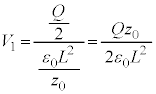 �ł��B�U�d�̏�ʂƏ�d�ɂ̊Ԃ̓d��
�ł��B�U�d�̏�ʂƏ�d�ɂ̊Ԃ̓d��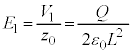 �́A
�́A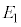 �@����@
�@����@�����ɂł��Ă���d��̋�����
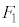 (�����͉�����)
(�����͉�����)�d��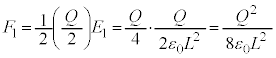 ����d�ɂɋy�ڂ��d�C���̑傫��
����d�ɂɋy�ڂ��d�C���̑傫��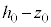 �́A
�́A 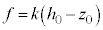 �@����A
�@����A�����͉������ł��B�˂��荇���̈ʒu����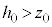 �L�тĂ���(�˂��k��ł���ꍇ�́A�d�C�͂��˂̗͂��������ŁA��d�ɂ͐Î~���܂���)�A�˂̒e���́{�d��f ��
�L�тĂ���(�˂��k��ł���ꍇ�́A�d�C�͂��˂̗͂��������ŁA��d�ɂ͐Î~���܂���)�A�˂̒e���́{�d��f ��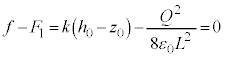 (
(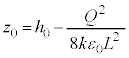 )�A�}2-2(�E)�ɂ������͂̂荇�����A
)�A�}2-2(�E)�ɂ������͂̂荇�����A �� 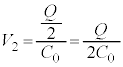 ......[��]�@����B
......[��]�@����B
(4) ���d�ɂƋ����̊Ԃ̓d��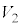 �́A
�́A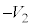 �C�����ƗU�d�̏�ʂ̊Ԃ̓d����
�C�����ƗU�d�̏�ʂ̊Ԃ̓d����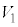 �ł��B���d�ɂ��������̕����d�ʂ͒Ⴍ�A���������U�d�̏�ʂ̕����d�ʂ͍����Ȃ�܂��B���d�ɂ̓d�ʂ�0�Ƃ���ƁA�����̓d�ʂ�
�ł��B���d�ɂ��������̕����d�ʂ͒Ⴍ�A���������U�d�̏�ʂ̕����d�ʂ͍����Ȃ�܂��B���d�ɂ̓d�ʂ�0�Ƃ���ƁA�����̓d�ʂ�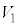 �C�U�d�̏�ʂ̓d�ʂ�0�C�U�d�̏�ʂƏ�d�ɂ̊Ԃ̓d���͇@��
�C�U�d�̏�ʂ̓d�ʂ�0�C�U�d�̏�ʂƏ�d�ɂ̊Ԃ̓d���͇@��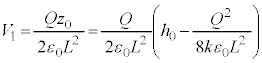 �ŁA��d�ɂ̓d�ʂ�
�ŁA��d�ɂ̓d�ʂ�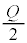 �ƂȂ�A
�ƂȂ�A 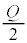 ......[��]
......[��]
�U�@�}2-3(�A)�̏́A�T�̐}2-2(�A)�̏Ɠ����ł��B�T(2)�Ɠ������A��d�ɂ̓d�ׂ�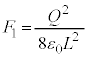 �C�}2-3(�C)�ŁA�X�C�b�`���J���ď�ɔ̓d��
�C�}2-3(�C)�ŁA�X�C�b�`���J���ď�ɔ̓d��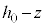 ���Ȃ��悤�ɂ��āA��d�ɂ����R�ɓ����悤�ɂ���ƁA��ɔƗU�d�̏�ʂƂ̊Ԃɂł���d�ꂪ��d�ɂɋy�ڂ��d�C�͇͂A���A�������ɑ傫��
���Ȃ��悤�ɂ��āA��d�ɂ����R�ɓ����悤�ɂ���ƁA��ɔƗU�d�̏�ʂƂ̊Ԃɂł���d�ꂪ��d�ɂɋy�ڂ��d�C�͇͂A���A�������ɑ傫��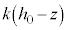 �ł�(�R���f���T�[�̋ɔԂ̓d�ꂪ�ɔ�̓d�ׂɋy�ڂ��͈͂��ł�)�B��ɔ�z���W��z�Ƃ��āA�˂̂荇���̈ʒu����̐L�т́A
�ł�(�R���f���T�[�̋ɔԂ̓d�ꂪ�ɔ�̓d�ׂɋy�ڂ��͈͂��ł�)�B��ɔ�z���W��z�Ƃ��āA�˂̂荇���̈ʒu����̐L�т́A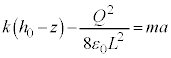 �ł��B�˂���ɔɋy�ڂ��e���́{�d�͂́A�������
�ł��B�˂���ɔɋy�ڂ��e���́{�d�͂́A�������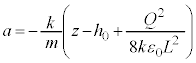 �ł��B��ɔ��^���������́A��ɔ̉����x��a�Ƃ��āA
�ł��B��ɔ��^���������́A��ɔ̉����x��a�Ƃ��āA 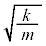 �@����C
�@����C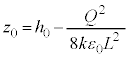
����āA��ɔ́A�p�U����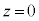 �C�U�����S
�C�U�����S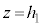 (�T(3)�ŋ��߂��e���́{�d�́{�d�C�͂̂荇���̈ʒu�ł�)���P�U�������܂��B
(�T(3)�ŋ��߂��e���́{�d�́{�d�C�͂̂荇���̈ʒu�ł�)���P�U�������܂��B
(1) �}2-3(�C)(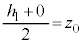 )�̏��P�U���̐U���[�ŁA��d�ɂ̑��x��0�ɂȂ����}2-3(�E)(
)�̏��P�U���̐U���[�ŁA��d�ɂ̑��x��0�ɂȂ����}2-3(�E)(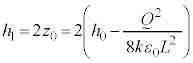 )�̏�������̐U���[�ł��B2�̐U���[�̒��_�͐U�����S�Ȃ̂ŁA
)�̏�������̐U���[�ł��B2�̐U���[�̒��_�͐U�����S�Ȃ̂ŁA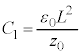 �ł���A�B���A
�ł���A�B���A 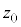 ......[��]
......[��]�}2-3(�C)���}2-3(�E)(�G)�̏��l���܂��B�}2-3(�E)(�G)�̏ŁA�U�d�̏�ʂƏ�d�ɂ̊Ԃɂł���R���f���T�[�̐Ód�e�ʂ́A�T(3)��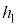 ��
��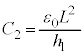 ��
��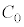 �Ƃ��āA
�Ƃ��āA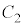 �ł��B�����Ə�d�ɂ̊Ԃ́A�Ód�e��
�ł��B�����Ə�d�ɂ̊Ԃ́A�Ód�e��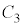 �̃R���f���T�[�ƐÓd�e��
�̃R���f���T�[�ƐÓd�e��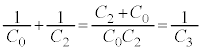 �̃R���f���T�[�̒���ڑ��ɂȂ��Ă���A�����e��
�̃R���f���T�[�̒���ڑ��ɂȂ��Ă���A�����e��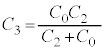 �́A
�́A ���A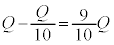 �ł��B
�ł��B
�X�C�b�`����ēd��������\�����Ԃ��o�߂�����A�}2-3(�G)�̏ŁA�����Ə�d�ɂ̊Ԃ̃R���f���T�[�̓d�ׂ�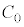 �ɂȂ�ƁA���d�ɂƋ����̊Ԃ̃R���f���T�[�̓d�ׂ́A
�ɂȂ�ƁA���d�ɂƋ����̊Ԃ̃R���f���T�[�̓d�ׂ́A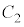 �ɂȂ�܂��B
�ɂȂ�܂��B
����������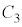 �C
�C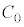 ����̃R���f���T�[
����̃R���f���T�[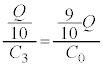 �ƁA�������牺�̃R���f���T�[
�ƁA�������牺�̃R���f���T�[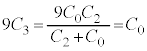 �͕���ڑ���ԂɂȂ��Ă��āA�d�����������̂ŁA
�͕���ڑ���ԂɂȂ��Ă��āA�d�����������̂ŁA
(2) ��蕶�Ɂu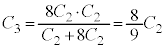 ���܂ގ��œ�����v�Ƃ���̂ŁA
���܂ގ��œ�����v�Ƃ���̂ŁA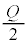 ���g���čl���܂��B
���g���čl���܂��B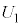 �ł��B
�ł��B �}2-3(�E)�̏ŁA���d�ɂƋ����̊Ԃ̃R���f���T�[���A�����Ə�d�ɂ̊Ԃ̃R���f���T�[���d��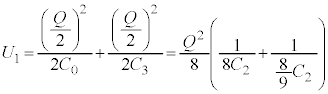 ��~���Ă���̂ŁA�R���f���T�[���~���Ă���S�Ód�G�l���M�[
��~���Ă���̂ŁA�R���f���T�[���~���Ă���S�Ód�G�l���M�[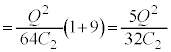 �́A
�́A �X�C�b�`����ēd��������\�����Ԃ��o�߂�����̑S�Ód�G�l���M�[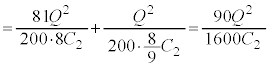 �́A
�́A ��R�̔��M�ʂ́A�R���f���T�[���������Ód�G�l���M�[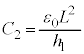 �ɓ������A
�ɓ������A 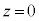 ���A
���A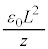 ......[��]
......[��]
(3) ��d�ɂ�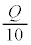 �ɗ��Ă��A��d�ɂƗU�d�̏�ʂ̊Ԃɖ����ł���قǏ������Ă��A�������c���Ă���Ƃ�����蕶�̎w��ɒ��ӂ��܂��B�܂�A���̂Ƃ��ɂ��U�d�̏�ʂƏ�d�ɂ̊Ԃ̃R���f���T�[�͎c���Ă��܂��B��d�ɂ�z���W��z�̂Ƃ��A��d�ɂƗU�d�̏�ʂ̊Ԃɂł��Ă���R���f���T�[�̐Ód�e�ʂ�
�ɗ��Ă��A��d�ɂƗU�d�̏�ʂ̊Ԃɖ����ł���قǏ������Ă��A�������c���Ă���Ƃ�����蕶�̎w��ɒ��ӂ��܂��B�܂�A���̂Ƃ��ɂ��U�d�̏�ʂƏ�d�ɂ̊Ԃ̃R���f���T�[�͎c���Ă��܂��B��d�ɂ�z���W��z�̂Ƃ��A��d�ɂƗU�d�̏�ʂ̊Ԃɂł��Ă���R���f���T�[�̐Ód�e�ʂ�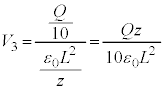 �ł��B�R���f���T�[�͓d��
�ł��B�R���f���T�[�͓d��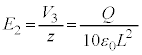 �������Ă���̂ŁA���̃R���f���T�[�̋ɔԓd���́A
�������Ă���̂ŁA���̃R���f���T�[�̋ɔԓd���́A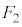 �C�ɔԂ̓d��̋����́A
�C�ɔԂ̓d��̋����́A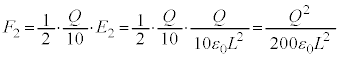 (�����͉�����)�C���̂Ƃ��d�ꂪ��ɔɋy�ڂ��d�C��
(�����͉�����)�C���̂Ƃ��d�ꂪ��ɔɋy�ڂ��d�C��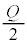 �̑傫���́A
�̑傫���́A 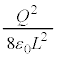 �@(������)
�@(������)���D���̓d�C�͂́A�U�d�̏�ʂƏ�d�ɂ̋����������ł���قǏ������Ă����ł��邱�Ƃɒ��ӂ��܂��B
��d�ɂ̓d�ׂ�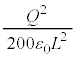 �̂Ƃ��̉^���������C�Ɣ�ׂāA��d�ɂ�z���W��z�̂Ƃ��̂˂̒e���́{�d�͕͂ς�炸�A�d�C�͂�
�̂Ƃ��̉^���������C�Ɣ�ׂāA��d�ɂ�z���W��z�̂Ƃ��̂˂̒e���́{�d�͕͂ς�炸�A�d�C�͂�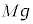 ��
��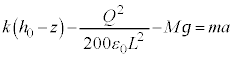 �ƂȂ�A������̎��ʂ�M�Ƃ��Ă�����ɓ����d��
�ƂȂ�A������̎��ʂ�M�Ƃ��Ă�����ɓ����d��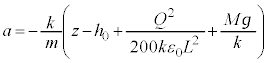 �������A��d�ɂ̉^���������́A
�������A��d�ɂ̉^���������́A �ƂȂ�A��͂�P�U���ł����A��蕶�́u�Œ�_��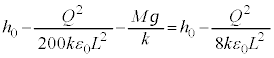 �ł������v�Ƃ����L�q����A���̒P�U���́A�C�Ɠ������A
�ł������v�Ƃ����L�q����A���̒P�U���́A�C�Ɠ������A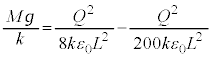 ��U�����S�Ƃ���P�U���łȂ���Ȃ�܂���B����āA
��U�����S�Ƃ���P�U���łȂ���Ȃ�܂���B����āA 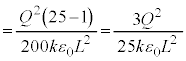 �@����D
�@����D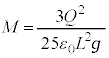
�� 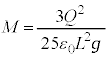 ......[��]
......[��] ���D��L�ł́A�^���������𗧂ĂāA�P�U�����l�@���܂������A��Ԃ�������܂��B�P�U���̐U�����S�́A�荇���̈ʒu�ł���A�U�����S�������A�Ƃ������Ƃ́A�荇���̈ʒu�������A�Ƃ������Ƃł���A���Ăɂ́A�u�荇���̈ʒu�͕ς��Ȃ�����v�Ƃ��ćD���𗧂Ă�̂�OK�ł��B
(4) �}2-3�Ŏ������1�T�C�N���ŁA���u����d���́A������ɓ����d�͂�����d���A�����A��������ʒu�G�l���M�[�ł��B��R�Ŕ������锭�M�ʂ́A������̈ʒu�G�l���M�[�̌������ł���Ƃ��āA(3)�̌��ʂ�p���āA 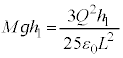 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 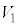 �ł��B�R���f���T�[���~����d�ׂ�
�ł��B�R���f���T�[���~����d�ׂ�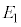 �@����@
�@����@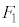 (�����͉�����)
(�����͉�����)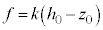 �@����A
�@����A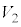
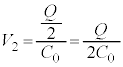 ......[��]�@����B
......[��]�@����B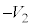 �C�����ƗU�d�̏�ʂ̊Ԃ̓d����
�C�����ƗU�d�̏�ʂ̊Ԃ̓d����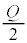 ......[��]
......[��]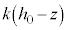 �ł�(�R���f���T�[�̋ɔԂ̓d�ꂪ�ɔ�̓d�ׂɋy�ڂ��͈͂��ł�)�B��ɔ�z���W��z�Ƃ��āA�˂̂荇���̈ʒu����̐L�т́A
�ł�(�R���f���T�[�̋ɔԂ̓d�ꂪ�ɔ�̓d�ׂɋy�ڂ��͈͂��ł�)�B��ɔ�z���W��z�Ƃ��āA�˂̂荇���̈ʒu����̐L�т́A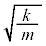 �@����C
�@����C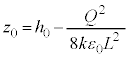
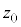 ......[��]
......[��]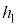 ��
��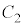 �ł��B�����Ə�d�ɂ̊Ԃ́A�Ód�e��
�ł��B�����Ə�d�ɂ̊Ԃ́A�Ód�e��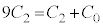 �@��
�@�� 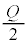 ���g���čl���܂��B
���g���čl���܂��B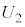
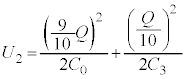
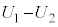
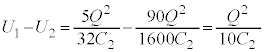
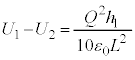
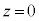 ���A
���A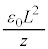 ......[��]
......[��]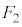 �C�ɔԂ̓d��̋����́A
�C�ɔԂ̓d��̋����́A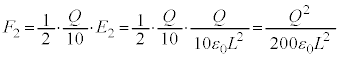 (�����͉�����)�C���̂Ƃ��d�ꂪ��ɔɋy�ڂ��d�C��
(�����͉�����)�C���̂Ƃ��d�ꂪ��ɔɋy�ڂ��d�C��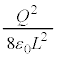 �@(������)
�@(������)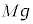 ��
��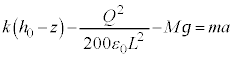 �ƂȂ�A������̎��ʂ�M�Ƃ��Ă�����ɓ����d��
�ƂȂ�A������̎��ʂ�M�Ƃ��Ă�����ɓ����d��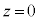
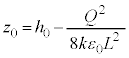
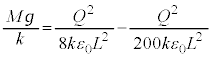 ��U�����S�Ƃ���P�U���łȂ���Ȃ�܂���B����āA
��U�����S�Ƃ���P�U���łȂ���Ȃ�܂���B����āA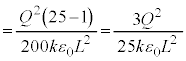 �@����D
�@����D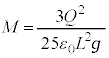
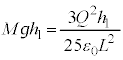
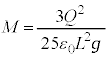 ......[��]
......[��]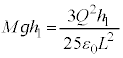 ......[��]
......[��]