�g���E���g���K���(����2)
���l�s�啨��'07�N[3]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���s�Ȑ��H����A�����A�Ɖ�����B���Î~�A�܂��͋t�����Ɉ��̑����ňړ����Ă���B���B�̐擪�ɂ���x�J���炷�x�J�����A���A�ɏ���Ă���ϑ��҂������Ă���ꍇ�ɂ��Ĉȉ��̖₢(1)�`(3)�ɓ�����B�������A���B�̔�����x�J���̐U������ �C������c�Ƃ���B���A�̐i�s�����Ɨ��A���猩�����B�̕����Ƃ̂Ȃ��p��θ�Ƃ���B�܂��A�����͗�Ԃ̑��������\���傫���A�㉺���̐��H�Ԃ̋����͌x�J���̔g�������\�������Ƃ���B
�C������c�Ƃ���B���A�̐i�s�����Ɨ��A���猩�����B�̕����Ƃ̂Ȃ��p��θ�Ƃ���B�܂��A�����͗�Ԃ̑��������\���傫���A�㉺���̐��H�Ԃ̋����͌x�J���̔g�������\�������Ƃ���B
 (1) �}1�̂悤�ɗ��A���_
(1) �}1�̂悤�ɗ��A���_ �ŐÎ~���A���B������
�ŐÎ~���A���B������ �ő����Ă���ꍇ���l����B
�ő����Ă���ꍇ���l����B(a) ��Ԃ��_Y��ʉ߂����Ƃ��ɂ���g�ʂ��o����A�_ ��ʉ߂����Ƃ��Ɏ��̔g�ʂ��o���ꂽ�Ƃ���B���̂Ƃ��̋���
��ʉ߂����Ƃ��Ɏ��̔g�ʂ��o���ꂽ�Ƃ���B���̂Ƃ��̋��� �����߂�B
�����߂�B (b)  �Ƃ���B�_Y��蔭����ꂽ���g���_
�Ƃ���B�_Y��蔭����ꂽ���g���_ �ɓ��B���Ă���A�_
�ɓ��B���Ă���A�_ ��蔭����ꂽ���g���_
��蔭����ꂽ���g���_ �ɓ��B����܂ł̎��Ԃ����߂�B
�ɓ��B����܂ł̎��Ԃ����߂�B  (2) �}2�ɂ悤�ɁA���A������
(2) �}2�ɂ悤�ɁA���A������ �ő����Ă��āA���B���Î~���Ă���ꍇ�ɂ��čl����B
�ő����Ă��āA���B���Î~���Ă���ꍇ�ɂ��čl����B(a) ���A�̑��x�� �������������߂�B
�������������߂�B (b) ����Z�����ԂɁA���A�̊ϑ��҂�����g�ʂ̐����v�Z���邱�Ƃɂ��A�ϑ��҂������x�J���̐U���� �����߂�B�������A�Z�����Ԃł́A(a)�ŋ��߂������͕ω����Ȃ��Ƃ��Ă悢�B
�����߂�B�������A�Z�����Ԃł́A(a)�ŋ��߂������͕ω����Ȃ��Ƃ��Ă悢�B  (3) �}3�̂悤�ɁA���A�Ɨ��B����������
(3) �}3�̂悤�ɁA���A�Ɨ��B���������� �ő����Ă���ꍇ���l����B
�ő����Ă���ꍇ���l����B(a) ���A�̊ϑ��҂������x�J���̐U���� ��c�C
��c�C �Cθ�C
�Cθ�C ��p���ĕ\���B
��p���ĕ\���B [��]
����啨��'08�N[3]
���̕��͂��@�@�ɓK���Ȍ��܂��͐���������B
�d�Ԃ̋O�������������ɁA���H����k�����ɂ��ꂼ�꒼���I�ɔz�u����A�������Ă���B�O���Ɠ��H���������铥�����_O�Ƃ��A����������x���A��k������y�����Ƃ�B�d�Ԃ͐U���� �̌x�J��炵�Ȃ���A�����瓌�̕����ֈ��̑��x
�̌x�J��炵�Ȃ���A�����瓌�̕����ֈ��̑��x �ő��s���Ă���B���܁A�d�Ԃ����_���瓌��
�ő��s���Ă���B���܁A�d�Ԃ����_���瓌�� (
( )�̈ʒuQ�ɂ����������Ă���B�������A������
)�̈ʒuQ�ɂ����������Ă���B�������A������ �Ƃ���B
�Ƃ���B
�d�Ԃ��ʒuQ��ʉ߂���Ƃ��A���̈ʒu�ɂ���ϑ���A�ɕ�������x�J���̐U�������@���@ �ł���A
�ł���A �Ƃ͈قȂ��Ă���B���̌��ۂ��@���@�Ƃ����B
�Ƃ͈قȂ��Ă���B���̌��ۂ��@���@�Ƃ����B
�d�Ԃ��ʒuQ��ʉ߂������ƂɁA�������� �̈ʒuP�ɂ���ϑ���B�ɕ�������x�J���̐U�����͎��̎菇�ŋ��߂���B
�̈ʒuP�ɂ���ϑ���B�ɕ�������x�J���̐U�����͎��̎菇�ŋ��߂���B
�ʒuQ�Ŕ������x�J�����ʒuP�ɓ��B����̂ɗv���鎞�Ԃ��@���@ �ł���A���̊Ԃɓd�Ԃ͈ʒu
�ł���A���̊Ԃɓd�Ԃ͈ʒu �܂Ői�݁A���̈ړ�����
�܂Ői�݁A���̈ړ����� ���@���@
���@���@ �ł���B�܂��A���̊Ԃɔ������x�J���̔g�̌����@���@�ł���B�ʒuP�ɂ���ϑ���B�ɕ�������x�J����
�ł���B�܂��A���̊Ԃɔ������x�J���̔g�̌����@���@�ł���B�ʒuP�ɂ���ϑ���B�ɕ�������x�J���� �Ԃ��@���@�̔g�����������ł���A���̔g�����@���@
�Ԃ��@���@�̔g�����������ł���A���̔g�����@���@ �ƂȂ�B���������āA�ϑ���B�ɕ�������x�J���̐U�������@���@
�ƂȂ�B���������āA�ϑ���B�ɕ�������x�J���̐U�������@���@ �ƂȂ�B
�ƂȂ�B
[��]
�k�啨��'10�N���[3]
���̕��͂� (1) ���� (8) �ɓK�Ȑ���������B�܂��A (a) �C (b) �ɂ́Am�C �C
�C �C
�C �̒�����I��ŋL������B
�̒�����I��ŋL������B
 ��1�@�}1�̂悤�ȑ��u�̓N�C���P�ǂƌĂ�AA������������͍��ƉE�ɕ�����Đi�݁A�Ăяo����Ċ���B�ŕ�������B�E���̊ǂ͉��ŁA���̒�����A���I�ɕω������邱�Ƃ��ł���B
��1�@�}1�̂悤�ȑ��u�̓N�C���P�ǂƌĂ�AA������������͍��ƉE�ɕ�����Đi�݁A�Ăяo����Ċ���B�ŕ�������B�E���̊ǂ͉��ŁA���̒�����A���I�ɕω������邱�Ƃ��ł���B
B�ł̉��̋����́A���̔g���� �C���ƉE�̌o�H�̍���
�C���ƉE�̌o�H�̍��� �Ƃ����Ƃ��A����m��p���āA
�Ƃ����Ƃ��A����m��p���āA (a) �̂Ƃ����߂����đ傫���Ȃ�A
(a) �̂Ƃ����߂����đ傫���Ȃ�A (b) �̂Ƃ��ł����������ď������Ȃ�B���̎��g����
(b) �̂Ƃ��ł����������ď������Ȃ�B���̎��g���� �̂Ƃ��ɁA�}1�̂悤�ɉE�̊ǂ��������ƈ����o���Ƌ���
�̂Ƃ��ɁA�}1�̂悤�ɉE�̊ǂ��������ƈ����o���Ƌ��� ���Ƃ�B�ŕ������鉹�̋������������Ȃ����B���̂Ƃ��̔g����X��p���� (1)
���Ƃ�B�ŕ������鉹�̋������������Ȃ����B���̂Ƃ��̔g����X��p���� (1)  �ƕ\����A���̑�����
�ƕ\����A���̑����� (2)
(2)  �ł��邱�Ƃ��킩��B���ɁA�E�̊ǂ��Œ肵�ĉ��̎��g�����������ƕω��������Ƃ���A���g����
�ł��邱�Ƃ��킩��B���ɁA�E�̊ǂ��Œ肵�ĉ��̎��g�����������ƕω��������Ƃ���A���g���� �ω����邲�Ƃ�B�ŕ������鉹�̋������������Ȃ����B���̑���v�͎��g���ɂ��Ȃ��Ƃ���ƁA���̂Ƃ��̍��ƉE�̊ǂ̌o�H�̍���f ��v��p���� (3)
�ω����邲�Ƃ�B�ŕ������鉹�̋������������Ȃ����B���̑���v�͎��g���ɂ��Ȃ��Ƃ���ƁA���̂Ƃ��̍��ƉE�̊ǂ̌o�H�̍���f ��v��p���� (3)  �ƕ\�����B
�ƕ\�����B
 ��2�@���l�̌��ۂ́A����p���Ă��m���߂���B�}2�ŁAP�͐^�ł̔g����
��2�@���l�̌��ۂ́A����p���Ă��m���߂���B�}2�ŁAP�͐^�ł̔g���� �̒P�F�������o��������AH�͌��̈ꕔ�߂��ꕔ�˂��锼�������A
�̒P�F�������o��������AH�͌��̈ꕔ�߂��ꕔ�˂��锼�������A ��
�� �͌����ɐ����ɒu���ꂽ���ʋ��ł���B����P����̌�����H��2�̕����ɕ�����ꂽ��A���ꂼ��
�͌����ɐ����ɒu���ꂽ���ʋ��ł���B����P����̌�����H��2�̕����ɕ�����ꂽ��A���ꂼ�� ��
�� �Ŕ��˂���A�Ă�H���o��Q�ւƓ����ꊱ����B���u�S�̂͐^�ɒu����AH��
�Ŕ��˂���A�Ă�H���o��Q�ւƓ����ꊱ����B���u�S�̂͐^�ɒu����AH�� �̊Ԃɂ́A�����̕�
�̊Ԃɂ́A�����̕� �̓����e��C���u����Ă���B
�̓����e��C���u����Ă���B
�ŏ��AQ�ɂ����Č����ł����������ĈÂ���Ԃ��� ���������ƉE������
���������ƉE������ �������s�ړ��������Ƃ���AQ�ł̌��́C���Â̎�����100��J��Ԃ��Â���ԂƂȂ����B���̂Ƃ���
�������s�ړ��������Ƃ���AQ�ł̌��́C���Â̎�����100��J��Ԃ��Â���ԂƂȂ����B���̂Ƃ��� �̈ړ�����x��
�̈ړ�����x�� ��p���� (4)
��p���� (4)  �ƕ\�����B���ɁA�e��C������C�̂ł������Ɩ��������Ƃ���A�e������̋��ܗ���1����n�ւƘA���I�ɑ������AQ�ł̌��͈Â���Ԃ���k��̖��Â̎������J��Ԃ��A�Â���ԂƂȂ����B�^�̌��̑�����
�ƕ\�����B���ɁA�e��C������C�̂ł������Ɩ��������Ƃ���A�e������̋��ܗ���1����n�ւƘA���I�ɑ������AQ�ł̌��͈Â���Ԃ���k��̖��Â̎������J��Ԃ��A�Â���ԂƂȂ����B�^�̌��̑����� �Ƃ���ƁA���ܗ�n�̗e�풆������d�����i�ނ̂ɕK�v�Ȏ��Ԃ� (5)
�Ƃ���ƁA���ܗ�n�̗e�풆������d�����i�ނ̂ɕK�v�Ȏ��Ԃ� (5)  �Ȃ̂ŁA�������ԓ��ɐ^�Ō��̐i�ނ��Ƃ̂ł��鋗���� (6)
�Ȃ̂ŁA�������ԓ��ɐ^�Ō��̐i�ނ��Ƃ̂ł��鋗���� (6)  �ł���B���̂��Ƃ���A�e����C�̂Ŗ����������Ƃ́A�^�ł̌o�H���������� (7)
�ł���B���̂��Ƃ���A�e����C�̂Ŗ����������Ƃ́A�^�ł̌o�H���������� (7)  �����L�т����ƂƓ����ł��邱�Ƃ��킩��B���������āA�C�̂̋��ܗ�n��k��p���� (8) �Ƌ��߂邱�Ƃ��ł���B
�����L�т����ƂƓ����ł��邱�Ƃ��킩��B���������āA�C�̂̋��ܗ�n��k��p���� (8) �Ƌ��߂邱�Ƃ��ł���B
[��]
���k�啨��'10�N�O��[3]
 �}1�Ɏ����悤�Ȓ���
�}1�Ɏ����悤�Ȓ��� �ŗ��[�̊J������(�J��)���Az����̉�]���ɊJ�ǂ̒��S�����_�ƈ�v����悤�ɌŒ肳��Ă���B��]�������̕����ɉ�邱�Ƃɂ��A�J�ǂ�x-y���ʓ���z���̐��������猩�Ĕ����v���ɉ�]�ł���B�J�Ǔ����ɂ͒���g���M��ɐڑ����ꂽ���^�X�s�[�J�[�����t�����Ă���B����g���M�킩��K�ȐU�����̐����g�����^�X�s�[�J�[�ɓ��͂���ƁA�J�Ǔ��̋C���ɗ����̊J���[�����̈ʒu�ƂȂ���g����邱�Ƃ��ł���B���g�������Ƃ������́A�����̊J���[���o���ƂȂ���͂ɓ`���B���̉��̔g�`�́Ax-y���ʏ�ɒu���ꂽ�}�C�N��ʂ��ăI�V���X�R�[�v�Œ��ׂ邱�Ƃ��ł���B
�ŗ��[�̊J������(�J��)���Az����̉�]���ɊJ�ǂ̒��S�����_�ƈ�v����悤�ɌŒ肳��Ă���B��]�������̕����ɉ�邱�Ƃɂ��A�J�ǂ�x-y���ʓ���z���̐��������猩�Ĕ����v���ɉ�]�ł���B�J�Ǔ����ɂ͒���g���M��ɐڑ����ꂽ���^�X�s�[�J�[�����t�����Ă���B����g���M�킩��K�ȐU�����̐����g�����^�X�s�[�J�[�ɓ��͂���ƁA�J�Ǔ��̋C���ɗ����̊J���[�����̈ʒu�ƂȂ���g����邱�Ƃ��ł���B���g�������Ƃ������́A�����̊J���[���o���ƂȂ���͂ɓ`���B���̉��̔g�`�́Ax-y���ʏ�ɒu���ꂽ�}�C�N��ʂ��ăI�V���X�R�[�v�Œ��ׂ邱�Ƃ��ł���B
����ǂȂǂ́A�����ʉ߂���є��˂����Ȃ��ގ��łł��Ă���Ƃ��āA�ȉ��̖₢�ɓ�����B�́A�p���̏���̏ꏊ�ɋL������B�܂��A���ʂ����łȂ��l������v�Z�̉ߒ����L���B
��(1) �}1�̂悤�ɁA�J�ǂ̒��S����y���ƈ�v�����ĊJ�ǂ�Î~�������B����g���M��̐U�������[������������Ƒ��������Ă����ƁA����U�����ɂȂ����Ƃ��J�Ǔ��̋C���Ɋ�{�U���̒��g���ł��A�J���[���特�������n�߂��B���̉���x����ɒu���ꂽ�}�C�N��ʂ��ăI�V���X�R�[�v�Œ��ׂ��B�I�V���X�R�[�v�̎��Ԏ�1�ڐ���̊Ԋu�� (
( �~���b)�ɂ����Ƃ���A�}2�Ŏ����悤�Ȕg�`���ϑ����邱�Ƃ��ł����B
�~���b)�ɂ����Ƃ���A�}2�Ŏ����悤�Ȕg�`���ϑ����邱�Ƃ��ł����B (a) �I�V���X�R�[�v�ɕ\�����ꂽ�g�`����A���g�̎��� �̐��l����ѐU����
�̐��l����ѐU���� �̐��l�����߂�B
�̐��l�����߂�B (b) ������ �ł���Ƃ��A�}2�Ŋϑ��������̔g��
�ł���Ƃ��A�}2�Ŋϑ��������̔g�� �̐��l���A�L������2���ŋ��߂�B
�̐��l���A�L������2���ŋ��߂�B (c) �J�Ǔ��̋C���̌ŗL�U���̂����A�g���� �ɑΉ��������g���M��̐U����
�ɑΉ��������g���M��̐U���� �̐��l�����߂�B
�̐��l�����߂�B  (d) ����g���M��̐U������f �ɌŒ肵�āA�J�Ǔ��̋C���ɍ������g�̔g����
(d) ����g���M��̐U������f �ɌŒ肵�āA�J�Ǔ��̋C���ɍ������g�̔g���� �Ƃ����B2�̊J���[����o�����̊��ׂ邽�߁A�}�C�N��
�Ƃ����B2�̊J���[����o�����̊��ׂ邽�߁A�}�C�N�� �̐����y���������Ɉړ��������B�}�C�N��ʂ��ăI�V���X�R�[�v�ő��肵���U���ƃ}�C�N��y���W�ʒu�̊W�������ł��K�ȃO���t���A�}3��(�A)�`(�J)�̒�����1�I�ׁB�܂��A���̃O���t��I���R���L���B�Ȃ��A�O���t�����₷�����邽�߂ɁA���Ŏ�������l�͂Ȃ߂炩�Ȕj���Ō���ł���B
�̐����y���������Ɉړ��������B�}�C�N��ʂ��ăI�V���X�R�[�v�ő��肵���U���ƃ}�C�N��y���W�ʒu�̊W�������ł��K�ȃO���t���A�}3��(�A)�`(�J)�̒�����1�I�ׁB�܂��A���̃O���t��I���R���L���B�Ȃ��A�O���t�����₷�����邽�߂ɁA���Ŏ�������l�͂Ȃ߂炩�Ȕj���Ō���ł���B
��(2) ���ɁA����g���M��̐U�������(1)(c)�ŋ��߂�f �ɌŒ肵�A�J�ǂ��p���xω �ʼn�]�������B���̂Ƃ��A��]�ɂ��J���[�̑��x�͉���V���\���ɒx���A���������ɂ͕����Ȃ��B�܂��A�J���[�O����̉��͂Ȃ����̂Ƃ���B
(a) �J�ǂ̒��S����y���Əd�Ȃ�Ƃ��A2�̊J���[�͂��ꂼ�� ��
�� �̈ʒu�ɂ���B���̂Ƃ��̎�����
�̈ʒu�ɂ���B���̂Ƃ��̎����� �Ƃ��A���̂Ƃ�
�Ƃ��A���̂Ƃ� �ɂ������J���[�̑��x��x����
�ɂ������J���[�̑��x��x���� ��y����
��y���� ���A
���A �Cω�Ct ��p���ĕ\���B
�Cω�Ct ��p���ĕ\���B (b) �}�C�N�� �̒����ɔ�ׂ�ƊJ�ǂ���\���ɗ��ꂽx����̓_�Ɉړ������B�J���[���x��x��������
�̒����ɔ�ׂ�ƊJ�ǂ���\���ɗ��ꂽx����̓_�Ɉړ������B�J���[���x��x�������� �������I�ɕω����邽�߁A�h�b�v���[���ʂɂ��J���[������o����鉹�̔g�����܂������I�ɕω�����B�}�C�N�̈ʒu�Ŋϑ�����鉹�̔g���̍ŏ��l�ƍő�l���A
�������I�ɕω����邽�߁A�h�b�v���[���ʂɂ��J���[������o����鉹�̔g�����܂������I�ɕω�����B�}�C�N�̈ʒu�Ŋϑ�����鉹�̔g���̍ŏ��l�ƍő�l���A �Cω�CV��p���ċ��߂�B
�Cω�CV��p���ċ��߂�B (c) ��]����2�̊J���[����̉��g�ɂ́A�h�b�v���[���ʂɂ��U�����̂킸���ȈႢ�����邽�߁A���Ȃ肪������B�U�����̈Ⴂ�͎����I�ɕς��̂ŁA���Ȃ�̉��܂������I�ɕω�����B�}�C�N�̈ʒu�Ŋϑ�����邤�Ȃ�̒P�ʎ��Ԃ�����̉̍ő�l���A �Cω�CV��p���ĕ\���B
�Cω�CV��p���ĕ\���B [��]
��啨��'10�N[3]
������Ԃ̋�C����`��鑬�� �̉��g�ɂ��čl����B�ȉ��̖₢�ɓ�����B
�̉��g�ɂ��čl����B�ȉ��̖₢�ɓ�����B
��1�D�����̋ɂ��Ă͂܂鐔������B
 �}3(a)�̂悤�ɓ_M�ɐÎ~���Ă���U���������ɑ��āA�~�}�Ԃ�����P���
�}3(a)�̂悤�ɓ_M�ɐÎ~���Ă���U���������ɑ��āA�~�}�Ԃ�����P��� (�������A
(�������A )�̑����ŋ߂Â��Ȃ���A���̐U����
)�̑����ŋ߂Â��Ȃ���A���̐U���� �̉����o���Ă���B���Ȃ킿�~�}�Ԃ�1�b�Ԃ�f �̉��g(1�g������1�ƍl����)���Ă���B����킩��̋�����
�̉����o���Ă���B���Ȃ킿�~�}�Ԃ�1�b�Ԃ�f �̉��g(1�g������1�ƍl����)���Ă���B����킩��̋����� �̒n�_��_A�Ƃ���B�_A�Ŕ�����ꂽ���g�������ɓ��B����܂ł̎��Ԃ́A�@�A�@�ł���B�~�}�Ԃ��_A��ʉߌ�A
�̒n�_��_A�Ƃ���B�_A�Ŕ�����ꂽ���g�������ɓ��B����܂ł̎��Ԃ́A�@�A�@�ł���B�~�}�Ԃ��_A��ʉߌ�A �b��ɓ_B�ɗ����B�������A�_B�͓_A�Ɠ_M�̊Ԃɂ���B�_B�Ŕ�����ꂽ���g�������ɓ��B����܂ł̎��Ԃ́A�@�C�@�ł���B����킪�_A����̉��g�����m���Ă���A�_B����̉��g�����m����܂ł̎��Ԃ́A�@�E�@�ƂȂ�B�����@�E�@�̊Ԃɂ�
�b��ɓ_B�ɗ����B�������A�_B�͓_A�Ɠ_M�̊Ԃɂ���B�_B�Ŕ�����ꂽ���g�������ɓ��B����܂ł̎��Ԃ́A�@�C�@�ł���B����킪�_A����̉��g�����m���Ă���A�_B����̉��g�����m����܂ł̎��Ԃ́A�@�E�@�ƂȂ�B�����@�E�@�̊Ԃɂ� �̉��g���܂܂��̂ŁA����킪���肵�����g�̐U�����́A�@�G�@�ƂȂ�B
�̉��g���܂܂��̂ŁA����킪���肵�����g�̐U�����́A�@�G�@�ƂȂ�B
��2�D�����̋ɂ��Ă͂܂鐔������B
 �}3(b)�̂悤�ɒ���P��ɂ���_M���瑪����_O�ɗ������ꍇ���l����B��1�Ɠ������A�~�}�Ԃ͒���P���
�}3(b)�̂悤�ɒ���P��ɂ���_M���瑪����_O�ɗ������ꍇ���l����B��1�Ɠ������A�~�}�Ԃ͒���P��� �̑����ō�����E�Ɉړ����Ȃ���A���̐U����
�̑����ō�����E�Ɉړ����Ȃ���A���̐U���� �̉����o���Ă���B����P��̂���n�_��_C�Ƃ��A����OC�ƒ���P�̂Ȃ��p��
�̉����o���Ă���B����P��̂���n�_��_C�Ƃ��A����OC�ƒ���P�̂Ȃ��p�� �Ƃ���B�~�}�Ԃ��_C��ʉߌ�A
�Ƃ���B�~�}�Ԃ��_C��ʉߌ�A �b��ɓ_D�ɗ����B����OD�̒�����
�b��ɓ_D�ɗ����B����OD�̒����� �Ƃ���B�}3(b)�̂悤�ɐ���OC�ɑ��ē_D����̐����̑���_H�Ƃ���B����
�Ƃ���B�}3(b)�̂悤�ɐ���OC�ɑ��ē_D����̐����̑���_H�Ƃ���B���� ���\���Z���Ƃ��A�pDOC�͏\���������̂ŁA����OD�Ɛ���OH�̒������������ƌ��Ȃ���B���̂��Ƃ𗘗p����ƁA����OC�̒����́A�@�I�@�ƂȂ�B�_C�Ŕ�����ꂽ���g�������ɓ��B����܂ł̎��Ԃ́A�@�J�@�ł���B����킪�_C����̉��g�����m���Ă���A�_D����̉��g�����m����܂ł̎��Ԃ́A�@�L�@�ƂȂ�B�����@�L�@�̊Ԃɂ�
���\���Z���Ƃ��A�pDOC�͏\���������̂ŁA����OD�Ɛ���OH�̒������������ƌ��Ȃ���B���̂��Ƃ𗘗p����ƁA����OC�̒����́A�@�I�@�ƂȂ�B�_C�Ŕ�����ꂽ���g�������ɓ��B����܂ł̎��Ԃ́A�@�J�@�ł���B����킪�_C����̉��g�����m���Ă���A�_D����̉��g�����m����܂ł̎��Ԃ́A�@�L�@�ƂȂ�B�����@�L�@�̊Ԃɂ� �̉��g���܂܂��̂ŁA����킪���肵�����g�̐U�����́A�@�N�@�ƂȂ�B
�̉��g���܂܂��̂ŁA����킪���肵�����g�̐U�����́A�@�N�@�ƂȂ�B
 ��3�D��2�ɂ����āA�U�����̎��ԕω��𑪒��ő��肵���B���肵���U�����̎��ԕω��𐳂����\�����O���t���A�}3(c)�̇@�`�E�̒������I�ׁB�Ȃ��A�e�O���t����2�Ȑ��́A�����̐ݒu�ꏊ������P����߂��ꍇ�Ɖ����ꍇ��\���Ă���A�����̓_
��3�D��2�ɂ����āA�U�����̎��ԕω��𑪒��ő��肵���B���肵���U�����̎��ԕω��𐳂����\�����O���t���A�}3(c)�̇@�`�E�̒������I�ׁB�Ȃ��A�e�O���t����2�Ȑ��́A�����̐ݒu�ꏊ������P����߂��ꍇ�Ɖ����ꍇ��\���Ă���A�����̓_ �͋~�}�Ԃ��_M�Ŕ��������g�������ɓ��B���������ł���B
�͋~�}�Ԃ��_M�Ŕ��������g�������ɓ��B���������ł���B���ɁA����킪����P���牓���ꍇ�̋Ȑ��͋Ȑ�A (����)�A�Ȑ�B (�j��)�̂����ǂ���ł��邩���L���œ�����B
��4�D���ۂ̋~�}�Ԃ́A�u�s�[�|�[�s�[�|�[�E�E�E�E�v�Ƃ����悤�Ɂu�s�[�|�[�v�������̎��ԊԊu �ŌJ��Ԃ������Ă���B��1�̐}3(a)�̂悤�ɋ~�}�Ԃ������ɋ߂Â��Ƃ��ɁA�����ɓ��B����u�s�[�|�[�v���̎��ԊԊu��
�ŌJ��Ԃ������Ă���B��1�̐}3(a)�̂悤�ɋ~�}�Ԃ������ɋ߂Â��Ƃ��ɁA�����ɓ��B����u�s�[�|�[�v���̎��ԊԊu�� �Ƃ��āA���̊W���̒��Ő��������̂��L���œ�����B
�Ƃ��āA���̊W���̒��Ő��������̂��L���œ�����B [��]
���l���啨��'04�N[3]
 �d�͉����x��g�Ƃ��Ď��̖₢�ɓ�����B
�d�͉����x��g�Ƃ��Ď��̖₢�ɓ�����B
(1) ���̕����̋߂�B
���[���Œ肳�ꂽ���� �̌��ɂł�����g�̕���n��(
�̌��ɂł�����g�̕���n��( )�̂Ƃ��̔g���� (a) �ƕ\�����B
)�̂Ƃ��̔g���� (a) �ƕ\�����B �̂Ƃ��̐U���� (b) �ƌĂԁB����`���g�̑����́A����T�ƌ��̒P�ʒ���������̎���(�����x)ρ�Ƃɂ���� (c) �ƕ\�����B
�̂Ƃ��̐U���� (b) �ƌĂԁB����`���g�̑����́A����T�ƌ��̒P�ʒ���������̎���(�����x)ρ�Ƃɂ���� (c) �ƕ\�����B
(2) �����ގ��łł����A�f�ʂ��~�`�Œ��a�̈قȂ�j��A�Ɛj��B������B
�j��A��p���āA�}�̂悤�Ɉ�[��ǂɌŒ肵���[�ɂ͊��Ԃ�ʂ��Ď���m�̂������t����B�ǂƊ��Ԃ̊Ԃ̋����� �ł���B���̒������w�ł͂����ƁA3�̕��̂�����g���ł��āA�U������f�ł������B
�ł���B���̒������w�ł͂����ƁA3�̕��̂�����g���ł��āA�U������f�ł������B (a) �j��A�̐����x�����߂�B
�j��B�ɂ��Ă��}�Ɠ��������ŐU��������ƁA���l��3�̕��̂�����g���ł����B���l�̐ݒ�Őj��A�Ɛj��B�����ׂē����ɂ͂����ƒP�ʎ��Ԃ�����k��̂��Ȃ肪�ϑ�����A�j��B�ɂ�������킸���ɒlj�����ƁA���Ȃ�͏������B���̊ԁA�j��B�̕��̐��͕ω����Ȃ������B
(b) �������lj�����O�ɐj��B�ɐ������g�̐U�����͂����炩�B
(c) �������lj�������A�j��B�ɂ��Ă��邨����̎��ʂ͂����炩�B
(d) �j��B�̒��a�͐j��A�̒��a�̉��{���B [��]
�k�啨��'11�N�O��[3]
�ȉ��̕��͒��� (1) ���� (9) �ɓK�Ȑ����܂��͓��������A (a) �� (b) �ɂ́A�}3�̑I��������K�Ȍ�����I�ыL���œ�����B
 ��1�@�}1�́A�g��
��1�@�}1�́A�g�� �C����
�C���� �̐��ʔg���ォ�猩�����̂ł���B���̔g�́Ay���ɕ��s�ȎR�ƒJ�̔g�ʂ������ʔg�Ƃ��ā{x�����ɐi��ł���B���̏��Ɋϑ��҂����āA�g�����Ă����B
�̐��ʔg���ォ�猩�����̂ł���B���̔g�́Ay���ɕ��s�ȎR�ƒJ�̔g�ʂ������ʔg�Ƃ��ā{x�����ɐi��ł���B���̏��Ɋϑ��҂����āA�g�����Ă����B�ϑ���A���|x�����ɑ��� �Ői��ł����B�g�̑����� (1)
�Ői��ł����B�g�̑����� (1)  �Ȃ̂ŁA�ϑ���A���g�̎R�̏ォ�玟�̎R�̏�ɗ���܂łɂ����鎞��(�ϑ���A���猩������)�� (2)
�Ȃ̂ŁA�ϑ���A���g�̎R�̏ォ�玟�̎R�̏�ɗ���܂łɂ����鎞��(�ϑ���A���猩������)�� (2) 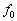 �ƂȂ�B
�ƂȂ�B
���ɁA�ϑ���B���{x�������甽���v���Ɋp�xα (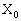 )�̌����ɑ���
)�̌����ɑ���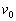 �Ői�Ƃ���A�ϑ���B����͔g���~�܂��Č������B���̂Ƃ��̑�����
�Ői�Ƃ���A�ϑ���B����͔g���~�܂��Č������B���̂Ƃ��̑�����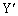 (3)
(3) 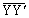 �ł���B
�ł���B
 ��2�@�}2�̂悤�ɁA���[�̈قȂ�̈�T�ƇU�����������E�Ƃ��Đڂ��Ă���B�̈�T��i��ł����g��
��2�@�}2�̂悤�ɁA���[�̈قȂ�̈�T�ƇU�����������E�Ƃ��Đڂ��Ă���B�̈�T��i��ł����g��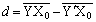 �C����
�C����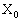 �̕��ʔg���A���E�ɓ��ˊpθ �œ��˂��A���܂����B�̈�U�ɂ�����g�̑�����
�̕��ʔg���A���E�ɓ��ˊpθ �œ��˂��A���܂����B�̈�U�ɂ�����g�̑�����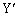 �ł���Ƃ��A���̔g���� (4)
�ł���Ƃ��A���̔g���� (4) 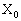 �ƂȂ�B���܊p
�ƂȂ�B���܊p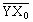 �͊W�� (5) �ɂ�茈�܂�B
�͊W�� (5) �ɂ�茈�܂�B���ɐ}3�̂悤�ɁA���E��ȕǂƂ��A�������ˊpθ �̔g�˂������B���̂Ƃ��A���˔g�͓��˔g�Ɠ��������� (a) �̌����ɐi�ށB���������āA���˔g�Ɣ��˔g�̎R�̔g�ʂ���������_A�́A (b) �̌����ɓ����B
 ��3�@�}4�̂悤�ɁA2�̃X���b�g��������ȕǂɁA�g��
��3�@�}4�̂悤�ɁA2�̃X���b�g��������ȕǂɁA�g��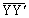 �̐��ʔg�����ˊp
�̐��ʔg�����ˊp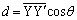 �œ��˂����B�g�͊e�X���b�g����ǂ̉E���ɋ��ʔg�Ƃ��čL�������B�e�X���b�g�̕��͋����A�ȉ��ł͕�������B�Ȃ��A2�̃X���b�g�̊Ԋu��
�œ��˂����B�g�͊e�X���b�g����ǂ̉E���ɋ��ʔg�Ƃ��čL�������B�e�X���b�g�̕��͋����A�ȉ��ł͕�������B�Ȃ��A2�̃X���b�g�̊Ԋu��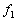 �ŁA�ǂ̗����Ŕg�̑����͓��������̂Ƃ���B
�ŁA�ǂ̗����Ŕg�̑����͓��������̂Ƃ���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B