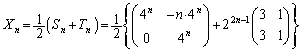愛媛大理数学'08年[5]
行列A,E,Oを
とする。ここで、a,b,c,dは実数で、ある実数kに対して、
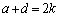 ,
,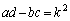
(1) 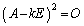 を示せ。
を示せ。 (2) 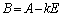 とおく。自然数nに対して、
とおく。自然数nに対して、 が成り立つことを示せ。
(3) 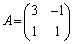 のとき、
のとき、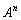 (nは自然数)を求めよ。
(nは自然数)を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 固有値重解型の行列の累乗の問題です。素直に対角化したり、スペクトル分解したりするのでは解決できないので、特殊な技巧が必要になります。本問では、(2)でその技巧が提示されていて、(2)を利用して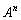 を求めることになります。
を求めることになります。
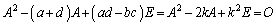 ・・・①
・・・①よって、
(Ⅰ) 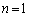 のとき、
のとき、 より、成り立ちます。
(Ⅱ) 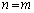 のとき、
のとき、 が成り立つと仮定します。この両辺に左からAをかけて、
①より、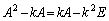 なので、
なので、 よって、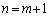 のときにも成り立ちます。
のときにも成り立ちます。 (Ⅰ),(Ⅱ)より、自然数nに対して、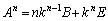 が成り立ちます。
が成り立ちます。
別解 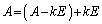 と書けて、
と書けて、 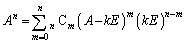 ・・・②
・・・②(1)より、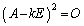 なので、
なので、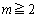 のとき、
のとき、 です。これより、②では、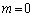 ,
,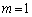 のところだけが生き残って、
のところだけが生き残って、
(3) 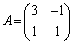 のとき、ハミルトン・ケーリーの定理より、
のとき、ハミルトン・ケーリーの定理より、 となるので、(1)の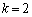 の場合になります。
の場合になります。 また、(2)の結果で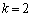 とすることにより、
とすることにより、 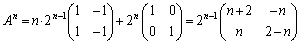 ......[答]
......[答]
追記.固有値重解型の行列の累乗の問題を初めて見る受験生には、(2)の別解は、あまりに技巧的と映るかも知れませんが、最近少なくなったとは言っても、ポピュラーで古典的な技巧なので、スペクトル分解の形と見比べながら頭に入れておいてください。例えば、早大理工'92[1]:
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
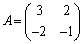 とする。条件
とする。条件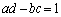 ,
,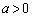 をみたす整数a,b,c,dを成分とする行列
をみたす整数a,b,c,dを成分とする行列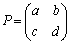 を適当に選ぶとき、
を適当に選ぶとき、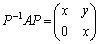 が成り立つ。このとき、
が成り立つ。このとき、
(1) x,yを求めよ。
(2) 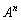 (
(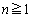 )を求めよ。
)を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
では、(1)は、実質的に整数問題なので、
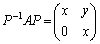 の左からPをかけて、
の左からPをかけて、
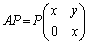
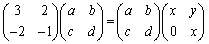
∴ 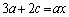 ,
,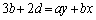 ,
,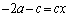 ,
,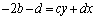 ・・・①
・・・①
第3式より、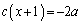 ・・・②
・・・②
これを第1式×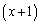 に代入すると、
に代入すると、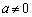 より、
より、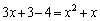
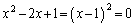
∴ 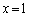 ......[答]②より、
......[答]②より、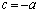
①の第4式より、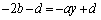 ,
,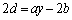
これと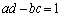 より、
より、
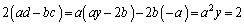
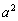 とyは2の約数ですが、
とyは2の約数ですが、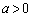 より、こうなるのは、
より、こうなるのは、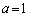 ,
,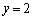 のときのみです。
のときのみです。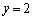 ......[答]
......[答]
ハミルトン・ケーリーの定理より、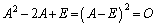 ・・・③
・・・③
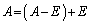 として、二項定理より、
として、二項定理より、
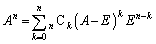
③より、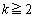 では、
では、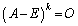 となるので、
となるので、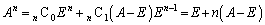
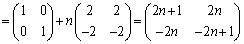 ......[答]
......[答] とするべきです。
さて、2008年度の入試問題で、言わば「行列の漸化式」を考えるようになっている問題が目に付くので、まとめておくことにします。以下、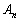 ,B,C,D,P,Qを2次の正方行列、Eを2次の単位行列として考えることにします。
,B,C,D,P,Qを2次の正方行列、Eを2次の単位行列として考えることにします。
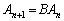
という漸化式は、言ってみれば、公比Bの等比「行列」列のようなものですが、これは、数列と同じく、一般項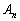 は
は
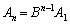
です。
2項間漸化式:
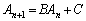 ・・・①
・・・①
は、数列の場合と同様に、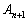 と
と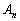 をDに置き換えた
をDに置き換えた
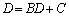 ・・・②
・・・②
を考えると、
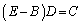
従って、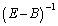 が存在すれば、
が存在すれば、
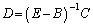
として、①-②を作ると、
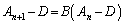
「行列」列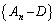 は、公比Bの等比「行列」列なので、
は、公比Bの等比「行列」列なので、
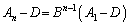
∴ 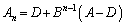
となり、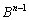 を行列の累乗の問題として求めれば、数列の場合と全く同様にして解答できます。
を行列の累乗の問題として求めれば、数列の場合と全く同様にして解答できます。
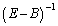 が存在しない場合は、数列の場合のようには行きません。
が存在しない場合は、数列の場合のようには行きません。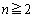 として、①の項番号を1つずつ小さくしてBを順次かけた式を作り、
として、①の項番号を1つずつ小さくしてBを順次かけた式を作り、
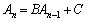
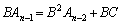
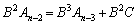
・・・・・・
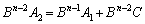
これらを足し合わせると、両辺の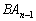 ,
,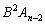 ,・・・,
,・・・,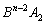 が消し合って、
が消し合って、
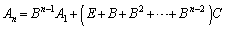 (
(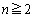 )
)
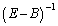 が存在しないとき、Bは固有値1をもっています。もう1つの固有値をuとして
が存在しないとき、Bは固有値1をもっています。もう1つの固有値をuとして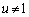 であれば、
であれば、
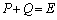 ,
,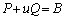
を解き、
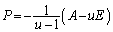 ,
,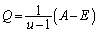 ,
,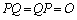 ,
,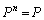 ,
,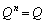
(スペクトル分解を参照)より、
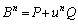
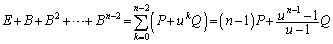 (
(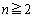 )
)
∴ 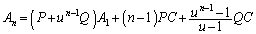 (
(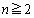 )
)
となります。
固有値1が重解になっている(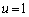 )場合は、本問愛媛大(2)の結果を用いて、
)場合は、本問愛媛大(2)の結果を用いて、
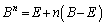
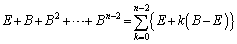
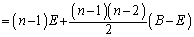
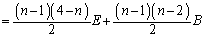
∴ 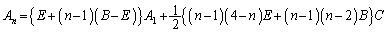
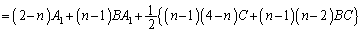 (
(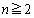 )
)
3項間漸化式:
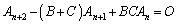 ・・・③
・・・③
では、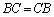 かつ
かつ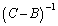 が存在すれば、③を、
が存在すれば、③を、
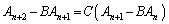 ・・・④
・・・④
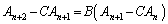 ・・・⑤
・・・⑤
と2通りに書き換えて、
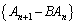 が公比Cの「行列」列であることから、
が公比Cの「行列」列であることから、
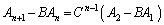 ・・・⑥
・・・⑥
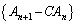 が公比Bの「行列」列であることから、
が公比Bの「行列」列であることから、
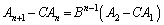 ・・・⑦
・・・⑦
⑥-⑦として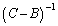 を左からかけることにより、
を左からかけることにより、
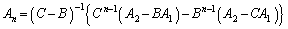
と、数列と同様に求めることができます。
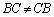 のときには⑤は作れますが④が成立しません。⑦は使えるので、
のときには⑤は作れますが④が成立しません。⑦は使えるので、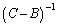 が存在しない場合も含めて以下のようにします(このタイプの問題は、山口大医'08年[4]を参照)。
が存在しない場合も含めて以下のようにします(このタイプの問題は、山口大医'08年[4]を参照)。
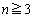 として、⑦の項番号を1つずつ小さくしてCをかけた式を順次作り、
として、⑦の項番号を1つずつ小さくしてCをかけた式を順次作り、
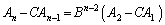
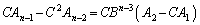
・・・・・・
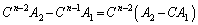
これらを足し合わせると、左辺の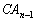 ,
,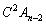 ,・・・,
,・・・,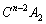 が消し合って、
が消し合って、
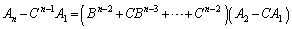
∴ 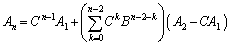 (
(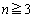 )
)
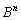 ,
,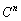 の形を求めれば、
の形を求めれば、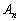 を求めることができます。
を求めることができます。
以下に2項間漸化式の場合の問題例を挙げます。
金沢大理工'08年前期[1]:
自然数nに対して、2次正方行列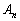 を
を
により定める。また、2次正方行列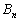 は
は
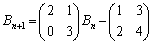 (
(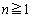 )
)
(1) 数学的帰納法を用いて
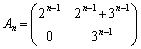 (
(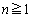 )
)が成り立つことを示せ。
(2) ある2次正方行列Cに対して、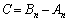 がすべてのnについて成り立つとする。このとき、Cを求めよ。
がすべてのnについて成り立つとする。このとき、Cを求めよ。 (3) (2)の条件をみたす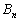 のうち、逆行列をもたないものは
のうち、逆行列をもたないものは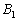 に限ることを示せ。
に限ることを示せ。
解答
(1) (Ⅰ) 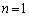 のとき、
のとき、 より成り立ちます。
(Ⅱ) 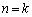 のとき、
のとき、 が成り立つと仮定します。
より、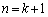 のときも成り立ちます。
のときも成り立ちます。 (Ⅰ),(Ⅱ)より、
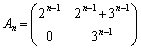 (
(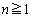 )
)が成り立ちます。
注.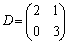 として、ハミルトン・ケーリーの定理より、
として、ハミルトン・ケーリーの定理より、 より、Dの固有値は2と3で、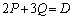 ,
,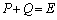 を連立すると、
を連立すると、 ここからも、
となります。
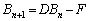 ・・・①
・・・①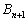 と
と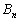 をGと置き換えた式
をGと置き換えた式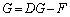 ・・・②
・・・②より、
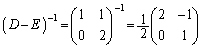 を左からかけて、
を左からかけて、①-②より、
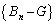 は(1)の
は(1)の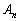 と全く同じ形の漸化式に従っています。
と全く同じ形の漸化式に従っています。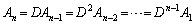 ・・・③
・・・③となるので、同様に、
∴ 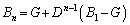 ・・・④
・・・④ 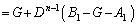 ・・・⑤
・・・⑤⑤がすべてのnについて成り立つとすれば、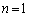 においても成り立つので、
においても成り立つので、 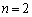 においても成り立つので、
においても成り立つので、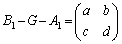 として、
として、∴ 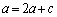 ,
,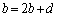 ,
,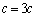 ,
,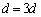
これらを満たすa,b,c,dは、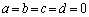 のみで、
のみで、 ∴ 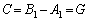 逆に、
逆に、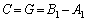 のとき、すべてのnについて⑤が成り立ちます。
のとき、すべてのnについて⑤が成り立ちます。
∴ 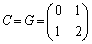 ......[答]
......[答]
(3) (2)より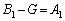 なので、④において、
なので、④において、 ③より、
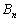 の行列式は、
の行列式は、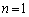 のとき、
のとき、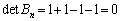
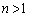 のとき、
のとき、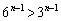 ,
,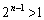 より、
より、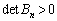
よって、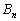 の中で逆行列をもたないものは
の中で逆行列をもたないものは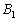 に限ります。
に限ります。
阪大理系'08年前期[1]:
2次の正方行列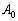 ,
,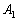 ,
,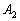 ,
,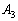 ,・・・を
,・・・を
で定める。ただし、Oは2次の零行列、BとCは2次の正方行列とする。
(1) 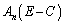 をBとCを用いて表せ。ここでEは2次の単位行列とする。
をBとCを用いて表せ。ここでEは2次の単位行列とする。 (2) BとCを
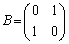 ,
,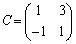
とするとき、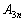 を求めよ。
を求めよ。
解答 Cの累乗に規則性があるので、この問題は誘導通りに解答します。
(1) 与えられた漸化式を用いて、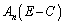 を計算してみます。
を計算してみます。 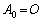 なので、
なので、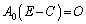 ・・・①
・・・①これより、
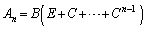 (
(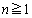 )
)と予測できます。
(Ⅰ) 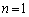 のとき、②より予測は成り立ちます。
のとき、②より予測は成り立ちます。 (Ⅱ) 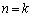 のとき、予測が成り立つとして、
のとき、予測が成り立つとして、 (Ⅰ),(Ⅱ)より、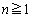 において予測は成り立ちます。
において予測は成り立ちます。
∴ 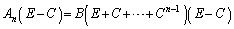
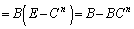 ......[答]
......[答]
(2) (1)の結果の中にCの累乗が出てくるので、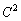 ,
,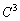 ,・・・ を調べてみます。
,・・・ を調べてみます。 従って、nを0以上の整数として、
(1)より、
右から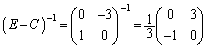 をかけて、
をかけて、 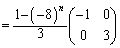 ......[答]
......[答]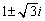 )になり、うまく行きません(高校範囲外であれば行列の成分に虚数が出てきてもよいのですが)。
)になり、うまく行きません(高校範囲外であれば行列の成分に虚数が出てきてもよいのですが)。
広島県大'08年[5]:
条件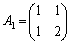 ,
,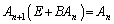 (
(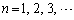 )で定められる2次の正方行列
)で定められる2次の正方行列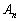 を考える。ここで、
を考える。ここで、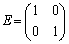 ,
,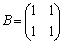 である。
である。
(1) 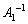 を求めよ。
を求めよ。
(2) 数学的帰納法により、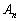 は逆行列をもつことを示せ。
は逆行列をもつことを示せ。
(3) 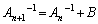 を示せ。
を示せ。
(4) 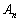 を求めよ。
を求めよ。
解答 数列であれば、
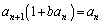
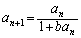
という漸化式で、両辺の逆数を考え、
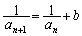
とすると、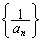 が等差数列になる、というタイプのものです。
が等差数列になる、というタイプのものです。
行列では、逆行列を考えると等差数列と類似の形が出てきます。
(1) 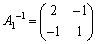 ......[答]
......[答]
(2) (Ⅰ) 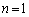 のとき、(1)より
のとき、(1)より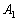 は逆行列をもちます。
は逆行列をもちます。 問題文の漸化式で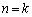 として、
として、 右から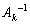 をかけると、
をかけると、 これは、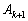 の逆行列が
の逆行列が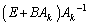 であることを意味します。 ・・・①
であることを意味します。 ・・・①
よって、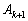 も逆行列をもちます。
も逆行列をもちます。 (Ⅰ),(Ⅱ)より、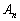 は逆行列をもちます。
は逆行列をもちます。
(3) ①より、
(4) (3)の結果を繰り返して使うことにより、
∴ 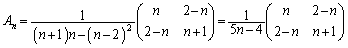 ......[答]
......[答]
九州工大工'08年前期[3]:
行列A,B,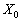 ,
,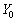 を
を
とする。2次の正方行列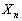 ,
,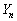 (
(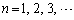 )を
)を
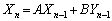 ,
,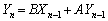
(1) 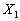 ,
,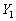 を求めよ。
を求めよ。 (2) 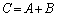 とする。すべての自然数nに対して
とする。すべての自然数nに対して が成り立つことを数学的帰納法によって示せ。
(3) 自然数nに対して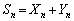 とおく。
とおく。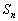 を求めよ。
を求めよ。 (4) 自然数nに対して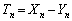 とおく。
とおく。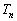 を求めよ。
を求めよ。 (5) 自然数nに対して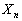 を求めよ。
を求めよ。
解答 行列の連立漸化式ですが、数列の連立漸化式と同じ感覚でできます。
(1) 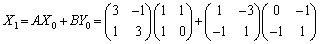
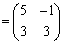 ......[答]
......[答]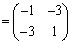 ......[答]
......[答]
(2) 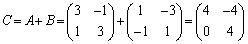
(Ⅰ) 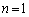 のとき、
のとき、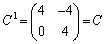 より成り立ちます。
より成り立ちます。 (Ⅱ) 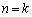 のとき、
のとき、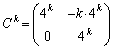 が成り立つと仮定します。
が成り立つと仮定します。 よって、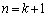 のときも成り立ちます。
のときも成り立ちます。 (Ⅰ),(Ⅱ)より、すべての自然数nに対して、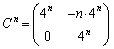 が成り立ちます。
が成り立ちます。
(3) 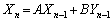 ・・・①
・・・① 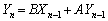 ・・・②
・・・②①+②より、
(4) ①-②より、
(3)と同様にして、
(5) 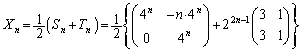
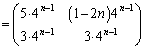 ......[答]
......[答]
数学TOP TOPページに戻る
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。