�����吔�w'11�N[2]
���ʏ�ɐ��O�p�`�łȂ��s�p�O�p�`ABC���^�����Ă���B��BC�CCA�CAB�̒��������ꂼ��a�Cb�Cc�Ƃ��A �Ƃ����B��BC�CCA�CAB�����ꂼ��
�Ƃ����B��BC�CCA�CAB�����ꂼ�� �F
�F �C
�C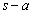 �F
�F �C
�C �F
�F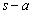 �ɓ�������_��X�CY�CZ�Ƃ���B�܂��AO�����_�Ƃ���B���̖₢�ɓ�����B
�ɓ�������_��X�CY�CZ�Ƃ���B�܂��AO�����_�Ƃ���B���̖₢�ɓ�����B
��1�@�_N�� �ƒ�`����Ƃ��A3����AX�CBY�CCZ��N�Ō���邱�Ƃ������B
�ƒ�`����Ƃ��A3����AX�CBY�CCZ��N�Ō���邱�Ƃ������B ��2�@P����ABC�̓����̓_�A��PBC�C��PCA�C��PAB�̖ʐς����ꂼ�� �C
�C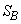 �C
�C �Ƃ���Ƃ��A
�Ƃ���Ƃ��A �ƕ\�����B���̂��Ƃ�p���āA��ABC�̊O�S��Q�Ƃ���Ƃ��A ��
�� �C
�C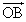 �C
�C �Ca�Cb�Cc��p���ĕ\���B
�Ca�Cb�Cc��p���ĕ\���B ��3�@��ABC�̏d�S��G�Ƃ���B�_N��Q��G��ʂ钼����ɂ���Ƃ��A��ABC�͓ӎO�p�`�ł��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��3�͐��܂����v�Z�ɂȂ�܂��B�Ђ�����n���ɂ�邵���Ȃ������ł��B
��1�@
�ƂȂ�̂ŁA�`�F�o�̒藝�̋t���A3����AX�CBY�CCZ�́A1�_M�Ō����܂��B���l���E�X�̒藝���A  �@�� ZM�FMC =
�@�� ZM�FMC =  �Fc
�Fc����āAM��ZC��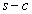 �Fc�ɓ�������_�ł��B
�Fc�ɓ�������_�ł��B �ƂȂ�̂ŁA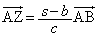 ���A
���A ����A
�@�C�A���AM��N�͈�v���A3����AX�CBY�CCZ��N�Ō����܂��B
����āAB�CN�CY�͈꒼����̓_�ł��B
����āAC�CN�CZ�͈꒼����̓_�ł��B
�ȏ���A3����AX�CBY�CCZ��N�Ō����܂��B
��2�@��蕶����
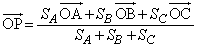 �@���(��)
�@���(��)���Ă����܂��BAP�̉�����BC�Ƃ̌�_��L�Ƃ��܂��BL�́ABC��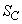 �F
�F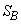 �ɓ�������_�ł��B����āA
�ɓ�������_�ł��B����āA P�́AAL��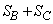 �F
�F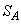 �ɓ�������_�ł��B����āA
�ɓ�������_�ł��B����āA  �C
�C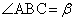 �C
�C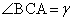 �Ƃ���ƁA���S�p�͉~���p��2�{�ɂȂ�̂ŁA
�Ƃ���ƁA���S�p�͉~���p��2�{�ɂȂ�̂ŁA
 �C
�C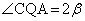 �C
�C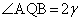
��ABC�̊O�ډ~�̔��a��R�Ƃ���ƁA��QBC�C��QCA�C��QAB�̖ʐ� �C
�C �C
�C �́A
�́A���l�ɁA
�ȏ���A(��)��p���āA
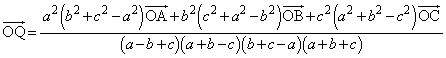 ......[��]
......[��]
��3�@��2���A
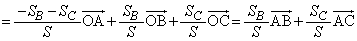 �@(��
�@(�� 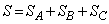 )
)�A��p���āA
�_N��Q��G��ʂ钼����ɂ���Ƃ��Ak�������Ƃ��āA ���A
���A  �C
�C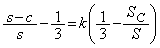
�������k���������āA
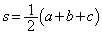 �C
�C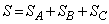 ���A
���A�W�J���Đ�������ƁA
�B��p���āA
������āA
��1���̃J�b�R���́A
��2���̒��J�b�R���́A
����āA
�J�b�R�������āA
���J�b�R���� �Ŋ���ƁA�����āA���́A
�Ŋ���ƁA�����āA���́A �@(�����藝���Q��)
�@(�����藝���Q��) ���������� �Ŋ���ƁA�����āA���́A
�Ŋ���ƁA�����āA���́A �C���ǁA
�C���ǁA 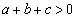 ���A
���A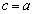 �܂���
�܂���  �܂���
�܂��� 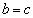 ����āA��ABC�͓ӎO�p�`�ł��B
����āA��ABC�͓ӎO�p�`�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 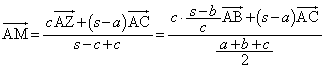
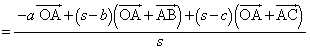
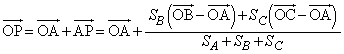
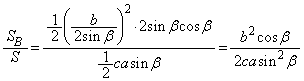
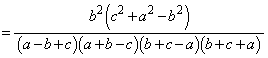
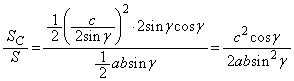

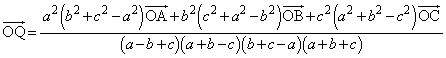 ......[��]
......[��]