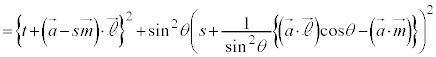��嗝�n���w'24�N�O��[3]
��ԓ���2����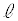 �Cm�͂˂���̈ʒu�ɂ���Ƃ���B
�Cm�͂˂���̈ʒu�ɂ���Ƃ���B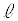 ��m�̗����ɒ������钼��������1���݂��邱�Ƃ������B
��m�̗����ɒ������钼��������1���݂��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���嗝�n24�N[3]�Ɠ����悤�Ȗ��ł����A������͏ؖ����ɂȂ��Ă��܂��B
�u���݂���v���Ƃ̏ؖ��́A�ǂ�����Α�ӂ̂��̂��邩�A���̎菇��������邱�Ƃɂ���čs�����Ƃ��ł��܂��B�ȉ��ł́A���̉�@�ƁA2������̓_�̍ŒZ������^����2�_�����Ԓ���������2�����ɐ����ɂȂ�Ƃ��������Ɋ�Â����@�ƁA2�ʂ�̕��@�ʼn��Ă݂܂��B�Ȃ��A��ԃx�N�g�����Q�Ƃ��Ă��������B
[��@1]�@��ԓ���2�̃x�N�g��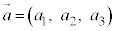 �C
�C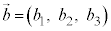 ���A1���Ɨ��A�܂�A
���A1���Ɨ��A�܂�A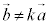 ����
����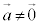 ����
����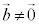 ���Ƃ��܂��B
���Ƃ��܂��B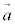 �C
�C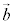 ���O��
���O��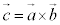 �́A
�́A
�ƂȂ�܂��B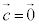 �Ƃ���ƁA
�Ƃ���ƁA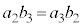 �C
�C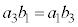 �C
�C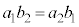 �ƂȂ�A
�ƂȂ�A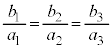 (
(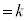 )�C
)�C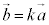 �ƂȂ��Ă��܂��̂ŁA
�ƂȂ��Ă��܂��̂ŁA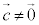 �ł��B
�ł��B
�ƂȂ�̂�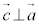 (�������Q��)�C���l�ɁA
(�������Q��)�C���l�ɁA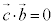 �ƂȂ�̂�
�ƂȂ�̂�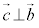 �ŁA
�ŁA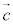 (
(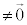 )��
)��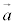 �C
�C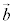 �̑o���ɐ����ȃx�N�g���ł��B
�̑o���ɐ����ȃx�N�g���ł��B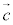 ��
��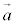 ��
��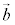 �Œ��镽�ʏ�̃x�N�g���łȂ����Ƃ͖��炩�ł����A�m���߂Ă����ƁA���ɁAs�Ct�������Ƃ��āA
�Œ��镽�ʏ�̃x�N�g���łȂ����Ƃ͖��炩�ł����A�m���߂Ă����ƁA���ɁAs�Ct�������Ƃ��āA
�Ƃ������Ƃ��܂��B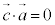 ���A
���A
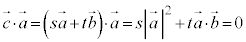 �C
�C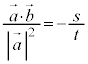
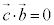 ���A
���A
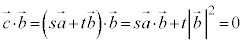 �C
�C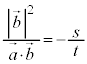
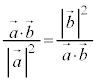 �@��
�@�� 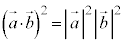
 ��
�� �̂Ȃ��p��θ�Ƃ��āA
�̂Ȃ��p��θ�Ƃ��āA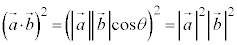
�@�� 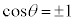 �C
�C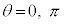
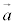 ��
��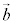 ��1���Ɨ��łȂ��Ȃ�̂ŁA
��1���Ɨ��łȂ��Ȃ�̂ŁA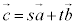 �Ƃ������Ƃ͂ł����A
�Ƃ������Ƃ͂ł����A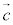 ��
��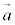 ��
��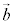 �Œ��镽�ʏ�̃x�N�g���ł͂Ȃ��A
�Œ��镽�ʏ�̃x�N�g���ł͂Ȃ��A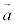 �C
�C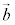 �C
�C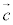 ��1���Ɨ��ł��B�@���(��)
��1���Ɨ��ł��B�@���(��)
��ԓ���2����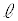 �Cm�͂˂���̈ʒu�ɂ���̂ŁA2����
�Cm�͂˂���̈ʒu�ɂ���̂ŁA2����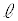 �Cm�̕����x�N�g��
�Cm�̕����x�N�g��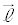 �C
�C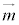 �͕��s�ł͂Ȃ�����x�N�g���łȂ��A
�͕��s�ł͂Ȃ�����x�N�g���łȂ��A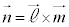 (
(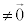 )�Ƃ���ƁA(��)���A
)�Ƃ���ƁA(��)���A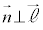 �C
�C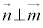 �ł����āA
�ł����āA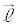 �C
�C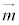 �C
�C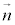 ��1���Ɨ��ł��B����
��1���Ɨ��ł��B����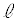 ���܂�
���܂�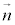 �ɕ��s��������α�Ƃ��܂��B
�ɕ��s��������α�Ƃ��܂��B
����α�́A����m�Ƃ���1�̌�_P�������܂�(��_�������Ȃ���A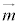 //α�ƂȂ�A
//α�ƂȂ�A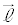 �C
�C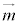 �C
�C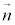 ��1���Ɨ��ł��邱�Ƃɔ����܂��B�܂��A���ʂƒ����������̌�_�������Ƃ͂���܂���)�B
��1���Ɨ��ł��邱�Ƃɔ����܂��B�܂��A���ʂƒ����������̌�_�������Ƃ͂���܂���)�B
P��ʂ�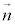 ������x�N�g���Ƃ��钼���́A����α���̒����ł����āA����
������x�N�g���Ƃ��钼���́A����α���̒����ł����āA����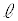 �Ƃ���1�̌�_Q�������܂�(��_�������Ȃ���A
�Ƃ���1�̌�_Q�������܂�(��_�������Ȃ���A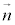 //
//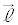 �ƂȂ�
�ƂȂ�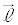 �C
�C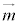 �C
�C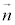 ��1���Ɨ��ł��邱�Ƃɔ����܂��B�܂�2�����������̌�_�������Ƃ͂���܂���)�B
��1���Ɨ��ł��邱�Ƃɔ����܂��B�܂�2�����������̌�_�������Ƃ͂���܂���)�B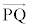 //
//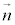 �ł���A
�ł���A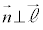 �C
�C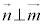 ���A
���A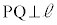 �C
�C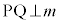 ���A
���A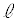 ��m�̗����ɒ������钼��������1���݂��܂��B
��m�̗����ɒ������钼��������1���݂��܂��B
[��@2]�@��q��������1�̍l�����ʼn��܂��B
�v�Z���ȒP�ɂ��邽�߁A����m�����_��ʂ�悤�ɑS�̂s�ړ����A����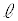 �Cm�̕����x�N�g��
�Cm�̕����x�N�g��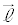 �C
�C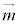 ��
��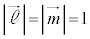 �����A���x�N�g���̂Ȃ��p��θ�C�܂�A
�����A���x�N�g���̂Ȃ��p��θ�C�܂�A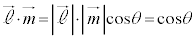 ���Ƃ��܂��B2����
���Ƃ��܂��B2����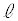 �Cm�͂˂���̈ʒu�ɂ���̂�
�Cm�͂˂���̈ʒu�ɂ���̂�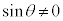 �ł��B����
�ł��B����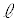 ���1�_���w���x�N�g����
���1�_���w���x�N�g����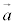 �Ƃ���ƁA��ԓ���2�����̃x�N�g�����������A
�Ƃ���ƁA��ԓ���2�����̃x�N�g�����������A
�ƕ\�����Ƃ��ł��܂��B����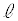 ��̓_�ƒ���m��̓_�̋�����2��́A
��̓_�ƒ���m��̓_�̋�����2��́A
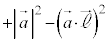 �@(
�@(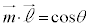 )
)
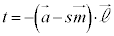 ����
����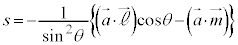 �@���(����)
�@���(����)
����āA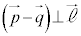 �ł��B�@����@
�ł��B�@����@
������(����)���A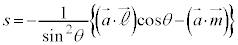 �C�����������ƁA
�C�����������ƁA
����āA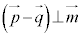 �ł��B�@����A
�ł��B�@����A
����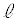 ��̓_�ƒ���m��̓_�̋����̍ŏ��l��^����t�Cs��(����)�̂���1�ő��݂��A���̂Ƃ�����
��̓_�ƒ���m��̓_�̋����̍ŏ��l��^����t�Cs��(����)�̂���1�ő��݂��A���̂Ƃ�����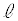 ��̓_�ƒ���m��̓_�����Ԓ����͂���1�ɒ�܂�܂��B���̒����́A�@�C�A���A����
��̓_�ƒ���m��̓_�����Ԓ����͂���1�ɒ�܂�܂��B���̒����́A�@�C�A���A����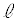 �ƒ���m�̑o���ɐ����ł��B�����A
�ƒ���m�̑o���ɐ����ł��B�����A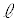 ��m�̗����ɒ������钼��������1���݂��܂��B
��m�̗����ɒ������钼��������1���݂��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 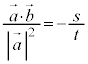
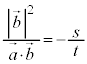
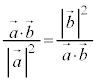 �@��
�@��