慶大理工数学'09年[A1]
(1) 平面上において点Oを中心とする半径rの円を考える。この円の外部にある点Aからこの円に引いた2本の接線のなす角度が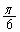
であるとき、
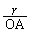の値は ア である。 (2) xy平面上で放物線C：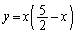
と直線l：
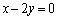が囲む図形の面積は イ である。放物線Cと直線lとの2つの交点をA，Bとする。点Pが放物線上をAからBまで動くとき、三角形APBの面積が最大となるのは点Pが
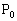( ウ ， エ )のときである。点
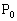から直線lにおろした垂線を
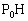とすると、Hの座標は( オ ， カ )である。 (3) xy平面上において曲線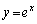
および2つの直線
，
，
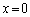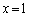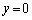により囲まれる図形をKとする。図形Kをx軸のまわりに回転してできる立体の体積は キ であり、図形Kをy軸のまわりに回転してできる立体の体積は ク である。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 深くは聞かないけれど、一通りのことは確かめておこうという基本問題3題です。(1)については、解答を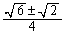
としているウェブサイトもあります。確かにそうなのですが、でもそれが正解なのだとしたら、出題者の品位を疑いたくなります。
(1)(ア)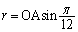 
∴ 
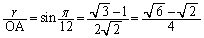......[答]
(2)(イ) C：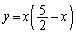
l：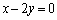
両式を連立し、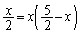
∴ 
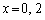
Cとlで囲む図形の面積Sは、 (ウ) 三角形APBの面積が最大になるのは、点PにおけるCの接線がlと平行になるとき(2直線の平行・垂直を参照)です。 C：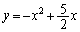
について、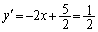 
(
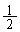は、lの傾き)のとき、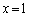
......[答] (エ)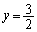 
これとl：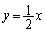
とを連立して、 ∴ 
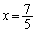......[答] (カ)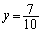 
......[答]
(3)(キ) 図形Kをx軸のまわりに回転してできる立体の体積は、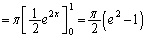 
......[答](ク) 図形Kをy軸のまわりに回転してできる立体の体積は、底面が半径1の円で高さeの円柱の体積から、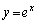
とy軸，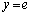
で囲まれる図形をy軸のまわりに回転してできる立体の体積を引いたもので、
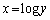より、
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
......[答]
)
