�c�嗝�H���w'10�N[A1]
(1) ���ʏ��2�̃x�N�g��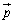 �C
�C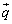 ��
��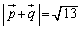 �C
�C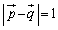 �C
�C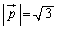 �����Ă���B���̂Ƃ��A
�����Ă���B���̂Ƃ��A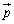 ��
��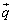 �̓���
�̓���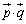 ��
��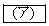 �ł���A
�ł���A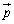 ��
��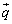 �̂Ȃ��pθ ��
�̂Ȃ��pθ ��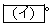 �ł���B�������A
�ł���B�������A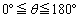 �ł���B
�ł���B (2) ��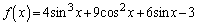 ��
��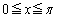 �ɂ�����ŏ��l��
�ɂ�����ŏ��l��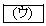 �ł���A�ő�l��
�ł���A�ő�l��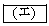 �ł���B
�ł���B (3) ����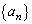 ��
�� �����Ă���B���̐���̈�ʍ��́A �ŗ^������B
�ŗ^������B
�܂��A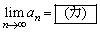 �ł���B
�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��������A���ȏ��̗�背�x���̊�{���ł��B��[�`���Ȃ̂ŁA�P�A���X�E�~�X�͒v�����ł��B
(1)(�A) 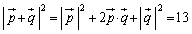 �@����@�@(�������Q��)
�@����@�@(�������Q��) 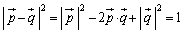 �@����A
�@����A�@�|�A���A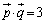 ......[��]
......[��] (�C) 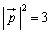 �Ƈ@���A
�Ƈ@���A �� 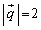
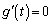 �Ƃ���ƁA
�Ƃ���ƁA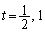
�����\���A�ŏ��l��6 ......[��] (�G) �ő�l��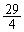 ......[��]
......[��]
(3)(�I) �^����ꂽ�Q�����ŁA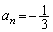 �Ƃ���ƁA���ӂ�
�Ƃ���ƁA���ӂ�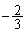 �ƂȂ�̂ɁA�E�ӂ�0�Ȃ̂ŁA
�ƂȂ�̂ɁA�E�ӂ�0�Ȃ̂ŁA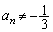 �ł��B�����ŁA�^����ꂽ�Q������
�ł��B�����ŁA�^����ꂽ�Q������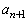 �ɂ��ĉ����ƁA
�ɂ��ĉ����ƁA 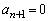 �Ƃ����
�Ƃ����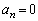 �ł����A
�ł����A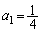 �Ȃ̂ŁA
�Ȃ̂ŁA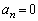 �ƂȂ�n�͂���܂���B�����ŁA���ӂ̋t�����l���A
�ƂȂ�n�͂���܂���B�����ŁA���ӂ̋t�����l���A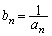 �Ƃ����ƁA
�Ƃ����ƁA�� 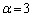 �B�|�C���A
�B�|�C���A ������A����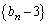 �́A����
�́A����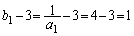 �C����
�C����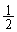 �����䐔���B
�����䐔���B �� 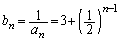 ��
�� 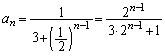 ......[��]
......[��] �� 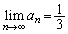 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  ......[��]
......[��]