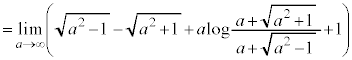���嗝�n���w'24�N�O��[5]
a��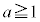 �����萔�Ƃ���B���W���ʏ�ŁA����4�̕s�������\���̈��
�����萔�Ƃ���B���W���ʏ�ŁA����4�̕s�������\���̈��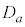 �Ƃ���B
�Ƃ���B
���̖₢�ɓ�����B
(1) 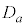 �̖ʐ�
�̖ʐ�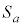 �����߂�B
�����߂�B
(2)  �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ʐς͘r�Â��Ōv�Z���邵������܂��A�Ɍ��́A���X�H�v���K�v�ł��B
 �̈�
�̈�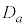 �͉E�}���ΐF���F���ł��B
�͉E�}���ΐF���F���ł��B
�Ȑ�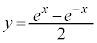 �ƒ���
�ƒ���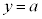 �Ƃ̌�_�́A
�Ƃ̌�_�́A
�� 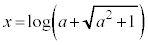 �@(�ΐ������Q��)
�@(�ΐ������Q��)
�Ȑ�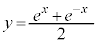 �ƒ���
�ƒ���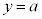 �Ƃ̌�_�́A
�Ƃ̌�_�́A
�� 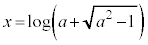
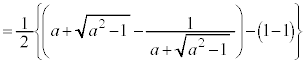 �@(
�@(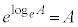 �ɒ���)
�ɒ���)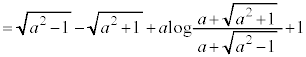 ......[��]
......[��]���D���Ă������Ƃ��ɁA��L�ł́A��ϕ��̏�[�Ɖ��[�����G�œ��Ă������ɂ����Ȃ�̂��v�Z�O���疾�炩�Ȃ̂ŁA��[�Ɖ��[���ɂ����ē��Ă����������悢�Ǝv���܂��B
�����ŁA
�Ƃ�����ɂȂ�܂��B
(2) 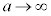 �̂Ƃ��A
�̂Ƃ��A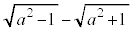
�܂��A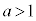 �̂Ƃ��A
�̂Ƃ��A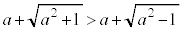 �C
�C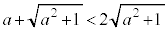 �C
�C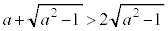
����āA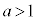 �Ƃ��āA
�Ƃ��āA 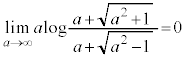 �@����A
�@����A(1)�̌��ʂɂ����āA�@�C�A���A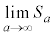
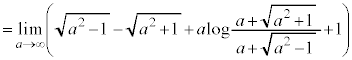
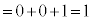 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 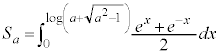
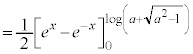
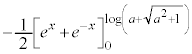
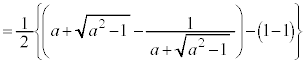 �@(
�@(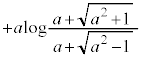
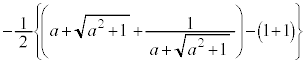
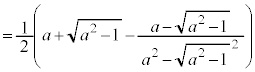
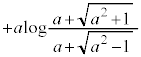
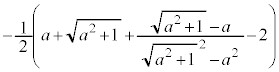
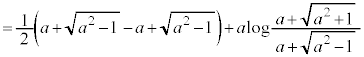
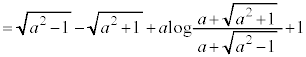 ......[��]
......[��]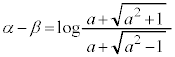
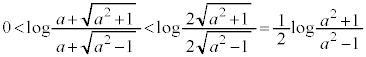
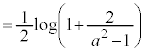
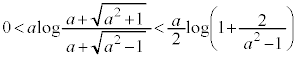
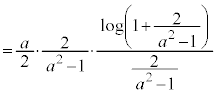
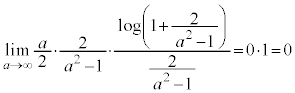
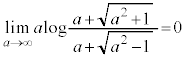 �@����A
�@����A