空間ベクトル
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
平面的な世界を2次元の世界、空間的な世界を3次元の世界と言いますが、この2とか3とか言うのは、平面ベクトル、空間ベクトルにおける1次独立なベクトルの個数です。平面座標では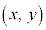
だったものが、空間座標では
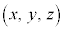になりますが、座標が1個増えて、ベクトルを成分表示したときの成分も1個増えます。ですが、これ以外では、平面ベクトルと、空間ベクトルの間で、基本的にベクトルとしての性質には違いはありません。
ここで学習する内容は、以下の通りです。各項目をクリックしてください。
空間座標 空間座標では、x座標，y座標のほかに、z座標が加わって、3個の座標で位置を指定します。 空間ベクトル 空間ベクトルと平面ベクトルとでほとんど違いがないのですが、ここでは、空間と平面とで共通の性質、異なる表現について整理します。 平面のベクトル方程式 空間図形で、平面をベクトルとして扱うときは、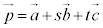
という形の方程式を用います。座標空間では、
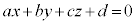という形の方程式を用います。共面条件：“同一平面上にない4点、O，A，B，Cに対して、
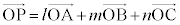となるPがA，B，Cと同一の平面上にある ⇔ 
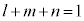” も扱います。 四面体の体積 四面体の体積を求める方法を学びます。外積の利用により容易に求める方法があります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
は球面を表します。
と点
との距離は、