���H�吔�w'22�N�O��[5]
a��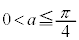 ���������Ƃ��A
���������Ƃ��A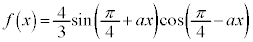 �Ƃ���B���̂Ƃ��A���̖₢�ɓ�����B
�Ƃ���B���̂Ƃ��A���̖₢�ɓ�����B
(1) ���̓���(��)����a������1���݂��邱�Ƃ������B
(��)�@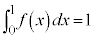
(2) 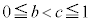 ��������b�Cc�ɂ��āA�s����
��������b�Cc�ɂ��āA�s���� �����藧���Ƃ������B
(3) ���̎��s���l����B
[���s]�@n�̐�1�C2�C����Cn���o�ڂƂ���C���郋�[���b�g��k��܂킷�B
����[���s]�ɂ����āA�e �ɂ���i���o����
�ɂ���i���o����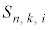 �Ƃ��A
�Ƃ��A (����)�@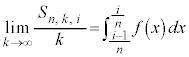
�����藧�Ƃ���B���̂Ƃ��A(1)�̓���(��)�����藧���Ƃ������B
(4) (3)��[���s]�ɂ����ďo�����̕��ϒl��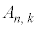 �Ƃ��A
�Ƃ��A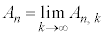 �Ƃ���B(����)�����藧�Ƃ��A�Ɍ�
�Ƃ���B(����)�����藧�Ƃ��A�Ɍ�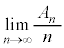 ��a��p���ĕ\���B
��a��p���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�O�������́A�m�����x���̂��Ƃ��낤�Ƒz��ł���Ǝv���܂����A�u�o�ځv���āH�㔼�͖�蕶���킩��ɂ����A������Ǝ��g�߂��������l�����̂��낤�Ǝv���Ă��܂��܂��B
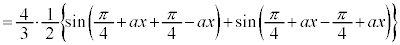
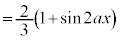 �@����@
�@����@������(��)�́A
�� 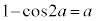 �@(
�@(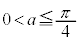 )
) 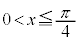 �ɂ����āA
�ɂ����āA �̃O���t���P�����������ɓʁB
�̃O���t���P�����������ɓʁB �̂Ƃ�
�̂Ƃ�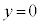 �C
�C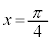 �̂Ƃ�
�̂Ƃ�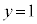
����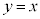 �́A
�́A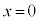 �̂Ƃ�
�̂Ƃ� �C
�C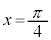 �̂Ƃ�
�̂Ƃ�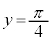 (
( )����āA
)����āA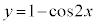 �̃O���t�ƒ���
�̃O���t�ƒ��� �́A
�́A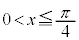 �ɂ����Ă���1�̌�_�������܂��B�܂�A(��)����a������1���݂��܂��B
�ɂ����Ă���1�̌�_�������܂��B�܂�A(��)����a������1���݂��܂��B
(2) 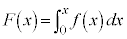 �Ƃ����ƁA
�Ƃ����ƁA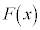 ��
�� �ɂ����ĘA���A
�ɂ����ĘA���A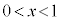 �ɂ����Ĕ����\�Ȃ̂ŁA���ϒl�̒藝�̐����v�������܂��B����āA���ϒl�̒藝���A
�ɂ����Ĕ����\�Ȃ̂ŁA���ϒl�̒藝�̐����v�������܂��B����āA���ϒl�̒藝���A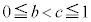 �ƂȂ�b�Cc�ɑ��āA
�ƂȂ�b�Cc�ɑ��āA 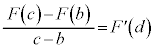 �C
�C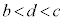 �@����A
�@����A��������d�����݂��܂��B
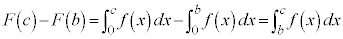 �@����B
�@����B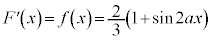 �C
�C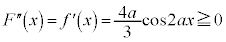
�A�C�B���A
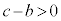 ���A
���A 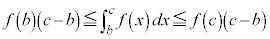 �@����C
�@����C
(3) ���[���b�g��k��܂킷�ԂɁA1�C2�C����Cn�̂����ꂩ���o�܂��Bi���o����(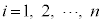 )��
)��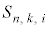 �Ƃ���̂ŁA1���o����
�Ƃ���̂ŁA1���o���� �C2���o����
�C2���o����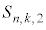 �C����Cn���o����
�C����Cn���o����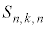 ���������킹���k�ɂȂ�܂��B�܂�A
���������킹���k�ɂȂ�܂��B�܂�A ������Ak�ɂ�炸��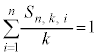 (���)�ƂȂ�̂ŁA
(���)�ƂȂ�̂ŁA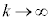 �̋Ɍ��ɂ����Ă��A
�̋Ɍ��ɂ����Ă��A 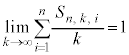 �@����D
�@����D(����)�̉E�ӂɂ��āA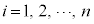 �ɂ��Ă̘a���Ƃ�ƁA
�ɂ��Ă̘a���Ƃ�ƁA 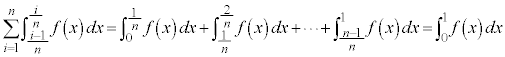 �@����E
�@����E����ŁA(����)���A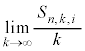 �͎������āA
�͎������āA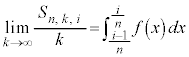 �Ȃ̂ł��̘a�ɂ��Ă��������āA�D���A
�Ȃ̂ł��̘a�ɂ��Ă��������āA�D���A ����āA�E���A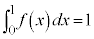 �ƂȂ�(��)�����藧���܂��B
�ƂȂ�(��)�����藧���܂��B
(4) (3)���i���o���m��(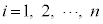 )��
)�� �ł��B�o���������ϒl�́A
�ł��B�o���������ϒl�́A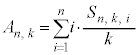 �C��L�̂悤��
�C��L�̂悤��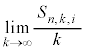 ����������̂ŁA�^�����A
����������̂ŁA�^�����A 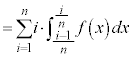 �@(�� (����))�@����F
�@(�� (����))�@����F�����Ŋe�ӂ�i�������āA �ɂ��Ă̘a���Ƃ�ƁA�F���A
�ɂ��Ă̘a���Ƃ�ƁA�F���A �Ɍ�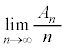 �����߂����̂ŁA�����n�Ŋ���A
�����߂����̂ŁA�����n�Ŋ���A 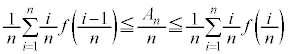 �@����G
�@����G�����ŁA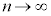 �Ƃ���ƁA�敪���ϖ@��p����ƁA�G�̍��ӂƉE�ӂ́A
�Ƃ���ƁA�敪���ϖ@��p����ƁA�G�̍��ӂƉE�ӂ́A �@���A
����āA�G�ɂ�����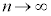 �Ƃ��āA
�Ƃ��āA ���ӁF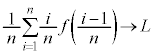
�E�ӁF
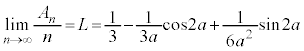 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 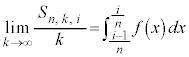
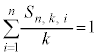 (���)�ƂȂ�̂ŁA
(���)�ƂȂ�̂ŁA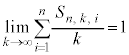 �@����D
�@����D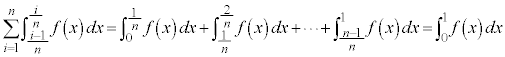 �@����E
�@����E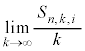 �͎������āA
�͎������āA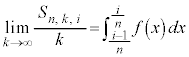 �Ȃ̂ł��̘a�ɂ��Ă��������āA�D���A
�Ȃ̂ł��̘a�ɂ��Ă��������āA�D���A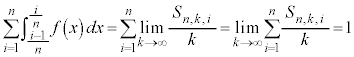
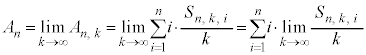
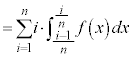 �@(�� (����))�@����F
�@(�� (����))�@����F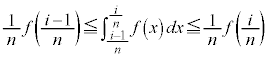
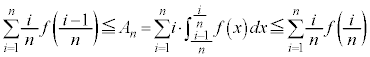
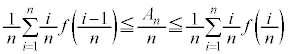 �@����G
�@����G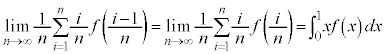
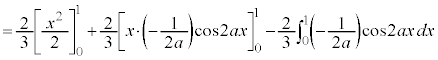
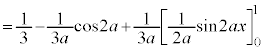
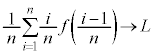

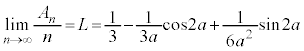 ......[��]
......[��]