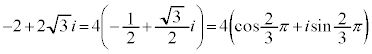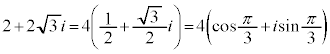���H�吔�w'23�N�O��[3]
�����������ꂽ3���̃J�[�h �C
�C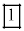 �C
�C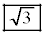 ����A����ׂ�2���̃J�[�h�����ɑI�сA�o�����������Ɏ����Ƌ����ɂ����f���鑀����l����B���̐���n�ɑ��āA���̑����n��J��Ԃ��ē�����n�̕��f���̐ς�
����A����ׂ�2���̃J�[�h�����ɑI�сA�o�����������Ɏ����Ƌ����ɂ����f���鑀����l����B���̐���n�ɑ��āA���̑����n��J��Ԃ��ē�����n�̕��f���̐ς�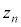 �ŕ\���B
�ŕ\���B
(1) 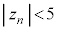 �ƂȂ�m��
�ƂȂ�m��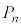 �����߂�B
�����߂�B (2) 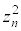 �������ƂȂ�m��
�������ƂȂ�m��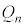 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(2)��n��̑���̊e��ɂł��镡�f����2�悪�S�������ł���悢�A�ƍ��o���Ղ��ł����A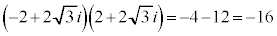 �Ƃ�����ɁA�����łȂ����f�����m�̐ς������ɂȂ�ꍇ���l������K�v������܂��B
�Ƃ�����ɁA�����łȂ����f�����m�̐ς������ɂȂ�ꍇ���l������K�v������܂��B
n��̑���̊e��ɂł������f����α�Ƃ��܂��B
�e��̑���̃J�[�h�̈������́A�ȉ��̂悤��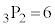 �ʂ肠��܂��B
�ʂ肠��܂��B
�E0�C1�ƈ����ƁA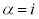 �ł��B
�ł��B
�E0�C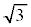 �ƈ����ƁA
�ƈ����ƁA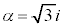 �ł��B
�ł��B
�E1�C0�ƈ����ƁA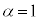 �ł��B
�ł��B
�E1�C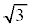 �ƈ����ƁA
�ƈ����ƁA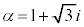 �ł��B
�ł��B
�E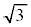 �C0�ƈ����ƁA
�C0�ƈ����ƁA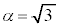 �ł��B
�ł��B
�E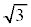 �C1�ƈ����ƁA
�C1�ƈ����ƁA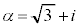 �ł��B
�ł��B
(1) 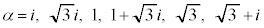 �̊e�X�ɂ��āA
�̊e�X�ɂ��āA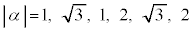 �ƂȂ�A�e���6�ʂ�̃J�[�h�̈������̂����A
�ƂȂ�A�e���6�ʂ�̃J�[�h�̈������̂����A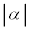 �́A1��2�ʂ�A
�́A1��2�ʂ�A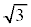 ��2�ʂ�A2��2�ʂ肠��܂��B
��2�ʂ�A2��2�ʂ肠��܂��B 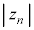 �͊e��ɂł������f���̐�Βl�̐ςł��B
�͊e��ɂł������f���̐�Βl�̐ςł��B
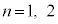 �̂Ƃ��A
�̂Ƃ��A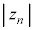 �͍��X4�ŁA�J�[�h�̈������ɂ�����炸
�͍��X4�ŁA�J�[�h�̈������ɂ�����炸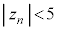 �ƂȂ�̂ŁA�m����
�ƂȂ�̂ŁA�m����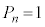
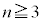 �̂Ƃ��A
�̂Ƃ��A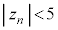 �ƂȂ�̂́A
�ƂȂ�̂́A(i) n��S�āA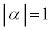 �ƂȂ�(�m��
�ƂȂ�(�m��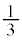 )�ꍇ���A
)�ꍇ���A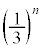
(ii) n��̂���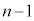 ��
��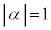 �ƂȂ�A1��
�ƂȂ�A1��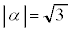 �܂���
�܂���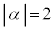 �ƂȂ�(�m��
�ƂȂ�(�m��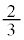 )�ꍇ���An��̂����ǂ�1��
)�ꍇ���An��̂����ǂ�1��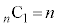 �ʂ肠��A
�ʂ肠��A (iii) n��̂���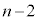 ��
��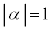 �ƂȂ�A2��A
�ƂȂ�A2��A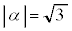 �܂���
�܂���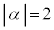 �A�ƂȂ�ꍇ���An��̂����ǂ�2��
�A�ƂȂ�ꍇ���An��̂����ǂ�2��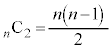 �ʂ肠��A
�ʂ肠��A ���߂�m���́A
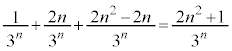 �@(
�@(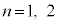 �̂Ƃ�������) .....[��]
�̂Ƃ�������) .....[��]
(2) 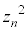 ���������ǂ�����������ɂ��Ă���̂ŁA
���������ǂ�����������ɂ��Ă���̂ŁA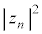 �͊m���ɂ͉e�����Ȃ����Ƃɒ��ӂ��܂��B
�͊m���ɂ͉e�����Ȃ����Ƃɒ��ӂ��܂��B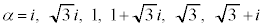 �̊e�X�ɂ��āA
�̊e�X�ɂ��āA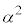 �́A
�́A �ƂȂ�܂��B6�ʂ��α�ɑ��āA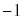 �C
�C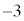 �C1�C3��4�ʂ��
�C1�C3��4�ʂ��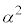 �������ł��B�c��2�ʂ��
�������ł��B�c��2�ʂ��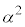 �ɂ��āA�Ɍ`���ŕ\���ƁA
�ɂ��āA�Ɍ`���ŕ\���ƁA 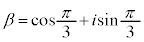 �Ƃ����ƁA
�Ƃ����ƁA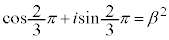 ���A
���A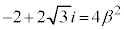 �C
�C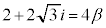
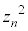 �͊e��̑���ł�
�͊e��̑���ł�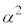 ���������킹�����̂ŁA
���������킹�����̂ŁA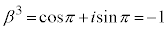 �C
�C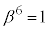 (1�̗ݏ捪���Q��)�ɒ��ӂ���ƁAm��0�ȏ�̐����Ƃ��āA
(1�̗ݏ捪���Q��)�ɒ��ӂ���ƁAm��0�ȏ�̐����Ƃ��āA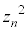 �̒��ŁAβ��
�̒��ŁAβ��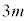 �����킳��Ă���A
�����킳��Ă���A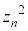 �͎����ɂȂ�܂��Bβ��
�͎����ɂȂ�܂��Bβ��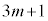 ��A���邢��
��A���邢��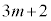 �����킳��Ă���ꍇ�́A
�����킳��Ă���ꍇ�́A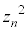 �͋����ɂȂ�܂��B
�͋����ɂȂ�܂��B
�����ŁAn���A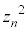 �̒��ŁAβ��
�̒��ŁAβ��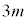 �����킳��Ă���m����
�����킳��Ă���m����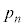 (
(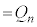 )�C�
)�Cβ��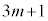 �����킳��Ă���m����
�����킳��Ă���m����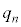 �Cβ��
�Cβ��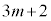 �����킳��Ă���m����
�����킳��Ă���m����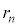 �Ƃ���ƁA
�Ƃ���ƁA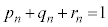 �@����@
�@����@�ł����āA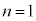 �̂Ƃ��A
�̂Ƃ��A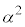 �������ł���̂�4�ʂ�A
�������ł���̂�4�ʂ�A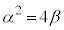 ��1�ʂ�A
��1�ʂ�A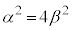 ��1�ʂ�ŁA
��1�ʂ�ŁA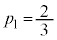 �C
�C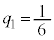 �C
�C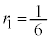 �@����A
�@����A
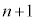 ��ڂŁA
��ڂŁA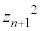 �̒���β��
�̒���β��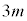 ��A���邢��
��A���邢��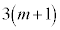 �����Ă���̂́A
�����Ă���̂́A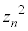 �̒���β��
�̒���β��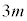 �����Ă���
�����Ă���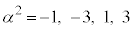 �̂����ꂩ��
�̂����ꂩ��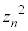 �ɂ�����Ƃ�(�m��
�ɂ�����Ƃ�(�m��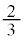 )�A���邢�́A
)�A���邢�́A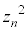 �̒���β��
�̒���β��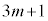 �����킳��Ă���
�����킳��Ă���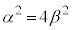 ��
��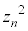 �ɂ�����Ƃ�(�m��
�ɂ�����Ƃ�(�m��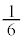 )�A���邢�́A
)�A���邢�́A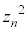 �̒���β��
�̒���β��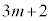 �����킳��Ă���
�����킳��Ă���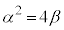 ��
��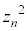 �ɂ�����Ƃ�(�m��
�ɂ�����Ƃ�(�m��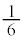 )�ŁA
)�ŁA �@���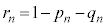 ��������ƁA
��������ƁA 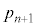 ��
��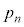 ��x�Ƃ����ƁA
��x�Ƃ����ƁA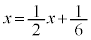 ����C
����C
�� 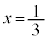
�B�|�C���A
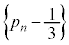 �́A�A��菉��
�́A�A��菉��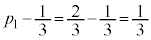 �C����
�C����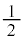 �����䐔���ł��B����āA
�����䐔���ł��B����āA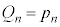 ���A
���A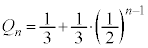 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
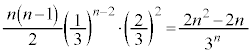
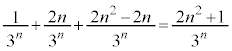 �@(
�@(