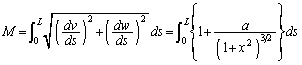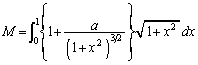���嗝�H���w'03�N[5]
������ �̂����A
�̂����A �̕�����C�Ƃ���BC��̓_P
�̕�����C�Ƃ���BC��̓_P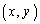 �ɑ��A���_O����P�܂ł�C�̕����̒�����s�ŕ\���Bx��y��s�̊��Ƃ݂Ȃ���
�ɑ��A���_O����P�܂ł�C�̕����̒�����s�ŕ\���Bx��y��s�̊��Ƃ݂Ȃ���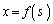 �C
�C �Ƃ����Ƃ��A�ȉ��̖₢�ɓ�����B
�Ƃ����Ƃ��A�ȉ��̖₢�ɓ�����B
(1) 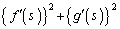 �̒l�����߂�B
�̒l�����߂�B (2) ���̓����������B
 �C
�C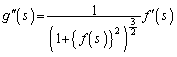
(3) P�ɂ�����C�̖@����ɂ���AP�Ƃ̋��������̒萔a�ł���2�_�̂����AC�̉����ɂ�����̂�Q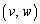 �Ƃ���Bv�Cw��
�Ƃ���Bv�Cw��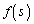 �C
�C �C
�C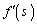 �C
�C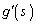 ��p���ĕ\���B
��p���ĕ\���B (4) C�̒�����L�Ƃ��AP��C�S�̂��Ƃ��́AQ�̕`���Ȑ��̒�����M�Ƃ���B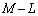 �����߂�B�������A
�����߂�B�������A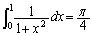 ��p���Ă��悢�B
��p���Ă��悢�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�Ȑ��̒����́A���s�w�K�w���v�͈̂̔͊O(�u��Ƃ苳��v�������ɂ�蕜�����邱�ƂɂȂ��Ă��܂�)�Ȃ̂ł����A�{��ł́A���ǍŌ�܂ŁA�Ȑ��̒����̐ϕ����v�Z���Ȃ��ł���ł��܂��̂ŁA�ȉ��ł́A�u�Ȑ��̒����v���A
�Ȑ� ��
�� �̕����̒����ł���A
�̕����̒����ł���A
�}��ϐ��\�����ꂽ�Ȑ� �C
�C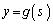 ��
��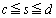 �̕����̒����ł���A
�̕����̒����ł���A
�Ƃ�����ϕ��ɓǂݑւ��Ă��������B
������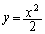 ��
�� �̕����̒���s�́A
�̕����̒���s�́A ���A
���A
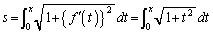 �@����@
�@����@
���D�@�̒�ϕ��̌v�Z�́A���嗝�n'02�N�O��[4]�A�u���ϕ�(����3)�̗�3���Q�Ƃ��Ă��������B�{��ł́A���ǍŌ�܂Ōv�Z���܂���B�������A���嗝�H'98�N[5]�ł́A�v�Z����K�v�̂����肪�o�肳��Ă��܂��B
 �@����B
�@����B�� 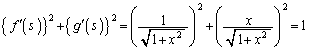 ......[��]
......[��]
(2)  �ł����A�A�ł�
�ł����A�A�ł� ��x�̎��ŕ\����Ă���̂ŁA�������̔����@�𗘗p���āA
��x�̎��ŕ\����Ă���̂ŁA�������̔����@�𗘗p���āA ���܂�x�Ŕ������A
���܂�x�Ŕ������A �������邱�Ƃɂ��܂��B
�������邱�Ƃɂ��܂��B 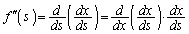 �@
�@
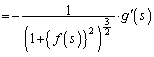 �@(�� �B)
�@(�� �B)���l�ɂ��āA
P�����_�̏ꍇ(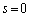 )�������āA�@���̌X���́A
)�������āA�@���̌X���́A �@(
�@(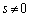 �C�܂�A
�C�܂�A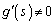 )�E�}�Œ��p�O�p�`PQR�ɂ��āAQR�FPQ =
)�E�}�Œ��p�O�p�`PQR�ɂ��āAQR�FPQ = 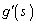 �F
�F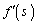 ��(1)�̌��ʂ��A
��(1)�̌��ʂ��A  �C
�C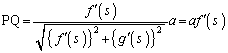
Q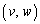 ��C�̉����ɗ���̂ŁA
��C�̉����ɗ���̂ŁA  �C
�C ......[��]
......[��]P�����_�̏ꍇ(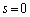 )��Q
)��Q �ł����A
�ł����A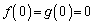 �C(1)�̌��ʂ��
�C(1)�̌��ʂ�� �̂Ƃ�
�̂Ƃ�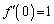 �Ȃ̂ŁA����
�Ȃ̂ŁA����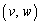 ��OK�ł��B
��OK�ł��B
(4) �Ȑ�C�̒���L�́A�@�̒�ϕ��̏�[��1�Ƃ��āA
 �@����C
�@����C(3)�̌��ʂ�Q�̕`���Ȑ��̔}��ϐ��\���ƌ��āA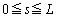 �̕����̋Ȑ��̒���M�́A
�̕����̋Ȑ��̒���M�́A  �@����D
�@����D(2)�C(3)�̌��ʂ�p���āA
 �@(�����ɒ���)
�@(�����ɒ���)�������A�D�̍������́A
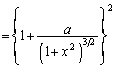 �@(�� (1))
�@(�� (1))����āA�D�́A
��ϕ�����x�̊��̌`�����Ă���̂ŁAs�Ɋւ���ϕ���x�Ɋւ���ϕ��Ƃ��邽�߂ɁA�@��p�����u���ϕ����܂��B ���A
���A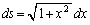 �Cs�F
�Cs�F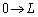 �̂Ƃ��Ax�F
�̂Ƃ��Ax�F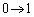
�� 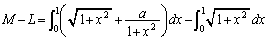
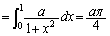 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  �C
�C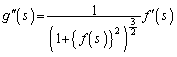
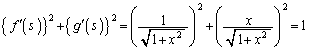 ......[��]
......[��]
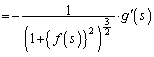 �@(�� �B)
�@(�� �B) �C
�C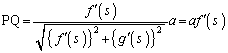
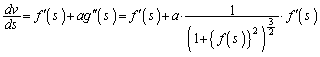
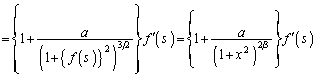
 �@(�����ɒ���)
�@(�����ɒ���)

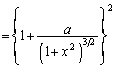 �@(�� (1))
�@(�� (1))