���Q�啨��'09�N[4]
 �}1(a)�̂悤�ɁA�f�M�ނ���Ȃ���a�f�ʐ�
�}1(a)�̂悤�ɁA�f�M�ނ���Ȃ���a�f�ʐ�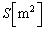 �̉~���^�V�����_�[�Ǝ���
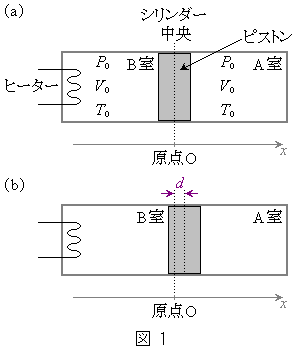
�̉~���^�V�����_�[�Ǝ���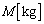 �̃s�X�g���������ɐݒu���Ă���B�s�X�g���̓V�����_�[�����~���ɓ����A�V�����_�[�Ƃ̊Ԃ̖��C�͖����ł���B�V�����_�[�̗��[�ɂ̓s�X�g���ɂ��u���ꂽ�C�����̍���2�̋��(A�������B��)�����݂��A���ꂼ��ɋC�̂��ł���B�܂��AB���ɂ͒ʓd���M�ɂ��q�[�^�[���ݒu���Ă���A�K�v�ɉ����ċC�̂����M�ł���B
�̃s�X�g���������ɐݒu���Ă���B�s�X�g���̓V�����_�[�����~���ɓ����A�V�����_�[�Ƃ̊Ԃ̖��C�͖����ł���B�V�����_�[�̗��[�ɂ̓s�X�g���ɂ��u���ꂽ�C�����̍���2�̋��(A�������B��)�����݂��A���ꂼ��ɋC�̂��ł���B�܂��AB���ɂ͒ʓd���M�ɂ��q�[�^�[���ݒu���Ă���A�K�v�ɉ����ċC�̂����M�ł���B
���܁A�P���q���q����Ȃ闝�z�C�̂𗼎���1���������������Ƃ��A�s�X�g���̓V�����_�[�̒����ł荇���A���̂Ƃ��̗����̈��́A�̐ρA���x�́A���ꂼ��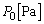 �C
�C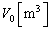 �C
�C �ł������B�V�����_�[�̒��������W���_O�Ƃ��āAA�����ւ̃s�X�g���̕ψ�
�ł������B�V�����_�[�̒��������W���_O�Ƃ��āAA�����ւ̃s�X�g���̕ψ�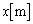 �𐳂Ƃ��A�s�X�g���̉^���͉t�I�ɂȂ������̂Ƃ��āA�ȉ��̖₢�ɓ�����B
�𐳂Ƃ��A�s�X�g���̉^���͉t�I�ɂȂ������̂Ƃ��āA�ȉ��̖₢�ɓ�����B
��1�@�O���ƔM�̂��Ƃ���s��Ȃ��C�̂̏�ԕω���f�M�ω��ƌĂԁB���̍ہA����P�Ƒ̐�V�̊Ԃɂ́A�C�̂̎�ނɈˑ�����w��b (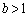 )��p���āA���̊W�����藧���Ƃ��m���Ă���B
)��p���āA���̊W�����藧���Ƃ��m���Ă���B ���܁A�}1(b)�̂悤�ɁA�s�X�g�������_O����A��������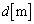 �����������ړ���������A�Â��ɉ������ƁA�s�X�g���͒P�U�����n�߂��B�s�X�g���̉^���ɂ��ďq�ׂ��ȉ��̕��͒��̋�K���Ȑ������邢�͎��Ŗ��߂�B�������A�ɗp���邱�Ƃ��ł��镶���́AS�CM�C
�����������ړ���������A�Â��ɉ������ƁA�s�X�g���͒P�U�����n�߂��B�s�X�g���̉^���ɂ��ďq�ׂ��ȉ��̕��͒��̋�K���Ȑ������邢�͎��Ŗ��߂�B�������A�ɗp���邱�Ƃ��ł��镶���́AS�CM�C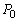 �C
�C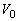 �Cb�Cx�Cd�ł���B
�Cb�Cx�Cd�ł���B
�s�X�g�����C�ӂ̕ψ� �̂Ƃ���A���̑̐ς�x��p���ĕ\���ƁA (1)
�̂Ƃ���A���̑̐ς�x��p���ĕ\���ƁA (1) 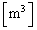 �ƂȂ�A���̂Ƃ���A���̈��͂� (2)
�ƂȂ�A���̂Ƃ���A���̈��͂� (2)  �ƕ\�����B��ʂɁA�ϐ�
�ƕ\�����B��ʂɁA�ϐ�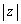 ��1�ɔ�ׂď\���������Ƃ��A
��1�ɔ�ׂď\���������Ƃ��A �̋ߎ��������藧�Ƃ����m���Ă���B���܁A������Ԃ���̑̐ϕω��ʂ�
�̋ߎ��������藧�Ƃ����m���Ă���B���܁A������Ԃ���̑̐ϕω��ʂ�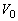 �ɔ�ׂď\�����������Ƃ��l������ƁA(2)�� (3)
�ɔ�ׂď\�����������Ƃ��l������ƁA(2)�� (3)  �̂悤�ɋߎ����邱�Ƃ��ł���B���̋ߎ��̂��ƂɁAB���̈��͂� (4)
�̂悤�ɋߎ����邱�Ƃ��ł���B���̋ߎ��̂��ƂɁAB���̈��͂� (4)  �ƂȂ�B�����2�̈��͂�p���A�s�X�g���̉����x��
�ƂȂ�B�����2�̈��͂�p���A�s�X�g���̉����x��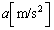 �Ƃ��ĉ^���������𗧂Ă�ƁA
�Ƃ��ĉ^���������𗧂Ă�ƁA (5) �ƂȂ�B����ꂽ�^������������A�s�X�g�����p�U���� (6)
(5) �ƂȂ�B����ꂽ�^������������A�s�X�g�����p�U���� (6)  �̒P�U�����s���A����
�̒P�U�����s���A����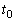 �� (7)
�� (7) 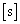 �ł��邱�Ƃ��킩��B�܂��A�s�X�g���́Ax�� (8)
�ł��邱�Ƃ��킩��B�܂��A�s�X�g���́Ax�� (8) 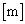 �̂Ƃ��ɍő�̑��� (9)
�̂Ƃ��ɍő�̑��� (9)  �ɂȂ�B
�ɂȂ�B
��2�@���ɁA�s�X�g����A�����֑傫���ړ������AA���̑̐ς� �ɂ����B
�ɂ����B (1) �s�X�g�����ړ��������A�������B���̈��͂���щ��x�����߂�B
�ĂсA�s�X�g�������_O�ŐÎ~������Ԃɖ߂��AB���ɐݒu����Ă���q�[�^�[�ɒʓd���邱�Ƃɂ��AB�����̋C�̂���l�ɉ��M�����B���M�̐i�s�ɔ����s�X�g���͂�������A�����ֈړ����AA���̑̐ς����傤��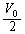 �ɂȂ������_�ʼn��M���~�߂��B
�ɂȂ������_�ʼn��M���~�߂��B (2) ���M���A�������B���̈��͂���щ��x�����߂�B
(3) �q�[�^�[����B���ɓ������ꂽ�M�ʁA�Ȃ�тɃs�X�g����ʂ���B���̋C�̂������d�������߂�B�������A�K�v�ł���C�̂̔M�e�� ��p����B
��p����B
��3�@A�����͒P���q���q�̗��z�C�̂̂܂܁AB������1�����̓q���q����Ȃ闝�z�C�̂ɒu���������BB�����̋C�̂�u���������ق��́A��1�Ƃ��ׂē��������̂��ƂŔ����U���������B���̖₢�ɓ�����B�Ȃ��A�P���q���q����ѓq���q����Ȃ闝�z�C�̂̎w��b�́A���ꂼ��A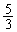 �C
�C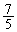 �ł���B
�ł���B  (1) A�������B���̈��͂Ƒ̐ς̊W��\�����}2�̃O���t�̒�����A�ł��K���Ȃ��̂�1�I�ׁB
(1) A�������B���̈��͂Ƒ̐ς̊W��\�����}2�̃O���t�̒�����A�ł��K���Ȃ��̂�1�I�ׁB
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��C�o�l�ɂ���P�U���̖��ł��B
��1�@A���AB���̋C�̂͊O�����M�̂��Ƃ�����Ȃ��̂ŁA�P�U�����Ă���Ԃ̋C�̂̕ω����f�M�ω��ł��B (1) �s�X�g����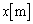 ����������(A��)�Ɉړ�����ƁAA�����̐��́A
����������(A��)�Ɉړ�����ƁAA�����̐��́A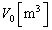 ����
����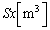 �������āA
�������āA �ƂȂ�܂��B
�ƂȂ�܂��B 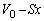 ......[��]
......[��](2) ���̂Ƃ���A����������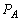 �Ƃ��āAA�����������̐��́A
�Ƃ��āAA�����������̐��́A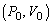 ��
��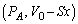 �ƕω�����̂ŁA��蕶�̊W��(�|�A�b�\���̊W��)�F
�ƕω�����̂ŁA��蕶�̊W��(�|�A�b�\���̊W��)�F (b�͔�M��ł�)���A
(b�͔�M��ł�)���A 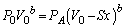 �@����@
�@����@�� 
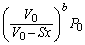 ......[��]
......[��] (3) 
������Ԃ�����̐ϕω����� �ɔ�ׂď\���������̂ŁA
�ɔ�ׂď\���������̂ŁA ���A
���A 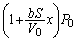 ......[��]
......[��](4) ���̂Ƃ���B����������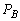 �Ƃ��āAB�����������̐��́A
�Ƃ��āAB�����������̐��́A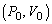 ��
��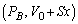 �ƕω�����̂ŁA�@���̉E�ӂ̃}�C�i�X���v���X�ɕς��������������A
�ƕω�����̂ŁA�@���̉E�ӂ̃}�C�i�X���v���X�ɕς��������������A �ł́A(3)�̌��ʂ�
�ł́A(3)�̌��ʂ�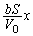 �̑O�̃v���X���}�C�i�X�ɕς��A
�̑O�̃v���X���}�C�i�X�ɕς��A  ......[��]
......[��](3)�C(4)�̌��ʂ�p���āA
 �@����A
�@����A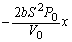 ......[��]
......[��](6) �A���A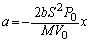
����́A�p�U����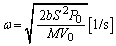 ���P�U����\���܂��B
���P�U����\���܂��B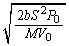 ......[��]
......[��] (7) ����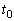 �́A
�́A 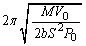 ......[��]
......[��](8) �A���́A�P�U�����U�����S��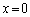 �ł��邱�Ƃ��Ӗ����A
�ł��邱�Ƃ��Ӗ����A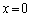 �ɂ����ăs�X�g���͍ő�������ɂȂ�܂��B
�ɂ����ăs�X�g���͍ő�������ɂȂ�܂��B 0 ......[��]
(9) �U�����S��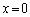 �ł����āA�ŏ���
�ł����āA�ŏ��� �Ńs�X�g����Â��ɗ������Ƃ��납��A�P�U�����U����d�ł��B�ő������
�Ńs�X�g����Â��ɗ������Ƃ��납��A�P�U�����U����d�ł��B�ő������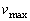 �́A�P�U���̌������A
�́A�P�U���̌������A 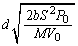 ......[��]
......[��]
��2(1) A���AB���̍ŏ��̏�Ԃł���ԕ������F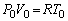 �@����B�@(
�@����B�@(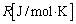 �͋C�̒萔)
�͋C�̒萔) �s�X�g���ړ����A���CB����������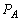 �C
�C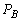 �C��Ή��x��
�C��Ή��x��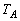 �C
�C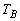 �Ƃ��܂��B�s�X�g���ړ���ɂ��āAA������ԕ������F
�Ƃ��܂��B�s�X�g���ړ���ɂ��āAA������ԕ������F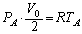 �@����CB������ԕ������F
�@����CB������ԕ������F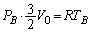 �@����D
�@����D
�C���B���A �@����E
�@����E
�D���B���A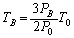 �@����F�O����������(�܂�A�s�X�g���ɂ��������ɂ��āA�荇���͐������Ă��Ȃ�)�u�s�X�g����A�����֑傫���ړ������v�Ƃ�����蕶�̋L�q����A���̊Ԃ̕ω����f�M�ω��ƍl�����܂��B�f�M�ω��̊W���F
�@����F�O����������(�܂�A�s�X�g���ɂ��������ɂ��āA�荇���͐������Ă��Ȃ�)�u�s�X�g����A�����֑傫���ړ������v�Ƃ�����蕶�̋L�q����A���̊Ԃ̕ω����f�M�ω��ƍl�����܂��B�f�M�ω��̊W���F ���A
���A  �C
�C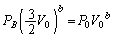
�� 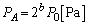 �C
�C ......[��]�E�C�F���A
......[��]�E�C�F���A 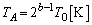 �C
�C ......[��]
......[��](2) ���M���A���CB����������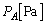 �C
�C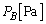 �C��Ή��x��
�C��Ή��x��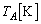 �C
�C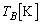 �Ƃ��܂��B�C�A�D�͂��̂܂ܐ������A�E�C�F�������ł��B�܂��AA���ɂ��ẮA�f�M�ω��̂܂�(B�����M��������̂Œf�M�ω��ł͂���܂���)�Ȃ̂ŁA
�Ƃ��܂��B�C�A�D�͂��̂܂ܐ������A�E�C�F�������ł��B�܂��AA���ɂ��ẮA�f�M�ω��̂܂�(B�����M��������̂Œf�M�ω��ł͂���܂���)�Ȃ̂ŁA 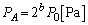 �C
�C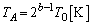 ......[��]
......[��]�ł����A���x�́A�s�X�g�����O����������킯�ł͂Ȃ��̂ŁA�s�X�g���ɓ����͂̂荇�����������A �� 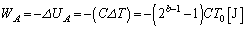
B���̋C�̂������d��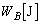 �́A
�́A 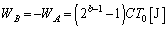 ......[��]
......[��]B���������G�l���M�[�̕ω�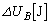 �́A
�́A �M�͊w��1�@�����A�q�[�^�[����
B���ɓ������ꂽ�M�� �́A
�́A 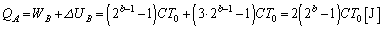 �@ ......[��]
�@ ......[��]���D�M�e��C�̒P��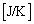 �ɒ��ӂ��Ă��������B��σ�����M
�ɒ��ӂ��Ă��������B��σ�����M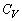 �̒P�ʂ�
�̒P�ʂ� �ŁAn�����̋C�̂������G�l���M�[��
�ŁAn�����̋C�̂������G�l���M�[��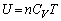 �ł��B�����ł́A
�ł��B�����ł́A �ł���AA���AB���̋C�̂�1�����Ȃ̂�
�ł���AA���AB���̋C�̂�1�����Ȃ̂� �ł���A
�ł���A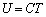 �C
�C �Ƃ��čl���܂��B
�Ƃ��čl���܂��B
�������A�P���q���q���z�C�̂Ȃ̂ŁA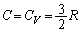 �Ƃ��Ă�OK�ł����A����C�̎g�p�ɂ��ẮA��3�̖�蕶���Ŕ�M��̒l���w�肵�Ă���̂ŁA
�Ƃ��Ă�OK�ł����A����C�̎g�p�ɂ��ẮA��3�̖�蕶���Ŕ�M��̒l���w�肵�Ă���̂ŁA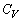 �̒l�𖢒m���Ƃ��Ă��ł���悤�ɁA�o��҂��z���������̂Ǝv���܂��B
�̒l�𖢒m���Ƃ��Ă��ł���悤�ɁA�o��҂��z���������̂Ǝv���܂��B
��3�@��1�Ɠ��������Ȃ̂ŁA�����U�����Ă���ԁAA���CB���Ƃ��A�C�̂͒f�M�ω����܂��BA����P���q���q�AB����q���q�Ƃ���̂ŁA�A����b���AA���ɂ��Ă� �CB���ɂ��Ă�
�CB���ɂ��Ă� �ɂ���K�v������A�A�́A
�ɂ���K�v������A�A�́A 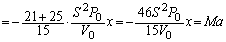 �@����G
�@����G�p�U������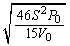 �C������
�C������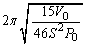 �@����HA���AB���Ƃ��ɒP���q���q���z�C�̂ł���A�A��
�@����HA���AB���Ƃ��ɒP���q���q���z�C�̂ł���A�A��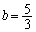 �Ƃ��A
�Ƃ��A �p�U������ �C������
�C������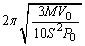 �@����I
�@����I (1) A���AB�����ꂼ��ɂ��āA������P�C�̐���V�Ƃ��āA�f�M�ω��̊W���F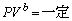 ���A
���A A���F �@����JB���F
�@����JB���F �@����K
�@����K �J�C�K�Ƃ��A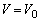 �̂Ƃ�
�̂Ƃ�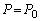 �ł����A
�ł����A
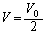 �̂Ƃ��AA���ł�
�̂Ƃ��AA���ł� �CB���ł�
�CB���ł� �C
�C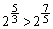 ���AA���̕����������傫���Ȃ�܂��B
���AA���̕����������傫���Ȃ�܂��B
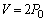 �̂Ƃ��AA���ł�
�̂Ƃ��AA���ł� �CB���ł�
�CB���ł� �C
�C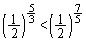 ���AB���̕����������傫���Ȃ�܂��B
���AB���̕����������傫���Ȃ�܂��B
�����Ȃ��Ă���O���t�́A(�E) ......[��] (2) �H�C�I������ƁA ���A�H�������̕����I�����������������Ƃ��킩��܂��B�܂��A�G���A�Е���q���q�ɕς��Ă��A�U�����S��
���A�H�������̕����I�����������������Ƃ��킩��܂��B�܂��A�G���A�Е���q���q�ɕς��Ă��A�U�����S��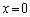 �̂܂ܕς��܂���B�����Ȃ��Ă���O���t�́A(�A) ......[��]
�̂܂ܕς��܂���B�����Ȃ��Ă���O���t�́A(�A) ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B