���H�啨��'06�N�O��[2]
�\���Ȓ������������ȉ~����V�����_�[���ɁA�Ȃ߂炩�ɓ����f�ʐ�A[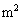 ]�̃s�X�g��������A�����ɒP���q���q�̗��z�C�̂������߂��Ă���B�V�����_�[�͉��x�����߂ł���悤�M���ɐڐG���Ă���B�܂��A�s�X�g���ɂ́A�V�����_�[�̒��S�����ʂ�d���̖����ł��鎅�ŁA���Ԃ�p���Ă�������艺���邱�Ƃ��ł���B���͂̈��͂�
]�̃s�X�g��������A�����ɒP���q���q�̗��z�C�̂������߂��Ă���B�V�����_�[�͉��x�����߂ł���悤�M���ɐڐG���Ă���B�܂��A�s�X�g���ɂ́A�V�����_�[�̒��S�����ʂ�d���̖����ł��鎅�ŁA���Ԃ�p���Ă�������艺���邱�Ƃ��ł���B���͂̈��͂�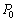 [Pa]�C�d�͉����x��g[
[Pa]�C�d�͉����x��g[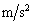 ]�Ƃ���B
]�Ƃ���B
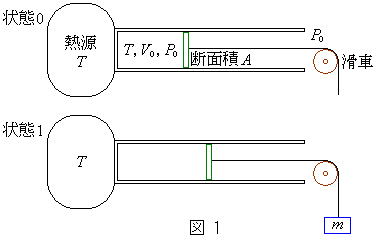 [A]�@�}1�̂悤�ɁA�M���̉��x��T[K]�C��������邵�Ă��Ȃ���Ԃł́A�C�̂̉��x��T[K}�C�̐ς�
[A]�@�}1�̂悤�ɁA�M���̉��x��T[K]�C��������邵�Ă��Ȃ���Ԃł́A�C�̂̉��x��T[K}�C�̐ς�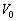 [
[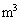 ]�C���͎͂��͂̈��͂Ɠ�����
]�C���͎͂��͂̈��͂Ɠ�����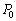 [Pa]�ł���A��������0�Ƃ���B�����̋C�̂̉��x���ω����Ȃ��悤�ɂ������Ƃ�����m[kg]���邷�ƁA�s�X�g���͂���ʒu�ŐÎ~�����1�ƂȂ����B���ɂ�������邵���܂܁A�M���̉��x���\�����Ԃ�������
[Pa]�ł���A��������0�Ƃ���B�����̋C�̂̉��x���ω����Ȃ��悤�ɂ������Ƃ�����m[kg]���邷�ƁA�s�X�g���͂���ʒu�ŐÎ~�����1�ƂȂ����B���ɂ�������邵���܂܁A�M���̉��x���\�����Ԃ�������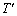 [K]�֏㏸�����ď��2�Ƃ����B
[K]�֏㏸�����ď��2�Ƃ����B(a) ���1�ɂ�����C�̂̈���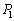 [Pa]�Ə��2�ɂ�����C�̂̑̐�
[Pa]�Ə��2�ɂ�����C�̂̑̐�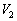 [
[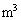 ]�����߂�B�܂��A���1�C���2�����̈���P-�̐�V�O���t�ɂ��ꂼ��_
]�����߂�B�܂��A���1�C���2�����̈���P-�̐�V�O���t�ɂ��ꂼ��_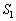 �C
�C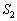 �Ƃ��Ď����A���0�Ə��1�̈��͍����L������B�������A���̓_
�Ƃ��Ď����A���0�Ə��1�̈��͍����L������B�������A���̓_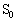 �͏��0���A�j����T�����
�͏��0���A�j����T�����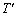 �̓������������Ă���B
�̓������������Ă���B (b) ���1������2�ւ̉ߒ��ŋC�̂��O���ɂ����d��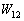 [J]�C����єM������V�����_�[���̋C�̂֓������M��
[J]�C����єM������V�����_�[���̋C�̂֓������M��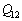 [J]�����߂�B
[J]�����߂�B [B]�@�M���̉��x��T�ɂ��A��������͂����ċC�̂����0�ɖ߂����B
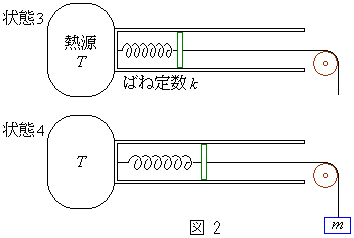 [C]�@�}2�悤�ɁA�V�����_�[�ƃs�X�g����̐ς̖����ł���˒萔k[
[C]�@�}2�悤�ɁA�V�����_�[�ƃs�X�g����̐ς̖����ł���˒萔k[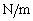 ]�̂˂ŘA�����A�M���̉��x��T�ɂ����B��������邵�Ă��Ȃ���Ԃł́A�C�̂̉��x�A���́A�̐ς͏��0�Ɠ����ł���A��������3�Ƃ���B��������A�����̋C�̂̉��x���ω����Ȃ��悤�ɂ������Ƃ�����m���邵�ď��4�Ƃ��A���ɁA�M���̉��x���\�����Ԃ�������
]�̂˂ŘA�����A�M���̉��x��T�ɂ����B��������邵�Ă��Ȃ���Ԃł́A�C�̂̉��x�A���́A�̐ς͏��0�Ɠ����ł���A��������3�Ƃ���B��������A�����̋C�̂̉��x���ω����Ȃ��悤�ɂ������Ƃ�����m���邵�ď��4�Ƃ��A���ɁA�M���̉��x���\�����Ԃ�������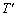 �֏㏸�����ď��5�Ƃ����B
�֏㏸�����ď��5�Ƃ����B(d) ���3������4�ւ̑̐ϕω���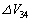 [
[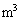 ]�Ƃ��āA���4�ɂ�����C�̂̈���
]�Ƃ��āA���4�ɂ�����C�̂̈���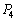 [Pa]�����߂�B
[Pa]�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@[B](c)�ŁA�͂̂肠�������ꂽ�Ƃ��ɁA�V�����_�[���̋C�̂��������s�X�g���ɂ��������ɉ����Ȃ��ėǂ��̂��A�f�M�ω��ōl����ׂ��Ȃ̂ł͂Ȃ����A�ǂ����A�������藈�Ȃ��̂ł����A��蕶�̏��������炵�āA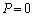 �ƍl���邵���Ȃ������ł��B
�ƍl���邵���Ȃ������ł��B
�V�����_�[���̋C�̗̂ʂ�n[mol]�C�C�̒萔��R[ ]�Ƃ��܂��B
]�Ƃ��܂��B
[A](a) ���1�ɂ����ăs�X�g���ɂ́A�V�����_�[���̋C�̂������ɂ��E��������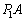 �C��C���ɂ�鍶��������
�C��C���ɂ�鍶��������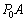 �C�E�����Ɏ���ʂ��Ă�����ɓ����d��
�C�E�����Ɏ���ʂ��Ă�����ɓ����d��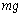 ���������Ă��܂��B�������͂̂荇�����A
���������Ă��܂��B�������͂̂荇�����A �� 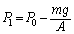 [Pa] ......[��]���0�ɂ�������ԕ������́A
[Pa] ......[��]���0�ɂ�������ԕ������́A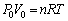 �@����@
�@����@
���1�ɂ�������ԕ������́A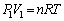 �@����A
�@����A
���1������2�܂ł̉ߒ��́A�s�X�g���ɓ����͂̂肠�������������܂܂̕ω��Ȃ̂ŁA�舳�ω��ł��B����āA���2�ɂ�����������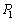 �ł��B
�ł��B
���2�ɂ�������ԕ������́A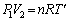 �@����B
�@����B
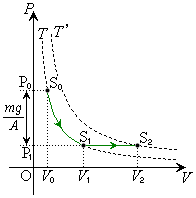 �@�C�A���(�܂����{�C���̖@�����)�A
�@�C�A���(�܂����{�C���̖@�����)�A �� 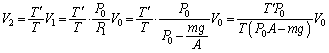 [
[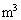 ] ......[��]
] ......[��]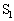 �C
�C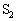 ����сA���0�Ə��1�����͍��A
����сA���0�Ə��1�����͍��A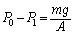 �́A�E�}�̒ʂ�B
�́A�E�}�̒ʂ�B
(b) ���1������2�ւ̉ߒ����C�̂��O���ɂ����d��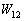 �́A
�́A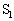 �C
�C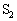 ������P-V�O���t��V���ŋ��܂ꂽ�����̖ʐςɂȂ�܂��B�@�C�A�C�B���A
������P-V�O���t��V���ŋ��܂ꂽ�����̖ʐςɂȂ�܂��B�@�C�A�C�B���A 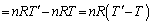
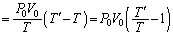 [J] ......[��]
[J] ......[��]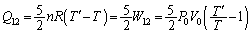 [J] ......[��]
[J] ......[��]
[B](c) �V�����_�[���̋C�̂�������P�Ƃ��܂��B�s�X�g���ɓ����͂̂荇�����A
�� 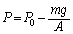 �@����C
�@����C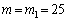 [kg]�̂Ƃ��ɂ́A�͂̂荇���C���������Ă��܂������A
[kg]�̂Ƃ��ɂ́A�͂̂荇���C���������Ă��܂������A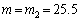 [kg]�̂Ƃ��ɂ́A�͂̂荇�����������Ȃ��Ƃ������Ƃ́A
[kg]�̂Ƃ��ɂ́A�͂̂荇�����������Ȃ��Ƃ������Ƃ́A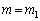 �̂Ƃ��ɂ́A�V�����_�[���̋C�̂��s�X�g�����������y�ڂ��āA
�̂Ƃ��ɂ́A�V�����_�[���̋C�̂��s�X�g�����������y�ڂ��āA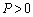 �������̂ɁA
�������̂ɁA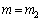 �̂Ƃ��ɂ́A�s�X�g�����E�ɓ����o�������߂ɁA�V�����_�[���̋C�̂��s�X�g���������y�ڂ����Ƃ��ł��Ȃ��Ȃ�A�s�X�g���ɓ��������������E�����A�܂�A
�̂Ƃ��ɂ́A�s�X�g�����E�ɓ����o�������߂ɁA�V�����_�[���̋C�̂��s�X�g���������y�ڂ����Ƃ��ł��Ȃ��Ȃ�A�s�X�g���ɓ��������������E�����A�܂�A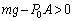 �ƂȂ����A�Ƃ������Ƃł��B
�ƂȂ����A�Ƃ������Ƃł��B
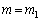 �̂Ƃ��A
�̂Ƃ��A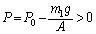 ���A
���A 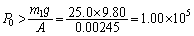 [Pa]
[Pa]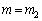 �̂Ƃ��A
�̂Ƃ��A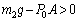 ���A
���A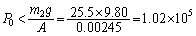 [Pa]
[Pa]�ȏ���A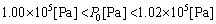 ......[��]
......[��]
[C](d) ���4�ɂ����āA�s�X�g���ɓ������́A�V�����_�[���̋C�̂������ɂ��E��������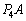 �C��C���ɂ�鍶��������
�C��C���ɂ�鍶��������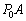 �C�˂��L����
�C�˂��L����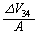 �ŁA�˂��������Ɉ�����
�ŁA�˂��������Ɉ�����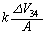 �C�E�����Ɏ���ʂ��Ă�����ɓ����d��
�C�E�����Ɏ���ʂ��Ă�����ɓ����d��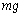 ���������Ă��܂��B�������͂̂荇�����A
���������Ă��܂��B�������͂̂荇�����A �� 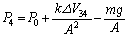 [Pa] ......[��]
[Pa] ......[��] ���4�����5�Ɏ���ߒ��ɂ����āA�̐���V�C������P�Ƃ���ƁA�˂��L����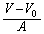 �ƂȂ�A�s�X�g���ɓ����͂̂荇���̎��́A
�ƂȂ�A�s�X�g���ɓ����͂̂荇���̎��́A �� 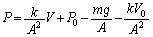 �@����D
�@����D
������A���4������5�Ɏ���ߒ���P-V�O���t�͒����ŁAV�̌W��������ƁA
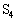 �C
�C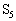 ��ʂ钼���̌X���́A
��ʂ钼���̌X���́A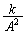 [
[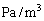 ] ......[��]
] ......[��]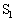 �C
�C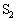 ��ʂ钼����ł́A������
��ʂ钼����ł́A������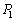 �ň��Ȃ̂ŁA�D�ɂ����āA
�ň��Ȃ̂ŁA�D�ɂ����āA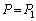 �Ƃ��āA
�Ƃ��āA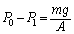 ���A
���A �� ��_���̐��́A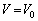 [
[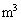 ] ......[��]
] ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  [
[