ÈwåHwn¨'25NOú[2]
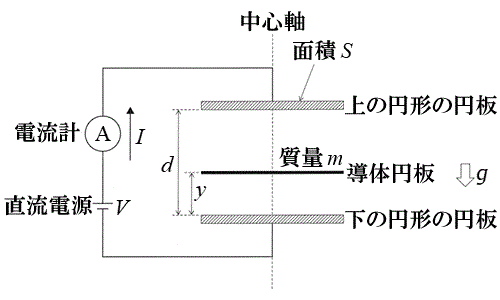 }Ìæ¤ÉA^óÉÊÏSÌ2Ì~`ÌÉÂðAS²ðí¹Ä
½ÉÅèµAãºÌÉÂÔÉNdÍV̼¬d¹Æd¬vðÂÈ®BÉAÉÂƯ¶ÊÏÅ¿Êm̱Ì~ÂðAÉÂÔÉS²ðí¹Ä}ü·éB±Ì~ÂÍÉÂÔð¼ûüÉڮūéªA»ÌÛAÉÂƽsðÛ¿A©Â
½ûüɸêé±ÆÈ®àÌÆ·éBܽA±Ì~ÂÌú³ÍÉÂÔÌ£dÆä×Ä\ª¬³¢Æ·éBÉÂ[â±Ì~Â[ɨ¯édêÌêͳūéBÉÂA±Ì~ÂA±üÌïRA¨æÑd¹Æd¬vÌàïRͳūéBÉÂƱÌ~ÂÌÚGɨ¯éd×Ìڮͬâ©ÉN±éàÌÆ·éB^óÌUd¦ð
}Ìæ¤ÉA^óÉÊÏSÌ2Ì~`ÌÉÂðAS²ðí¹Ä
½ÉÅèµAãºÌÉÂÔÉNdÍV̼¬d¹Æd¬vðÂÈ®BÉAÉÂƯ¶ÊÏÅ¿Êm̱Ì~ÂðAÉÂÔÉS²ðí¹Ä}ü·éB±Ì~ÂÍÉÂÔð¼ûüÉڮūéªA»ÌÛAÉÂƽsðÛ¿A©Â
½ûüɸêé±ÆÈ®àÌÆ·éBܽA±Ì~ÂÌú³ÍÉÂÔÌ£dÆä×Ä\ª¬³¢Æ·éBÉÂ[â±Ì~Â[ɨ¯édêÌêͳūéBÉÂA±Ì~ÂA±üÌïRA¨æÑd¹Æd¬vÌàïRͳūéBÉÂƱÌ~ÂÌÚGɨ¯éd×Ìڮͬâ©ÉN±éàÌÆ·éB^óÌUd¦ð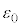 CdÍÁ¬xÌ嫳ð
CdÍÁ¬xÌ嫳ð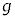 Æ·éB
Æ·éB
[A]@±Ì~ÂðºÌÉÂÆÚG³¹A»ÁÆèðÍÈ·B¼¬d¹ÌNdÍVª élæèàá¯êÎA±Ì~ÂÍ®©È¢B±ÌÆ«AȺÌÝâɦæB
(a) ±Ì~ÂÌãÊɶ¶éd×ðßæB
(b) ãÌÉÂƱÌ~ÂÅ\¬³êé½sÂRfT[É~¦çê½ÃdGlM[ðßæB
[B]@±Ì~ÂðºÌÉÂÆÚG³¹A»ÁÆèðÍÈ·B¼¬d¹ÌNdÍVª élæèà¯êÎA±Ì~ÂÍãðnßéBºÌÉÂÌ\Ê©ç±Ì~ÂÜÅÌ£ðyÆ·éB±ÌÆ«AȺÌÝâɦæB
ͶßÉAãɨ¯é±Ì~ÂÌ^®ðl¦éB
(c) ±Ì~ÂÌãÊƺÊɶ¶éd×ð»ê¼ê£yÌÖƵÄßæB
(d) ãºÌÉÂƱÌ~ÂÅ\¬³êé½sÂRfT[É~¦çê½SÃdGlM[ð£yÌÖƵÄßæB
(e) ±Ì~ÂÌ㸬xð£yÌÖƵÄßæB
(f) d¬vð¬êéd¬Ið£yÌÖƵÄßæBȨAd¬IÍ}ÌîóÌü«ð³Æ·éB
»ÌãA±Ì~ÂÍãÌÉÂÉÚG·éBãÌÉÂÉÚGµ½ ÆàÜßıÌ~ÂÌ^®ðl¦éB±Ì~ÂÆÉÂÆÌÚGÍ®Sñe«ÕËƼè·éB
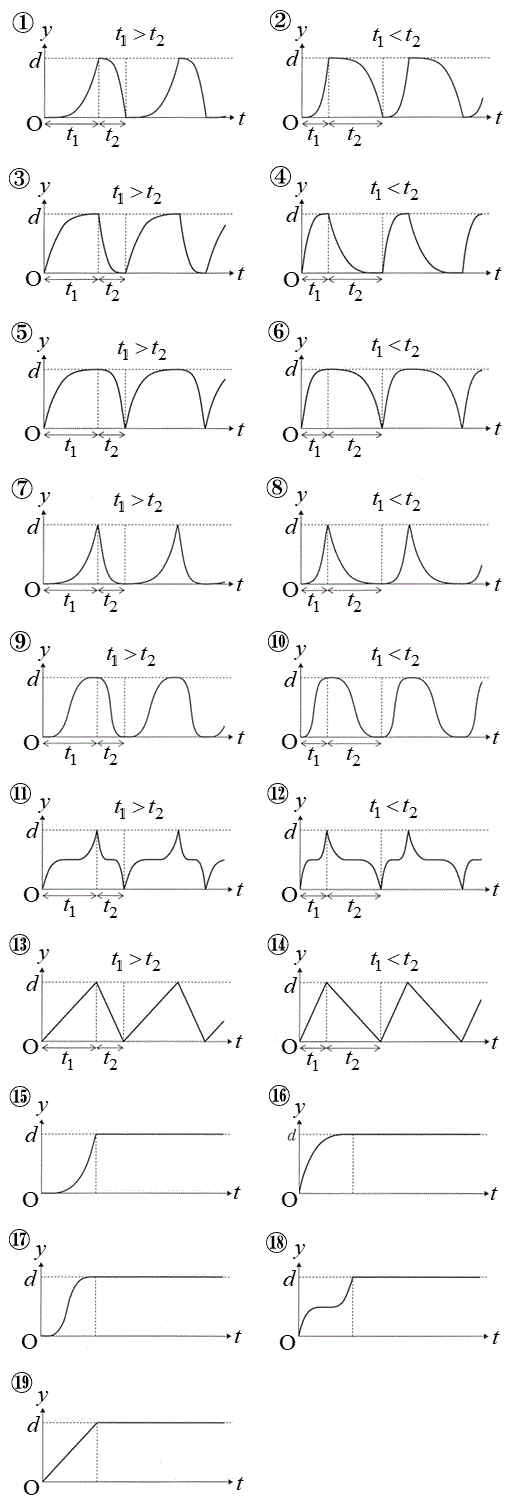 (g) ±Ì~ªãµnßéð
(g) ±Ì~ªãµnßéð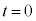 Ƶ½Æ«ÉAt Æ£yÌÖWƵÄÅàÓ³íµ¢àÌðAEÌ@`R©çI×BȨA
Ƶ½Æ«ÉAt Æ£yÌÖWƵÄÅàÓ³íµ¢àÌðAEÌ@`R©çI×BȨA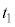 Æ
Æ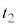 Íe}Åè`³êéÔÅ éB
Íe}Åè`³êéÔÅ éB
yLz±±©çLÅ·B²ÌF³Ü̲x²ððè½Aæ뵨袢½µÜ·B
yLzLͱ±ÜÅÅ·B
ð@{âà[1]ƯlÉîbÉÖ·éâèÅ·ªAîb¾©çƾÁÄÕµ¢Æ¢¤í¯ÅÍ èܹñBJÈl@ªKvÅ·B
[A](a) ÉÂÔuªdÌÆ«A±Ì~ÂãÆãÌ~`~ÂÌÔÉÅ«éRfT[ÌÃdeÊÍ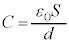 C±êÉd³Vð©¯éÆ«RfT[ɶ¶éd×QÍA
C±êÉd³Vð©¯éÆ«RfT[ɶ¶éd×QÍA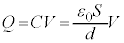 C±Ì~ÂÌãÊɶ¶éd×ÍA
C±Ì~ÂÌãÊɶ¶éd×ÍA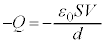 ......[]
......[]
(b) ½sÂRfT[É~¦çê½ÃdGlM[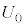 ÍA
ÍA 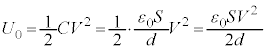 ......[]
......[]
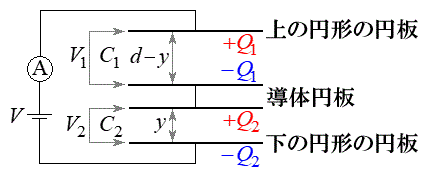 [B]@±Ì~ÂÌã¤ÉÅ«éÉÂÔu
[B]@±Ì~ÂÌã¤ÉÅ«éÉÂÔu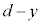 ÌRfT[ÌÃdeÊ
ÌRfT[ÌÃdeÊ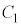 ÍA
ÍA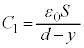 C±Ì~Â̺¤ÉÅ«éÉÂÔuyÌRfT[ÌÃdeÊ
C±Ì~Â̺¤ÉÅ«éÉÂÔuyÌRfT[ÌÃdeÊ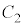 ÍA
ÍA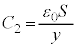 CE}Ìæ¤ÉA
CE}Ìæ¤ÉA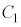 ª~¦éd×ð
ª~¦éd×ð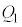 C
C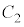 ª~¦éd×ð
ª~¦éd×ð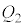 C
C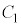 ÌÉÂÔd³ð
ÌÉÂÔd³ð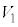 C
C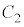 ÌÉÂÔd³ð
ÌÉÂÔd³ð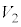 Æ·éÆA
Æ·éÆA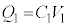 C
C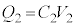 CܽA
CܽA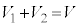 @¥¥¥@
@¥¥¥@³ÄA±Ì~ªºÌ~`~ÂÆÚGµÄ¢Ä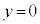 Å éÆ«©çAÍ©É
Å éÆ«©çAÍ©É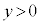 ÆÈèA±Ì~ÂƺÌ~`~ÂÆÌÚGªØêéuÔðl¦Ü·B±ÌÆ«AãÌ~`~ÂƱÌ~ÂÌÔÌRfT[ÌÃdeÊÍܾ[A]ÌCÌÜÜ(
ÆÈèA±Ì~ÂƺÌ~`~ÂÆÌÚGªØêéuÔðl¦Ü·B±ÌÆ«AãÌ~`~ÂƱÌ~ÂÌÔÌRfT[ÌÃdeÊÍܾ[A]ÌCÌÜÜ(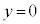 ÌÆ«Ì
ÌÆ«Ì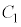 )Å·BRfT[ÉÍd×Qª~¦çêÄ¢éÌÅAãÌ~`~ÂÉÍ
)Å·BRfT[ÉÍd×Qª~¦çêÄ¢éÌÅAãÌ~`~ÂÉÍ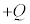 CºÌ~`~ÂÉÍ
CºÌ~`~ÂÉÍ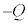 Ìdת èAÚGªØê½uÔÉà±Ì~ÂÉÍ
Ìdת èAÚGªØê½uÔÉà±Ì~ÂÉÍ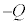 ÌdתcèÜ·B]ÁÄÚGªØê½Èã±Ì~ªãµÄ¢éÔA±Ì~ÂÉͱÌ
ÌdתcèÜ·B]ÁÄÚGªØê½Èã±Ì~ªãµÄ¢éÔA±Ì~ÂÉͱÌ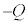 ÌdתcèÜ·(¬eÊÌö®ðQÆ)BÂÜèA
ÌdתcèÜ·(¬eÊÌö®ðQÆ)BÂÜèA 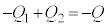 @¥¥¥A
@¥¥¥AÅ·B@ÍA
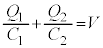 @¥¥¥B
@¥¥¥BÆÈèÜ·ªAACBðA§µAA{B~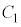 Æ·éÆA
Æ·éÆA 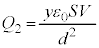 @¥¥¥C
@¥¥¥C
AæèA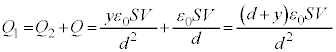 @¥¥¥D
@¥¥¥D (c) ±Ì~ÂÌãÊɶ¶éd×ÍA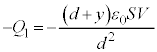 ......[]
......[] ±Ì~Â̺Êɶ¶éd×ÍA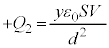 ......[]
......[]
yª0©çdÜÅÏ»·éÆA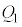 F
F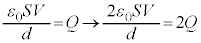 C
C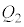 F
F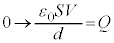 ÆÏ»µÜ·B
ÆÏ»µÜ·B
(d) ãºÌÉÂƱÌ~ÂÅ\¬³êé½sÂRfT[É~¦çê½SÃdGlM[UÍACCDæèA
(e) ±Ì~ÂÌ㸬xðvÆ·éÆA±Ì~ÂÌ^®GlM[Í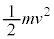 Å·BèðúµÄ©ç㸵½£ðyÆ·éÆA
Å·BèðúµÄ©ç㸵½£ðyÆ·éÆA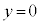 ÌÊuðîƵÄA±Ì~ÂÌÊuGlM[Í
ÌÊuðîƵÄA±Ì~ÂÌÊuGlM[Í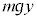 Å·B
Å·B èðúµÄ©ç£y㸷éÜÅɱÌ~ÂÌÃdGlM[Í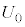 ©çUÜÅÏ»µÜ·B
©çUÜÅÏ»µÜ·B
ãÌ~`~ÂƺÌ~`~ª¼¬d¹ÉÚ±³êÄ¢éÌÅA±Ì~ÂÌÚ®ÆÆàÉdתڮµÄAãÌ~`~ÂƺÌ~`~ÂÌdתϻµA¼¬d¹ªdð·é±ÆÉӵܷBÚ®µ½d×ÍA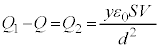 Å·B¼¬d¹ªµ½dÍA
Å·B¼¬d¹ªµ½dÍA 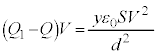 @¥¥¥E
@¥¥¥E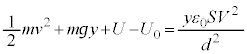 @¥¥¥F
@¥¥¥F(b)C(d)ÌÊAEðp¢ÄA
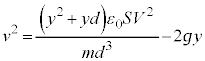 @¥¥¥G
@¥¥¥G±Ì~ÂÍã·éÌÅA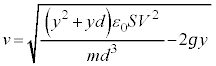 ......[]
......[]
(f) d¬vð¬êéd¬IÍAãÌ~`~ÂÌd×ÌÏ»¦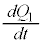 ɵ(
ɵ(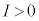 ÌÆ«d×
ÌÆ«d×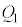 ª¦éÌÅ
ª¦éÌÅ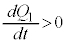 Å·)ADæèA
Å·)ADæèA 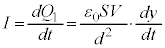 @(
@(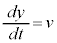 Å·)
Å·)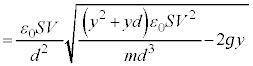 ......[]
......[]
(g) GðÏ`µÄA
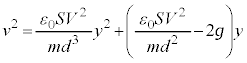 @¥¥¥H
@¥¥¥H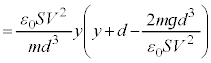 @¥¥¥I
@¥¥¥I±±ÅA¼É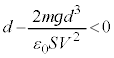 (ÂÜè
(ÂÜè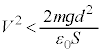 )¾Æ·éÆA
)¾Æ·éÆA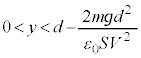 ÌÆ«É
ÌÆ«É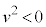 ÉÈÁĵܢܷB±Ì~ªã·é(
ÉÈÁĵܢܷB±Ì~ªã·é(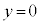 ÌÆ«
ÌÆ«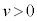 )½ßÉÍAÈÆà
)½ßÉÍAÈÆà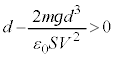 (ÂÜè
(ÂÜè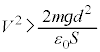 )Å éKvª èÜ·B
)Å éKvª èÜ·B
Hðt Å÷ª·éÆ(¬ÖÌ÷ª@ðQÆ)A 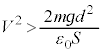 Å êÎA
Å êÎA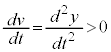 Å·B±Ì~ªã·é±Æ(
Å·B±Ì~ªã·é±Æ(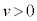 )Æí¹ÄAãµÄ¢éÔ̱Ì~ÂÌy-t OtͺÉÊ(ÖÌÊðQÆ)ÅAÁ·éÈüÉÈèÜ·B
)Æí¹ÄAãµÄ¢éÔ̱Ì~ÂÌy-t OtͺÉÊ(ÖÌÊðQÆ)ÅAÁ·éÈüÉÈèÜ·B
ã𱯽±Ì~ÂÍâªÄAãÌ~`~ÂÉÕ˵ܷBÕ˵½_ÅARfT[Í[A]Ư¶óµÆÈèÜ·B±ÌãA±Ì~Âͺ~ðnßÜ·B[B]Ì}ÅA±Ì~ÂÍãÌ~`~ÂÉÚGµÄ¢½Æ±ë©çº~·éÌÅA±Ì~ªº~µÄ¢éÔ(ºÌ~`ÉÂÌãÊ©ç±Ì~ÂÜÅÌ£ªd©çyÉÈéÜÅ)A±Ì~ÂÉcéd×Í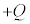 Å·BAÍA
Å·BAÍA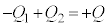 @¥¥¥J
@¥¥¥JÆÈèÜ·B@CBÍÏíç¸AJÆA§µÄðÆA±Ì~ªº~µÄ¢éÔA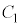 C
C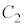 ª~¦Ä¢éd×ÍA
ª~¦Ä¢éd×ÍA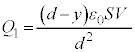 C
C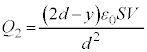 Cyªd©ç0ÜÅÏ»·éÆA
Cyªd©ç0ÜÅÏ»·éÆA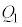 F
F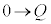 C
C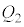 F
F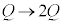 ÆÏ»µÜ·B
ÆÏ»µÜ·B
ÃdGlM[ÍA ÆÈèÜ·B
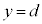 ÌÆ«©çÌdÍÌÊuGlM[ÌÏ»Í
ÌÆ«©çÌdÍÌÊuGlM[ÌÏ»Í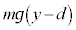 C
C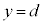 ÌÆ«ÌÃdGlM[Í(b)Ì
ÌÆ«ÌÃdGlM[Í(b)Ì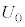 ÅAÃdGlM[ÌÏ»ÍFƯlÉ
ÅAÃdGlM[ÌÏ»ÍFƯlÉ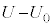 Å·B±ÌÔÉã¤~`É©缬d¹©çã¤~`ÉÂÉÚ®µ½d×Í
Å·B±ÌÔÉã¤~`É©缬d¹©çã¤~`ÉÂÉÚ®µ½d×Í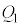 Å·(
Å·(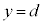 űÌ~ª£ê½uÔÉã¤~`~ÂÌd×
űÌ~ª£ê½uÔÉã¤~`~ÂÌd×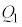 Í0ÉÈé)B
Í0ÉÈé)B
¼¬d¹ªµ½dÍA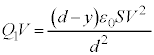
±Ì~º~ÉAGlM[Ì´Ì®FÍA ÆÈèAGÍA
ÆÈèÜ·BKðt Å÷ª·éÆA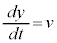 æèA
æèA yªd©ç0ÜÅÏ»·éÔÍ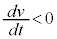 ÅA±Ì~ªº~µÄ¢éÔ(
ÅA±Ì~ªº~µÄ¢éÔ(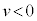 )̱Ì~ÂÌy-t OtÍãÉÊŸ·éÈüÉÈèÜ·B
)̱Ì~ÂÌy-t OtÍãÉÊŸ·éÈüÉÈèÜ·B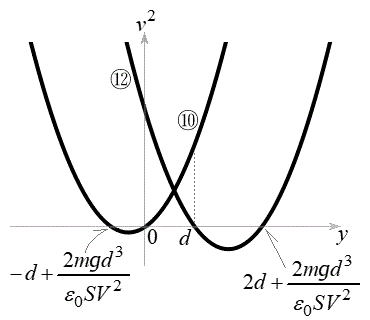
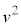 -yÌOtðã¸ÌIƺ~ÌKÆÅär·éÆAIÅÍy²Æ
-yÌOtðã¸ÌIƺ~ÌKÆÅär·éÆAIÅÍy²Æ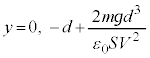 (
(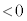 C
C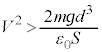 Ƶܷ)ÆÅðíèÜ·ªAKÅÍA
Ƶܷ)ÆÅðíèÜ·ªAKÅÍA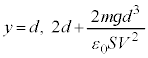 ÆÅðíèÜ·By²ÆÌ2ð_Ì£ðä×éÆAIÅÍ
ÆÅðíèÜ·By²ÆÌ2ð_Ì£ðä×éÆAIÅÍ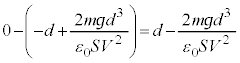 CKÅÍ
CKÅÍ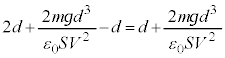 ÆÈèAKÌûªå«ÈèÜ·B
ÆÈèAKÌûªå«ÈèÜ·B
]ÁÄAã¸ÅyF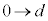 ÆÈéÆ«Ì
ÆÈéÆ«Ì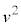 ƺ~ÅyF
ƺ~ÅyF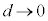 ÆÈéÆ«Ì
ÆÈéÆ«Ì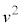 Ìlðär·éÆAº~Ìûªå«ÈèÜ·BÆ¢¤±ÆÍA±Ì~ªA㸵ÄãÌ~`ÉÂÉÕË·éÜÅÌÔ
Ìlðär·éÆAº~Ìûªå«ÈèÜ·BÆ¢¤±ÆÍA±Ì~ªA㸵ÄãÌ~`ÉÂÉÕË·éÜÅÌÔ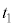 ƺ~µÄºÌ~`ÉÂÉÕË·éÜÅÌÔ
ƺ~µÄºÌ~`ÉÂÉÕË·éÜÅÌÔ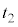 ðä×éÆAº~·éûª¬¢ÌÅA
ðä×éÆAº~·éûª¬¢ÌÅA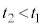 ÆÈèÜ·B
ÆÈèÜ·B
ÈãæèAtÆ£yÌÖWðƵÄÅàÓ³íµ¢OtÍ@ ......[]
yLz±±©çLÅ·B²ÌF³Ü̲x²ððè½Aæ뵨袢½µÜ·B
yLzLͱ±ÜÅÅ·B
@@Èwå¨TOP@@¨TOP@@TOPy[WÉßé
yLz±±©çLÅ·B²ÌF³Ü̲x²ððè½Aæ뵨袢½µÜ·B
yLzLͱ±ÜÅÅ·B
eâèÌì Í
oèåwÉ®µÜ·BȨAðÍA
êwywm§ìÅ·B©2005-2025(L)èéçé êwywm üïótInåwó±lbgmêwywm(²Äàͱ¿ç)²üïÍA
ܸA±¿çÜÅ[ð
¨è¾³¢B 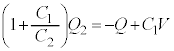
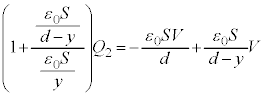
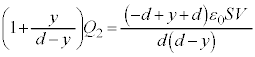
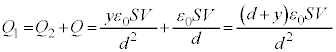 @¥¥¥D
@¥¥¥D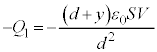 ......[]
......[]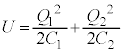
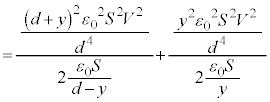
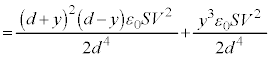
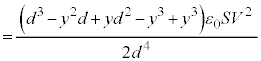
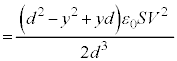 ......[]
......[]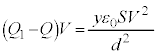 @¥¥¥E
@¥¥¥E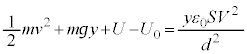 @¥¥¥F
@¥¥¥F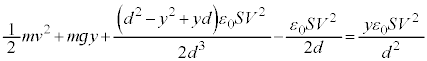
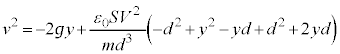
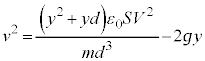 @¥¥¥G
@¥¥¥G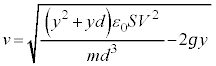 ......[]
......[]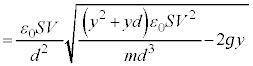 ......[]
......[]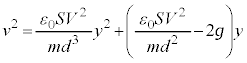 @¥¥¥H
@¥¥¥H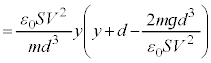 @¥¥¥I
@¥¥¥I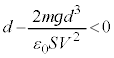 (ÂÜè
(ÂÜè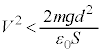 )¾Æ·éÆA
)¾Æ·éÆA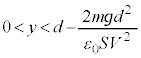 ÌÆ«É
ÌÆ«É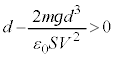 (ÂÜè
(ÂÜè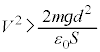 )Å éKvª èÜ·B
)Å éKvª èÜ·B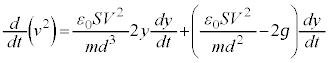
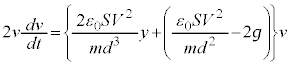
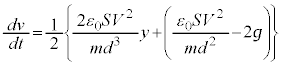
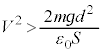 Å êÎA
Å êÎA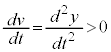 Å·B±Ì~ªã·é±Æ(
Å·B±Ì~ªã·é±Æ(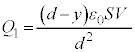 C
C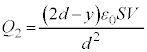 C
C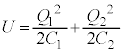
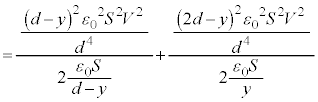
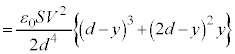
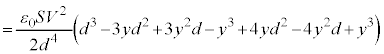
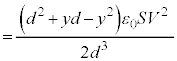
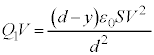
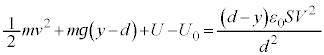
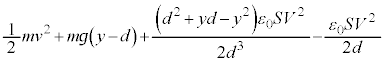
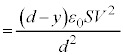
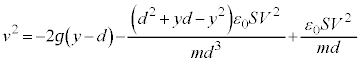
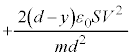
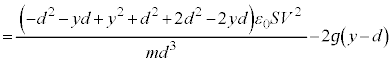
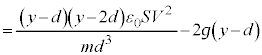
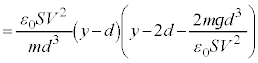 @¥¥¥K
@¥¥¥K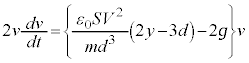
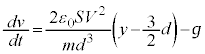
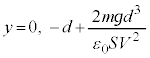 (
(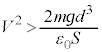 Ƶܷ)ÆÅðíèÜ·ªAKÅÍA
Ƶܷ)ÆÅðíèÜ·ªAKÅÍA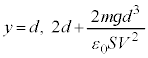 ÆÅðíèÜ·By²ÆÌ2ð_Ì£ðä×éÆAIÅÍ
ÆÅðíèÜ·By²ÆÌ2ð_Ì£ðä×éÆAIÅÍ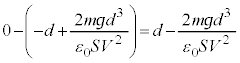 CKÅÍ
CKÅÍ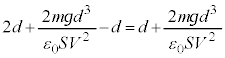 ÆÈèAKÌûªå«ÈèÜ·B
ÆÈèAKÌûªå«ÈèÜ·B