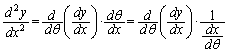�d�ʑ吔�w'08�N���[2]
��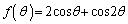 �C
�C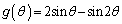 ��p����
��p����
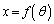 �C�@
�C�@
(1)  �ɑΉ�����C��̓_�̍��W�����߂�B
�ɑΉ�����C��̓_�̍��W�����߂�B (2) 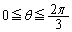 �͈̔͂�
�͈̔͂�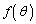 ��
�� �̑����ׁA�Ȑ�C��
�̑����ׁA�Ȑ�C�� �ɑΉ����镔���̊T�`��`���B
�ɑΉ����镔���̊T�`��`���B (3) C��̓_��x���Ɋւ��đΏ̈ړ������C��̓_�Ɉڂ邱�Ƃ������B
(4) C��̓_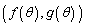 �����_�𒆐S�Ƃ���
�����_�𒆐S�Ƃ���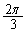 ������]����ƁAC��̓_
������]����ƁAC��̓_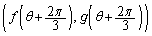 �Ɉڂ邱�Ƃ������B
�Ɉڂ邱�Ƃ������B (5) �Ȑ�C�̊T�`��`���AC�ň͂܂�镔���̖ʐ�S�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
 ���@�Ȑ�C��̓_P
���@�Ȑ�C��̓_P �̍��W�́A
�̍��W�́A
�Ə�����̂ŁA���a2�̉~����̓_Q �C
�C �Ƃ��āA
�Ƃ��āA
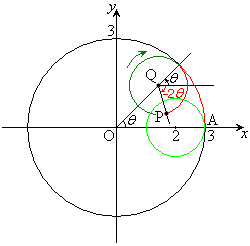
�ł��B�Ȑ�C�́A�E�}�̂悤�ɁA���a3�̉~�� �̓��������邱�ƂȂ��ڐG��ۂ��Ȃ���]���锼�a1�̉~
�̓��������邱�ƂȂ��ڐG��ۂ��Ȃ���]���锼�a1�̉~ (�͂��߉E�}A��
(�͂��߉E�}A��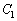 �Ɛڂ��Ă���)��̓_P(�͂���A�ɂ���)���`���Ȑ��ł��B�n�C�|�T�C�N���C�h�ƌĂ�Ă��܂��B
�Ɛڂ��Ă���)��̓_P(�͂���A�ɂ���)���`���Ȑ��ł��B�n�C�|�T�C�N���C�h�ƌĂ�Ă��܂��B
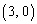 ......[��]
......[��]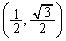 ......[��]
......[��] ......[��]
......[��]
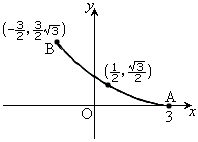 �@θ ��
�@θ ��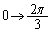 �̂Ƃ��Ax���W�͌�����y���W�͑�������(���̑������Q��)�̂ŁA�_P��
�̂Ƃ��Ax���W�͌�����y���W�͑�������(���̑������Q��)�̂ŁA�_P��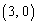 ����
���� �܂ŁA����Ɍ������Đi��ł����܂��B
�܂ŁA����Ɍ������Đi��ł����܂��B
�Ȑ�C�� �ɑΉ����镔���̊T�`�͉E�}�����B
�ɑΉ����镔���̊T�`�͉E�}�����B
(3) C��̓_��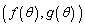 �ƕ\����̂ŁAC��̓_
�ƕ\����̂ŁAC��̓_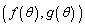 ��C��Ɉڂ�Ƃ������Ƃ́A�ڂ�����̓_��
��C��Ɉڂ�Ƃ������Ƃ́A�ڂ�����̓_��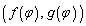 �Ƃ����`�ɏ�����A�Ƃ������Ƃł��B
�Ƃ����`�ɏ�����A�Ƃ������Ƃł��B C��̓_ ��x���Ɋւ��đΏ̈ړ������
��x���Ɋւ��đΏ̈ړ������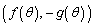 �Ɉڂ�܂��B
�Ɉڂ�܂��B �ƂȂ�̂ŁA�ڂ������C��̓_�ł��B�܂�AC��̓_��x���Ɋւ��đΏ̈ړ������C��̓_�Ɉڂ�܂��B
(4) ���_�𒆐S�Ƃ���p �̉�]��\���s��́A
�̉�]��\���s��́A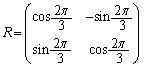 �ł�(1���ϊ����Q��)�B
�ł�(1���ϊ����Q��)�B ���̉�]�ړ��ɂ���āAC��̓_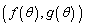 �́A
�́A �����ŁA2���ڂ̕����A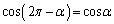 �C
�C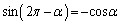 ���g���A
���g���A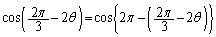
�ƕό`����ƁA
�ƂȂ�̂ŁAC��̓_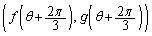 �Ɉڂ�܂��B
�Ɉڂ�܂��B 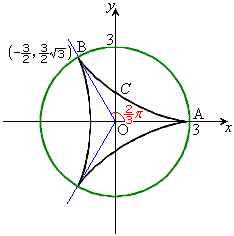
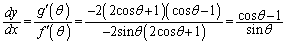 �@����@
�@����@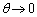 �̂Ƃ��A�Ȑ�C�̐ڐ��̌X���́A
�̂Ƃ��A�Ȑ�C�̐ڐ��̌X���́A���A0�ɋ߂Â��܂��B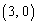 ��ʂ�X��0�̒����́A
��ʂ�X��0�̒����́A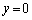 �C�܂�Ax���ł��B
�C�܂�Ax���ł��B
 �̂Ƃ��A�Ȑ�C�̐ڐ��̌X���́A
�̂Ƃ��A�Ȑ�C�̐ڐ��̌X���́A ���A �ɋ߂Â��܂��B
�ɋ߂Â��܂��B ��ʂ�X��
��ʂ�X��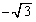 �̒����F
�̒����F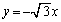 �͌��_��ʂ�܂��B(4)����l����ƁA���̓_�ŋȐ�C�͐���Ă���(��_�ƌ����܂�)���Ƃ��킩��܂��B�܂��A�_
�͌��_��ʂ�܂��B(4)����l����ƁA���̓_�ŋȐ�C�͐���Ă���(��_�ƌ����܂�)���Ƃ��킩��܂��B�܂��A�_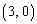 �C�_
�C�_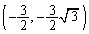 ����_�ł��B�Ȑ�C�̊T�`�͉E�}�����B
����_�ł��B�Ȑ�C�̊T�`�͉E�}�����B
���D��L�Łu �C
�C �̂Ƃ��̐ڐ��̌X���v�Ƃ��Ȃ��̂́A
�̂Ƃ��̐ڐ��̌X���v�Ƃ��Ȃ��̂́A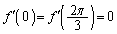 �ŁA
�ŁA �C
�C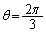 �ɂ����āA�}��ϐ��\�����ꂽ���F
�ɂ����āA�}��ϐ��\�����ꂽ���F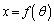 �C
�C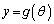 �@(x�̊�y)�́A�����\�ł͂Ȃ�����ł��B�܂��A���ʂ����ׂ邽�߂ɁA
�@(x�̊�y)�́A�����\�ł͂Ȃ�����ł��B�܂��A���ʂ����ׂ邽�߂ɁA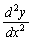 ���v�Z���Ă݂܂��B�}��ϐ��\�����ꂽ���ł́A�H�v���K�v�ł��B
���v�Z���Ă݂܂��B�}��ϐ��\�����ꂽ���ł́A�H�v���K�v�ł��B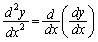 �ł����A�@������ƁA
�ł����A�@������ƁA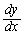 ��θ �̊��̌`�ŕ\����Ă���̂ŁA�������̔����@���g���āAθ �Ŕ������A
��θ �̊��̌`�ŕ\����Ă���̂ŁA�������̔����@���g���āAθ �Ŕ������A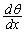 ����ł����邱�ƂɂȂ�܂��B
����ł����邱�ƂɂȂ�܂��B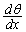 �́A�t���̔����@�̌������A
�́A�t���̔����@�̌������A �ł��B
�ł��B 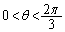 �ɂ����ẮA(2)��
�ɂ����ẮA(2)��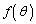 �̑����\���
�̑����\��� �Ȃ̂ŁA
�Ȃ̂ŁA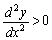 ���A�Ȑ�C�͉��ɓʂł��B�������ł́A�����܂Œ��ׂȂ��Ă��A
���A�Ȑ�C�͉��ɓʂł��B�������ł́A�����܂Œ��ׂȂ��Ă��A �ɑΉ�����C��̓_����T�`��`�����Ƃ��ł���ł��傤�B
�ɑΉ�����C��̓_����T�`��`�����Ƃ��ł���ł��傤�B
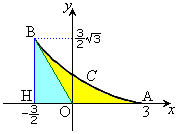
�ʐς́A�Ȑ�C�̑Ώ̐��𗘗p���āA�E�}�ŁA�Ȑ�C�Ɛ���OA�C����OB�ň͂܂�镔��(���F���F����)�̖ʐ� ��3�{���邱�Ƃɂ��܂��B
��3�{���邱�Ƃɂ��܂��B �͋Ȑ�C��
�͋Ȑ�C��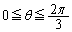 �̕�����x���A����
�̕�����x���A����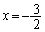 �ň͂܂�镔���̖ʐ�
�ň͂܂�镔���̖ʐ�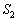 ����E�}�̎O�p�`OBH(���F���F����)�̖ʐ�
����E�}�̎O�p�`OBH(���F���F����)�̖ʐ�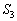 ���������Ƃɂ�苁�߂܂��B
���������Ƃɂ�苁�߂܂��Bx�Cy�Ƃ��}��ϐ�θ �ŕ\����Ă���̂ŁAθ �̐ϕ��ɕς��邽�߂��u���ϕ����܂��B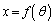 �Ƃ����ƁA
�Ƃ����ƁA �C
�C �Cx�F
�Cx�F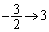 �̂Ƃ��Aθ�F
�̂Ƃ��Aθ�F
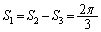
 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B