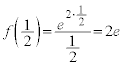�c�嗝�H���w'10�N[B1]
a�𐳂̒萔�Ƃ��A���W���ʏ�̋Ȑ�C�F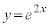 �ƒ���l�F
�ƒ���l�F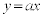 ���l����B
���l����B
(1) �Ȑ�C�ƒ���l�������P�̋��L�_A�����Ƃ��A�萔a�̒l�Ɠ_A�̍��W�����߂Ȃ����B���߂�ߒ��������Ȃ����B
(2) (1)�̂Ƃ��A�Ȑ�C�C����l�C�����y���ň͂܂��}�`��y���̂܂���1��]���Ăł����]�̂̑̐�V�����߂Ȃ����B���߂�ߒ��������Ȃ����B
(3) a��(1)�ŋ��߂��l��菬�������̒萔�Ƃ���B���̂Ƃ��A����l�F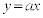 �͋Ȑ�C�Ƌ��L�_�������Ȃ��B�_P���Ȑ�C����A�_Q������l����Ƃ��A����PQ�̒������ŏ��ƂȂ�̂́A�_P�̍��W��
�͋Ȑ�C�Ƌ��L�_�������Ȃ��B�_P���Ȑ�C����A�_Q������l����Ƃ��A����PQ�̒������ŏ��ƂȂ�̂́A�_P�̍��W�� �̂Ƃ��ł���B���̓_P
�̂Ƃ��ł���B���̓_P ��y����ɂ���̂�
��y����ɂ���̂� �̂Ƃ��ł���A���̂Ƃ��ŏ��̐����̒��������߂��
�̂Ƃ��ł���A���̂Ƃ��ŏ��̐����̒��������߂��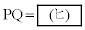 �ƂȂ�B
�ƂȂ�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���̖������ȏ��̗�背�x���̖��ł��B(3)��[A3]�Ɠ����|�̖��ł��B
(1) �Ȑ�C�͉��ɓʂȋȐ��Ȃ̂ŁA�Ȑ�C�ƒ���l������1�̋��L�_�����Ƃ��A����l�͋Ȑ�C���ڐ��ɂȂ��Ă��܂��B C�F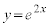
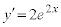
����l��C�̐ڐ��ɂȂ�Ƃ��A�ڐ��̌X����a�Ȃ̂ŁA
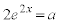 �@����@
�@����@�� 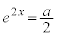 �ړ_��C��̓_�ł����Ă���l��̓_�Ȃ̂ŁA����y���W�ɂ��āA
�ړ_��C��̓_�ł����Ă���l��̓_�Ȃ̂ŁA����y���W�ɂ��āA 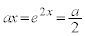 �@����A
�@����A����āA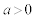 ���A�ړ_��x���W�́A
���A�ړ_��x���W�́A �ڐ��̌X��a�́A�@���A
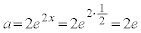 ......[��]
......[��]�ړ_��y���W�́A�A���A
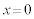 �͂�������Ȃ��̂ŁAx�Ŋ����āA
�͂�������Ȃ��̂ŁAx�Ŋ����āA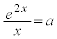 �@����B
�@����BC��l������1�̋��L�_�����Ƃ��A�������B������1�̎������������A���̎����������L�_��x���W�ɂȂ�܂��B
�Ƃ����āA
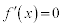 �Ƃ���ƁA
�Ƃ���ƁA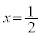
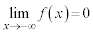 �C
�C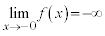 �C
�C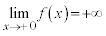 �C
�C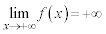 ���(���̑������Q��)�A
���(���̑������Q��)�A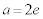 �̂Ƃ��������B�͂���1�̎�����
�̂Ƃ��������B�͂���1�̎�����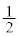 �������A�ړ_��x���W��
�������A�ړ_��x���W��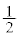 �ɂȂ�܂��B
�ɂȂ�܂��B
(2) (1)�̂Ƃ��A����l�́A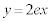 �ƂȂ�܂��B���߂�̐�V�́A��ʂ����a
�ƂȂ�܂��B���߂�̐�V�́A��ʂ����a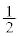 �̉~�ō���e�̉~���̑̐ς���A�Ȑ�C��y���ƒ���
�̉~�ō���e�̉~���̑̐ς���A�Ȑ�C��y���ƒ���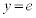 �ň͂܂�镔����y���̂܂��ɉ�]��������]�̂̑̐ς����������̂ɂȂ�܂�(y���̂܂��̉�]�����Q��)�B
�ň͂܂�镔����y���̂܂��ɉ�]��������]�̂̑̐ς����������̂ɂȂ�܂�(y���̂܂��̉�]�����Q��)�B �� 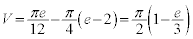 ......[��]
......[��]
(3) ����PQ�̒������ŏ��ɂȂ�̂́AP�ɂ����ċȐ�C�ɌX��a�̐ڐ���������Ƃ��ŁA(1)�̇@�C�A�Ɠ��l�ɂ��āA�ړ_��y���W�́A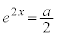
���̗��ӂ̑ΐ����l����ƁA
�ړ_��x���W�́A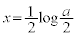
����PQ�̒������ŏ��ƂȂ�Ƃ���P�̍��W�́A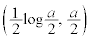 ......[��]�_P��y����ɂ����x���W��0�ŁA
......[��]�_P��y����ɂ����x���W��0�ŁA �� 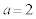 ......[��]���̂Ƃ��AP�̍��W��
......[��]���̂Ƃ��AP�̍��W��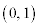 �C�ŏ��̐����̒����́AP
�C�ŏ��̐����̒����́AP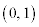 �ƒ���l�F
�ƒ���l�F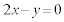 �Ƃ̋����Ƃ��āA
�Ƃ̋����Ƃ��āA
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B