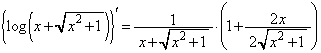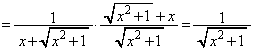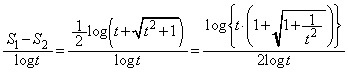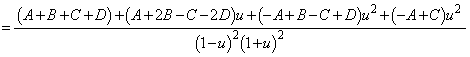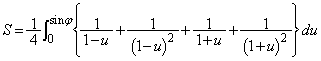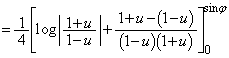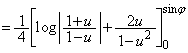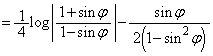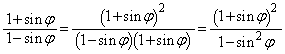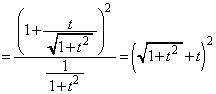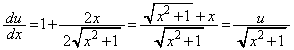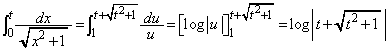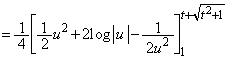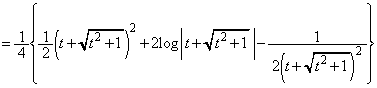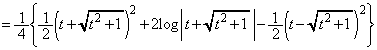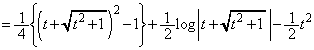���H�吔�w'11�N���[2]
���̎�
�ŕ\�����xy���ʏ�̋Ȑ�C���l����B�萔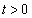 �ɑ��A�_P
�ɑ��A�_P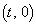 ��ʂ�Ax���ɐ����Ȓ���
��ʂ�Ax���ɐ����Ȓ���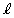 �ƋȐ�C�̌�_��Q�Ƃ���B�Ȑ�C�Cx���Cy������ђ���
�ƋȐ�C�̌�_��Q�Ƃ���B�Ȑ�C�Cx���Cy������ђ���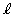 �ň͂܂ꂽ�}�`�̖ʐς�
�ň͂܂ꂽ�}�`�̖ʐς�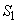 �Ƃ��A��OPQ�̖ʐς�
�Ƃ��A��OPQ�̖ʐς�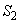 �Ƃ���B
�Ƃ���B
(1) 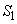 �C
�C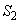 ��t��p���ĕ\���B
��t��p���ĕ\���B (2) �Ɍ�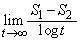 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�p�o�̒�ϕ�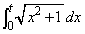 �Ɋւ�����ł��B���낢��Ȍv�Z�@������܂����A�NjL�ŏڂ����������Ă݂܂��B
�Ɋւ�����ł��B���낢��Ȍv�Z�@������܂����A�NjL�ŏڂ����������Ă݂܂��B
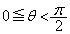 ���
���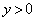 �Ȃ̂ŁA
�Ȃ̂ŁA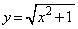 �@����@
�@����@
����āAQ�̍��W��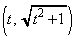
�O�p�`OPQ�́A���t�C����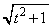 ���A�ʐ�
���A�ʐ�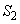 �́A
�́A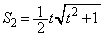 ......[��]
......[��]�@��p���āA
�� 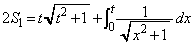
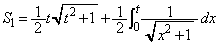 �@����B
�@����B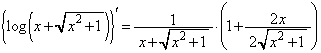
����āA�B���A
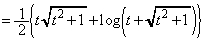 ......[��]
......[��]
(2) 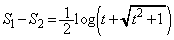
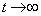 �̂Ƃ��A
�̂Ƃ��A�� 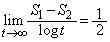 ......[��]
......[��]
�NjL�D(1)��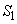 �̇A�̒�ϕ��́A�ȉ��̂悤�Ɍv�Z���邱�Ƃ��ł��܂��B
�̇A�̒�ϕ��́A�ȉ��̂悤�Ɍv�Z���邱�Ƃ��ł��܂��B 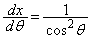 �C
�C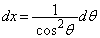 �Cx�F
�Cx�F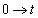 �̂Ƃ��Aθ�F
�̂Ƃ��Aθ�F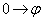 (�������A
(�������A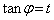 �C
�C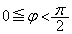 )�@(�u���ϕ����Q��)
)�@(�u���ϕ����Q��)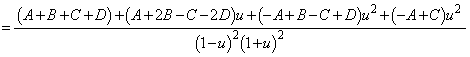
�Ƃ����ƁA
�� 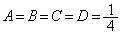
�C�ɑ�����āA
(1)�̒�ϕ�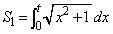 �ɂ��ẮA[��]�̂悤�ɕ����ϕ��@�Ƒg�ݍ��킹�Čv�Z����̂��悢�Ǝv���܂����A
�ɂ��ẮA[��]�̂悤�ɕ����ϕ��@�Ƒg�ݍ��킹�Čv�Z����̂��悢�Ǝv���܂����A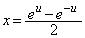 �Ƃ����Ēu���ϕ����邱�Ƃ��ł��܂�(���嗝�H'10�N[4]���Q��)�B
�Ƃ����Ēu���ϕ����邱�Ƃ��ł��܂�(���嗝�H'10�N[4]���Q��)�B
�ł����A������ɂ���A���Ȃ�v�Z���ʓ|�ł��B
�����ł́A���Ȃ�Z�I�I�ɉ߂��܂����A���N�Ɍv�Z�ł���Z�I���Љ�Ă����܂��傤�B���嗝�n'10�N[4]�̖��ɐ��荞�܂�Ă���l�����ł�(���嗝�n10�N�O�������[4]�̌������Q�Ƃ��Ă�������)�B 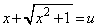 �@����D
�@����D�Ƃ����܂��B
x�F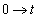 �̂Ƃ��Au�F
�̂Ƃ��Au�F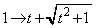
���̒u���ɂ��A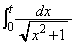 �ł���A
�ł���A �Ƃ����Ɍv�Z�ł��܂��B
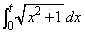 �̏ꍇ�́A���X�H�v���܂��B
�̏ꍇ�́A���X�H�v���܂��B ���A
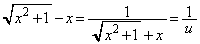 �@����E
�@����E�D�{�E���A
������A
�Ƃ��邱�Ƃ��ł��܂����A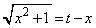 �Ƃ��āA�ȉ��̂悤�ɂ���Ƃ����ƃ��N�ɍs���܂��B
�Ƃ��āA�ȉ��̂悤�ɂ���Ƃ����ƃ��N�ɍs���܂��B 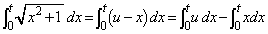 �@(�������|�C���g)
�@(�������|�C���g)��1�������u���ϕ����āA
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B