���H�吔�w'22�N�O��[3]
α��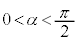 ���������Ƃ���B
���������Ƃ���B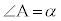 �����
�����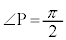 �������p�O�p�`APB���A����2�̏���(a)�C(b)�����Ȃ���A����
�������p�O�p�`APB���A����2�̏���(a)�C(b)�����Ȃ���A����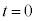 ���玞��
���玞��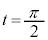 �܂�xy���ʏ���Ƃ���B
�܂�xy���ʏ���Ƃ���B
(a) ����t �ł̓_A�CB�̍��W�́A���ꂼ��A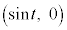 �CB
�CB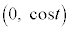 �ł���B
�ł���B (b) �_P�͑��ی����ɂ���B
���̂Ƃ��A���̖₢�ɓ�����B
(1) �_P�͂��钼��������Ƃ������A���̒����̕�������α��p���ĕ\���B
(2) ����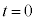 ���玞��
���玞��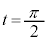 �܂ł̊Ԃɓ_P���������̂��α��p���ĕ\���B
�܂ł̊Ԃɓ_P���������̂��α��p���ĕ\���B
(3) xy���ʓ��ɂ����āA�A���s����
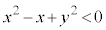 �C
�C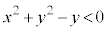
�ɂ���܂�̈��D�Ƃ���B���̂Ƃ��A�_P�͗̈�D�ɂ͓���Ȃ����Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�_A��ʂ钼���Ɠ_B��ʂ钼�������������̌�_��P�C�Ƃ��đ����邱�Ƃ��ł��܂����A����AP��x���ɒ�������ꍇ�����蓾��̂ŁA�����ł́A"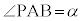 "���A���f��������ł���]�ōl���A�@�B�I�Ȍv�Z�ł��܂���A�v���[�`�ł���Ă݂܂��B
"���A���f��������ł���]�ōl���A�@�B�I�Ȍv�Z�ł��܂���A�v���[�`�ł���Ă݂܂��B
 �C
�C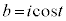 �C
�C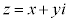 (i�͋����P�ʁAx�Cy�͎���)
(i�͋����P�ʁAx�Cy�͎���)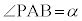 �Ə���(b)���A�_B
�Ə���(b)���A�_B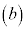 ��_A
��_A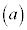 �̉��Ɋp
�̉��Ɋp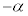 ��]��
��]��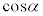 �{����ƁA�_P
�{����ƁA�_P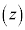 �ɗ��܂��B����āA
�ɗ��܂��B����āA����āA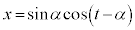 �C
�C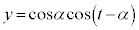 �@����@
�@����@
������A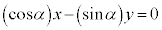 �@����A
�@����A
����āA�_P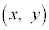 �͒�����̓_�ŁA�����̕������́A
�͒�����̓_�ŁA�����̕������́A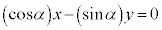 ......[��]
......[��] ���D�������ē����o�Ă��܂��ƁA�����ƊȒP�ȉ�@�����邱�ƂɋC�t���܂��B�����̕��������A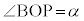 �ƌ����Ă���킯�ŁA
�ƌ����Ă���킯�ŁA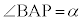 �Ȃ̂ŁA�~���p�ōs�����Ƃ������Ƃł��B�������ōŏ����炱�̂��ƂɋC�t����A
�Ȃ̂ŁA�~���p�ōs�����Ƃ������Ƃł��B�������ōŏ����炱�̂��ƂɋC�t����A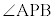 ��
��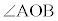 ���Ƃ��ɒ��p�ł��邱�Ƃ���A4�_O�CA�CP�CB�͓���~����ŁA�~���p�̒藝���
���Ƃ��ɒ��p�ł��邱�Ƃ���A4�_O�CA�CP�CB�͓���~����ŁA�~���p�̒藝���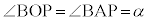 �ň��Ȃ̂ŁA�_P�́A����OB�Ɗpα���Ȃ���1�ی����ʂ钼����ɂ���A�����̌X����
�ň��Ȃ̂ŁA�_P�́A����OB�Ɗpα���Ȃ���1�ی����ʂ钼����ɂ���A�����̌X����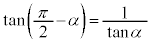 �Œ����̕�������
�Œ����̕������� �ƊȒP�ɉł��܂��B
�ƊȒP�ɉł��܂��B
(2) �@��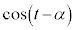 ��
��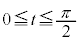 �ɂ����Ăǂ̂悤�ȕω�������̂�(�O�p���̃O���t���Q��)�ׂ�悢�̂ł����A
�ɂ����Ăǂ̂悤�ȕω�������̂�(�O�p���̃O���t���Q��)�ׂ�悢�̂ł����A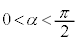 ���A�͈́F
���A�͈́F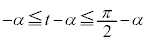 �́A
�́A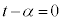 ���܂݁A���̂Ƃ�
���܂݁A���̂Ƃ� �ł��B�]���āA
�ł��B�]���āA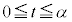 �ɂ����Ă�
�ɂ����Ă�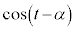 ��
��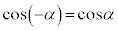 ����1�܂��P���ɑ������A
����1�܂��P���ɑ������A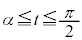 �ɂ����Ă�
�ɂ����Ă�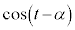 ��1����
��1����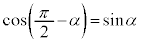 �܂��P���Ɍ������܂��B�@���(��)
�܂��P���Ɍ������܂��B�@���(��) �܂�A�����A�ɉ����ē_P�́A����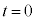 ���玞��
���玞��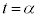 �܂ŁA�_
�܂ŁA�_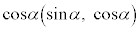 ����_
����_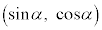 �܂œ����A���̓��̂��
�܂œ����A���̓��̂�� �ł��B����
�ł��B����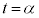 ���玞��
���玞��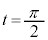 �܂ŁA�_
�܂ŁA�_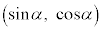 ����_
����_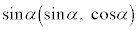 �܂ň����Ԃ��A���̓��̂��
�܂ň����Ԃ��A���̓��̂��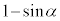 �ł��B
�ł��B
�ȏ���A�_P���������̂�́A 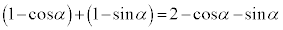 ......[��]
......[��]
(3) �@�̕s������^�s�����ɑ�����Ă݂�ƁA
(2)�Ō��������悤�ɁA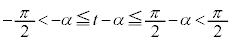 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA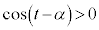 �ł��B(2)��(��)���A
�ł��B(2)��(��)���A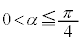 �ɂ����Ă�
�ɂ����Ă�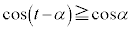 ���
���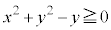 �C
�C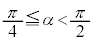 �ɂ����Ă�
�ɂ����Ă�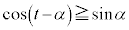 ���
���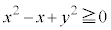
����āA�_P�͗̈�D�ɓ��邱�Ƃ͂���܂���(�s�����̕\���̈����Q��)�B ���D�A���s�����F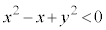 �C
�C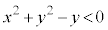 �ɂ���܂��̈�D�Ƃ����̂́A
�ɂ���܂��̈�D�Ƃ����̂́A ���A�B���C�C�܂�A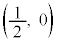 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a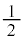 �̉~���������ł����Ă���
�̉~���������ł����Ă���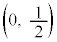 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a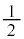 �̉~���������A�ł��B
�̉~���������A�ł��B
��L�̉ł́A�_P�̍��W���A�B�܂��͇C�̂����ꂩ�����Ȃ��A�Ƃ������Ƃ������܂����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B