���H�吔�w'23�N�O��[4]
xyz��Ԃɂ����āAx�������Ƃ��锼�a2�̉~������A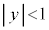 ����
����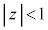 �ŕ\�����p���̓�������菜�������̂�A�Ƃ���B�܂��AA��x���̂܂���
�ŕ\�����p���̓�������菜�������̂�A�Ƃ���B�܂��AA��x���̂܂���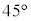 ��]���Ă���z���̂܂���
��]���Ă���z���̂܂���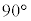 ��]�������̂�B�Ƃ���BA��B�̋��ʕ����̑̐ς����߂�B
��]�������̂�B�Ƃ���BA��B�̋��ʕ����̑̐ς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�����������̂̑̐ς����߂���ł́A�ǂ����Ă��A�ǂ�ȗ��̂ɂȂ�̂��낤�A�ƁA���̂̊T�`���l�������Ȃ���̂ł��B�ł����A���̂̊T�`�����ނ��ƂɎ��Ԃ������Ă��A�Ȃ��Ȃ��v���悤�ɂ��߂܂���B
�{��̊�{���Ƃ��āA�~���̓�������菜�����ƂȂ��Ax�������Ƃ��锼�a2�̉~���ƁAy�������Ƃ��锼�a2�̉~���̋��ʕ��������߂�A�Ƃ�����肪����܂��B���̂̊T�`��c�����邱�Ƃ͍���ł����Az���ɐ����ȕ���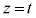 (
(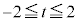 )�Ő����f�ʂ��l���邱�Ƃ͂ł��܂��B�~����
)�Ő����f�ʂ��l���邱�Ƃ͂ł��܂��B�~����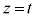 �Ő�ƁA�f�ʂ͒����`�ł��B2�̉~���̋��ʕ�����
�Ő�ƁA�f�ʂ͒����`�ł��B2�̉~���̋��ʕ�����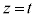 �Ő�ƁA���ʕ����̒f�ʂ�2�̓������̒����`�̋��ʕ����ƂȂ�A�f�ʂ͐����`�ɂȂ�܂��B���Ƃ͐����`�̖ʐς�ϕ�����A���̂̑̐ς��v�Z���邱�Ƃ��ł��܂��B
�Ő�ƁA���ʕ����̒f�ʂ�2�̓������̒����`�̋��ʕ����ƂȂ�A�f�ʂ͐����`�ɂȂ�܂��B���Ƃ͐����`�̖ʐς�ϕ�����A���̂̑̐ς��v�Z���邱�Ƃ��ł��܂��B
���嗝�n���w05�N[6]�ł́Ax�������Ƃ��锼�ar�̉~���ƁAz�������Ƃ��锼�ar�̉~���̋��ʕ����ɂ����y�������Ƃ��锼�ar�̉~��������ށA�Ƃ����ݒ�ɂȂ��Ă��܂��B�ƂĂ����̂̊T�`��z�����ł��܂��A��͂�f�ʂ��l�@���邱�Ƃɂ��A�ł��܂��B
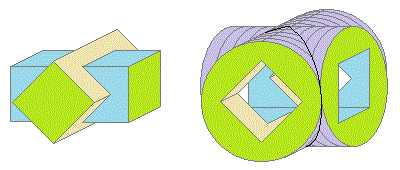 �{������̂̊T�`�́A2�̊p����������Ă��闧�̂̊T�`�A�����āA���̎�菜����镔�����l������A��B��������Ă�����l����ƁA�E�}�̂悤�ɂȂ�܂�(A��B�̋��ʕ����̐}�ł͂Ȃ��̂Œ���)�B�ł����A���̐}�����Ă��A�ǂ̂悤�ɂȂ��Ă���̂��悭�킩��܂���B�܂��A�ǂ������v�Z������Α̐ς����߂���̂��A�Ƃ������Ƃɂ��Ȃ���܂���B���̂̊T�`���l���邱�ƂɈӖ��͂Ȃ��̂ł��B
�{������̂̊T�`�́A2�̊p����������Ă��闧�̂̊T�`�A�����āA���̎�菜����镔�����l������A��B��������Ă�����l����ƁA�E�}�̂悤�ɂȂ�܂�(A��B�̋��ʕ����̐}�ł͂Ȃ��̂Œ���)�B�ł����A���̐}�����Ă��A�ǂ̂悤�ɂȂ��Ă���̂��悭�킩��܂���B�܂��A�ǂ������v�Z������Α̐ς����߂���̂��A�Ƃ������Ƃɂ��Ȃ���܂���B���̂̊T�`���l���邱�ƂɈӖ��͂Ȃ��̂ł��B
�Ƃ����킯�ŁA�{��ł��f�ʂ��l�@���邱�ƂɂȂ�܂��B2�~���̋��ʕ����̑̐ς����߂���Ɠ��l�ɁAz���ɐ����ȕ���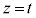 �Ő����f�ʂ��l���邱�Ƃɂ��܂��B���̂����݂��镔���ɑ�����_
�Ő����f�ʂ��l���邱�Ƃɂ��܂��B���̂����݂��镔���ɑ�����_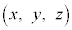 ���ǂ̂悤�ȕs���������̂����l���A�s������
���ǂ̂悤�ȕs���������̂����l���A�s������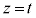 �Ƃ��āA
�Ƃ��āA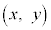 ���������s�����ׂ�A�f�ʂ̏����ނ��Ƃ��ł��܂��B
���������s�����ׂ�A�f�ʂ̏����ނ��Ƃ��ł��܂��B
�܂�A�ɑ�����_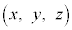 ���������s�������l���܂�(�s�����̕\���̈����Q��)�B
���������s�������l���܂�(�s�����̕\���̈����Q��)�B
x�������Ƃ��锼�a2�̉~�����̓_�́Ax���W�ɂ�����炸�A
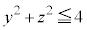 �@����@
�@����@
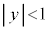 ����
����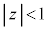 �@����A
�@����A
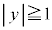 �܂���
�܂���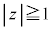 �@����B
�@����B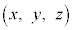 ���������s�����́A�@���B�Ƃ������ƂɂȂ�܂��B
���������s�����́A�@���B�Ƃ������ƂɂȂ�܂��B
A��x���̂܂���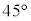 ��]����ƁA�@�͕ς��Ȃ��Ayz���ʏ�ŕs�����B�̋��E��
��]����ƁA�@�͕ς��Ȃ��Ayz���ʏ�ŕs�����B�̋��E��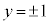 �C
�C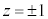 ���ǂ��Ȃ邩���l����ƁA����
���ǂ��Ȃ邩���l����ƁA����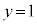 �́A����
�́A����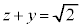 �Ɉڂ�A����
�Ɉڂ�A����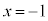 �́A����
�́A����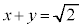 �Ɉڂ�A����
�Ɉڂ�A����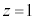 �́A����
�́A����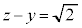 �Ɉڂ�A����
�Ɉڂ�A����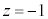 �́A����
�́A����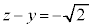 �Ɉڂ�܂��B���̌��ʇB���\���̈�́A
�Ɉڂ�܂��B���̌��ʇB���\���̈�́A
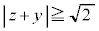 �܂���
�܂���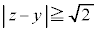 �@����C
�@����C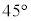 ��]����ƁA�@���C���\���̈�Ɉڂ�܂��B
��]����ƁA�@���C���\���̈�Ɉڂ�܂��B
����ɁAz���̂܂���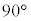 ��](���f�����ʏ�̉�]���Q��)����Ƃ��Axy���ʏ�œ_
��](���f�����ʏ�̉�]���Q��)����Ƃ��Axy���ʏ�œ_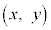 ��
��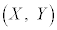 �Ɉڂ�Ƃ��āA
�Ɉڂ�Ƃ��āA
���A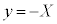 �C
�C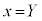
������@�ɑ������ƁA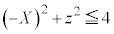 �C
�C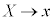 �Ƃ��āA
�Ƃ��āA
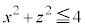 �@����D
�@����D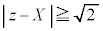 �C
�C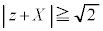 �C
�C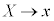 �Ƃ��āA
�Ƃ��āA
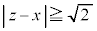 �܂���
�܂���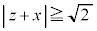 �@����E
�@����E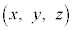 ���������s�����́A�D���E�Ƃ������ƂɂȂ�܂��B
���������s�����́A�D���E�Ƃ������ƂɂȂ�܂��B
�ȏ���AA��B�̋��ʕ����ɂ���_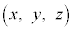 ���������s�����́A�u�@���B�v���u�D���E�v�A�܂�A
���������s�����́A�u�@���B�v���u�D���E�v�A�܂�A
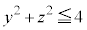 ���u
���u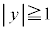 �܂���
�܂���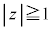 �v����
�v����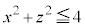 ���u
���u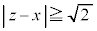 �܂���
�܂���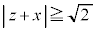 �v�@����F
�v�@����F
A��B�̋��ʕ�����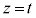 �Ő����f�ʂ��l���܂��B�F�ɂ����āA
�Ő����f�ʂ��l���܂��B�F�ɂ����āA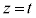 �Ƃ��āA
�Ƃ��āA
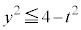 ���u
���u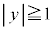 �܂���
�܂���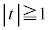 �v����
�v����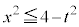 ���u
���u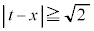 �܂���
�܂���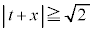 �v�@����G
�v�@����G
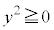 �C
�C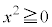 ���A
���A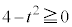 �ł����āA
�ł����āA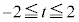 �ł��BA��B�̋��ʕ����́A
�ł��BA��B�̋��ʕ����́A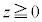 �̕�����
�̕�����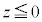 �̕����Ƃœ����`�ɂȂ�̂ŁAA��B�̋��ʕ����̑̐ς́A
�̕����Ƃœ����`�ɂȂ�̂ŁAA��B�̋��ʕ����̑̐ς́A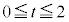 �̕����̑̐ς�2�{���ċ��߂܂��B
�̕����̑̐ς�2�{���ċ��߂܂��B
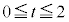 �Ƃ��ćG�����Ē��ׂ�ƁA�ȉ��̂悤�ɂȂ�܂��B
�Ƃ��ćG�����Ē��ׂ�ƁA�ȉ��̂悤�ɂȂ�܂��B
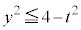 ���A
���A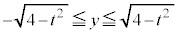 �@����H
�@����H
�u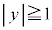 �܂���
�܂���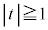 �v���A
�v���A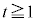 �ł����y�͔C�ӂŁA
�ł����y�͔C�ӂŁA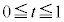 �ł����
�ł����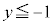 �܂���
�܂���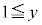 �@����I
�@����I
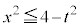 ���A
���A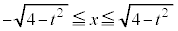 �@����J
�@����J
�u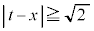 �܂���
�܂���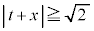 �v���A
�v���A
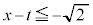 �܂���
�܂���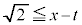 �܂���
�܂���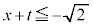 �܂���
�܂���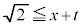 �@����K
�@����K
�܂�A
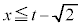 �܂���
�܂���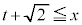 �܂���
�܂���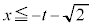 �܂���
�܂���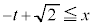
�����ŁA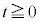 �ł���A
�ł���A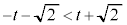 �͖��炩�ł����A
�͖��炩�ł����A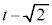 ��
��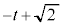 �̑召�W�����ɂȂ�܂��B�����Ƃ�ƁA
�̑召�W�����ɂȂ�܂��B�����Ƃ�ƁA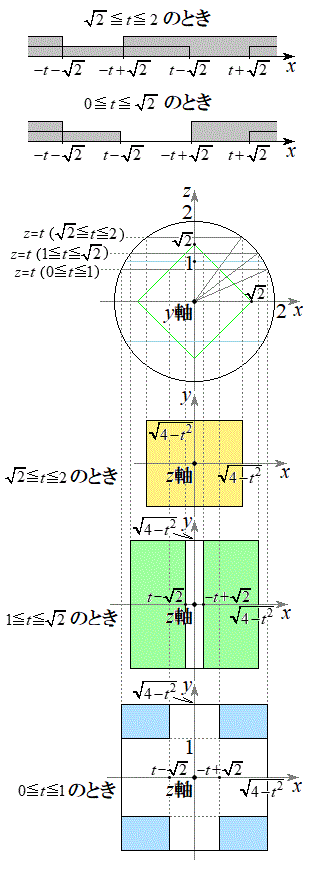 ����ćK�́A�E�}�̂悤�ɁA
����ćK�́A�E�}�̂悤�ɁA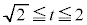 �̂Ƃ��A
�̂Ƃ��A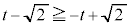 �ƂȂ�Ax�͔C�ӁB
�ƂȂ�Ax�͔C�ӁB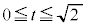 �̂Ƃ��A
�̂Ƃ��A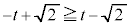 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA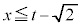 �܂���
�܂���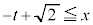 �@����L
�@����L
�܂��A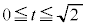 �ɂ�����J��
�ɂ�����J�� �ƇL��
�ƇL��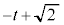 �Ƃ̑召�W�ׂĂ����ƁA
�Ƃ̑召�W�ׂĂ����ƁA
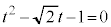 �̉���
�̉���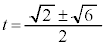 �C
�C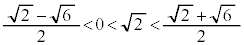 �Ȃ̂ŁA�㎮�E�ӂ̕��q�͐��ŁA
�Ȃ̂ŁA�㎮�E�ӂ̕��q�͐��ŁA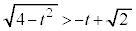
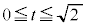 �ɂ�����H��
�ɂ�����H��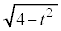 �ƇI��1�Ƃ̑召�W�́A
�ƇI��1�Ƃ̑召�W�́A
���A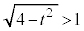
�ȏ���At �ɂ��ďꍇ��������ƁA�G���Ȃ킿�A�H���I���J���L�́A
�E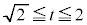 �̂Ƃ��Ax�Cy�͔C�ӁA���A
�̂Ƃ��Ax�Cy�͔C�ӁA���A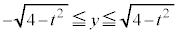 �C����
�C����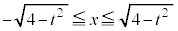
����āA����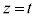 ���
���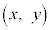 �̑��ݔ͈͂́A�E�}�̔����F���F���B
�̑��ݔ͈͂́A�E�}�̔����F���F���B �E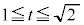 �̂Ƃ��A
�̂Ƃ��A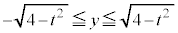 �C���Ay�͔C�ӁA���A�u
�C���Ay�͔C�ӁA���A�u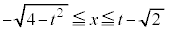 �܂���
�܂���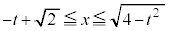 �v
�v ����āA����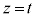 ���
���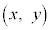 �̑��ݔ͈͂́A�E�}�̔��ΐF���F���B
�̑��ݔ͈͂́A�E�}�̔��ΐF���F���B �E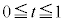 �̂Ƃ��A
�̂Ƃ��A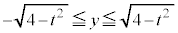 �C���A�u
�C���A�u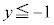 �܂���
�܂���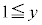 �v�C����
�v�C����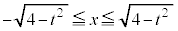 �C���A�u
�C���A�u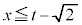 �܂���
�܂���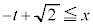 �v
�v ����āA����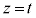 ���
���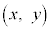 �̑��ݔ͈͂́A�E�}�̔����F���F���B
�̑��ݔ͈͂́A�E�}�̔����F���F���B
����āAA��B�̋��L������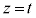 (
(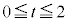 )�Ő����Ƃ��̒f�ʐ�
)�Ő����Ƃ��̒f�ʐ�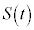 �́A
�́A
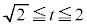 �̂Ƃ��A
�̂Ƃ��A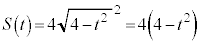
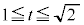 �̂Ƃ��A
�̂Ƃ��A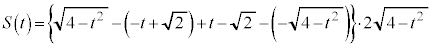
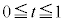 �̂Ƃ��A
�̂Ƃ��A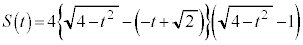
���߂��̐���(��ϕ����������Ƃ���͐ϕ���Ԃ��Ȃ��Čv�Z���܂��B��ϕ����Q��)�A
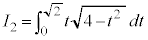 �́A
�́A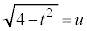 �Ƃ�����(�u���ϕ����Q��)�A
�Ƃ�����(�u���ϕ����Q��)�A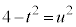 �C
�C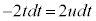 �C
�C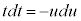 �Ct�F
�Ct�F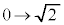 �̂Ƃ��Au�F
�̂Ƃ��Au�F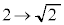 ���A
���A
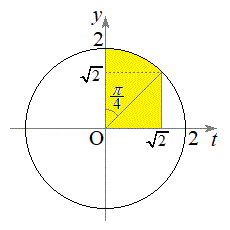
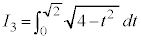 �́A�E�}���F���F���̂悤�ɁA���a2�̉~��
�́A�E�}���F���F���̂悤�ɁA���a2�̉~��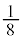 �ƁA���
�ƁA���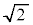 ����
����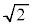 �̎O�p�`�̖ʐς̘a��(�u���ϕ�(����2)���Q��)�A
�̎O�p�`�̖ʐς̘a��(�u���ϕ�(����2)���Q��)�A
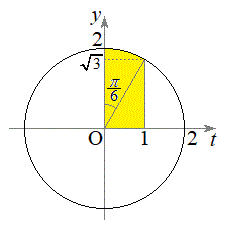
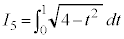 �́A�E�}���F���F���̂悤�ɁA���a2�̉~��
�́A�E�}���F���F���̂悤�ɁA���a2�̉~��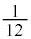 �ƁA���1����
�ƁA���1����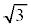 �̎O�p�`�̖ʐς̘a�ŁA
�̎O�p�`�̖ʐς̘a�ŁA
����āA
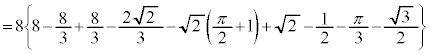
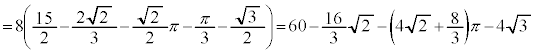 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 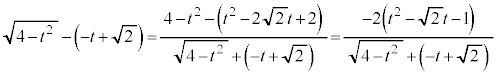
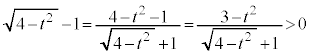
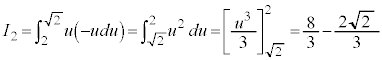
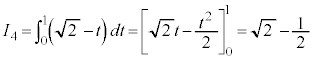
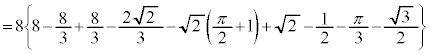
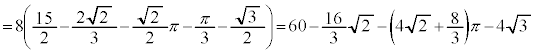 ......[��]
......[��]