���嗝�n���w'08�N�O��[6]
���W���ʂɂ����āA�}��ϐ�t��p����
�@�@�@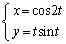 �@�@(
�@�@(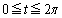 )
)
�ƕ\�����Ȑ����͂ޗ̈�̖ʐς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�O���t��`���A�Ƃ�����肾�Ƃ��Ă��[���ɂ������낢���ł����A�����ł́A�ʐς����Ă��邾���Ȃ̂ŁA�������đ����\�ׂ��肷��ƁA�傫�����Ԃ����X����̂Œ��ӂ��Ă��������B�ʐς����߂�̂ɕK�v�ȏ��邱�Ƃ�D�悷��ׂ��ł��B
���̖��̉Ƃ��Ă͕s�K�v�ł����A�ꉞ�A�������m�F���Ă����܂��B
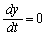 �Ƃ���ƁA
�Ƃ���ƁA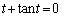 �ƂȂ�܂����A
�ƂȂ�܂����A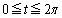 �ɂ����ẮA
�ɂ����ẮA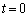 �ƁA
�ƁA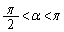 �C
�C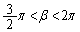 ����α�Cβ �ɂ��āA
����α�Cβ �ɂ��āA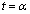 �C
�C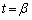 ��3���������Ă��܂��B
��3���������Ă��܂��B
���ǁA�����ׂĂ��A�O���t�͕`���܂���B������A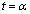 �C
�C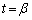 �̂Ƃ���y���W�Ȃǒ��o���A�ǂ�ǂԂ����X���邱�ƂɂȂ�܂��B
�̂Ƃ���y���W�Ȃǒ��o���A�ǂ�ǂԂ����X���邱�ƂɂȂ�܂��B
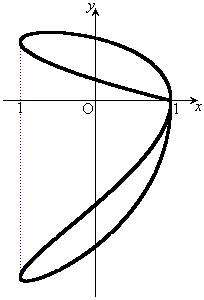 ���́A�O���t�͉E�}�̂悤�ɂȂ�܂��B
���́A�O���t�͉E�}�̂悤�ɂȂ�܂��B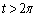 �ł́A�ǂ�ǂ�A�㉺�ɗt���A�Ȃ��Ă��������ɂȂ�܂��B
�ł́A�ǂ�ǂ�A�㉺�ɗt���A�Ȃ��Ă��������ɂȂ�܂��B
�����ł́A�O���t��`�����ƂȂ��l���邱�Ƃɂ��܂��B�܂��A�Ȑ����͂ޗ̈�ɂ��Ē��ׂ܂��B
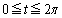 �@����@
�@����@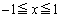 �ł��B
�ł��B
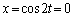 �Ƃ���ƁA�@�ɂ����ẮA
�Ƃ���ƁA�@�ɂ����ẮA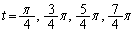
���̂Ƃ��A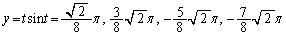
�Ȑ��́Ay���ƁA4�_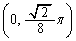 �C
�C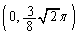 �C
�C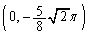 �C
�C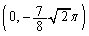 �Ō����܂��B
�Ō����܂��B
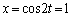 �Ƃ���ƁA�@�ɂ����ẮA
�Ƃ���ƁA�@�ɂ����ẮA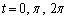
����3��t�̒l�ɑ��āA��������A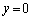
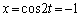 �Ƃ���ƁA�@�ɂ����ẮA
�Ƃ���ƁA�@�ɂ����ẮA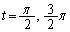
���̂Ƃ��A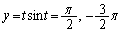
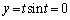 �Ƃ���ƁA�@�ɂ����ẮA
�Ƃ���ƁA�@�ɂ����ẮA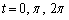 �ŁA
�ŁA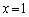
����ŁA�O���t�͇@�͈̔͂ɂ����ď��Ȃ��Ƃ�4�{�Ɏ}�����ꂵ�āA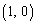 ��1�_�ɏW�܂��Ă��邱�ƁAx���Ƃ�
��1�_�ɏW�܂��Ă��邱�ƁAx���Ƃ�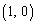 �ȊO�̌�_�������Ȃ����ƁA
�ȊO�̌�_�������Ȃ����ƁA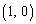 �Ƌt����
�Ƌt����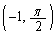 �C
�C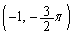 �ɂ����āA4�{�̂�����2�{����1�_�ɏW�܂邱�Ƃ��킩��܂��B
�ɂ����āA4�{�̂�����2�{����1�_�ɏW�܂邱�Ƃ��킩��܂��B
�@�͈̔͂ɂ����āA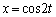 �́A
�́A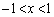 �͈̔͂�2��������̂ŁA�O���t��4�{�Ɏ}�����ꂵ�܂��B4�{�̎}�́A�@�͈̔͂��āA
�͈̔͂�2��������̂ŁA�O���t��4�{�Ɏ}�����ꂵ�܂��B4�{�̎}�́A�@�͈̔͂��āA
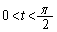 �@����A
�@����A
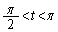 �@����B
�@����B
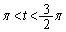 �@����C
�@����C
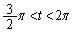 �@����D
�@����D
�����x���W�ɂ�����y�̒l���r���邱�ƂɂȂ�̂ŁA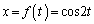 �C
�C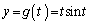 �Ƃ��A�A�C�B�C�C�C�D�ɂ�����y���W���A
�Ƃ��A�A�C�B�C�C�C�D�ɂ�����y���W���A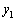 �C
�C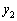 �C
�C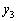 �C
�C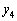 �Ƃ��܂��B
�Ƃ��܂��B
�A�C�B�ɂ�����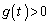 ���A
���A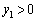 �C
�C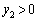
�C�C�D�ɂ�����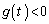 ���A
���A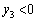 �C
�C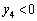
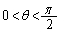 �Ƃ��āA
�Ƃ��āA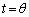 �͇A�C
�͇A�C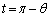 �͇B���A
�͇B���A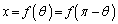 �ɂ�����y���W���r����ƁA
�ɂ�����y���W���r����ƁA
�� 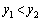
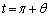 �͇C�C
�͇C�C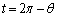 �͇D���A
�͇D���A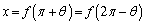 �ɂ�����y���W���r����ƁA
�ɂ�����y���W���r����ƁA
�� 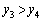
�]���āA�A�C�B�C�C�C�D��4�{�́A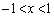 �ɂ����Č��������A�ォ��A
�ɂ����Č��������A�ォ��A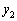 �C
�C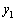 �C
�C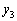 �C
�C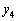 �̏��ɕ��сA�Ȑ����͂ޕ����́A
�̏��ɕ��сA�Ȑ����͂ޕ����́A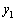 ��
��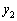 ���͂ޕ����A
���͂ޕ����A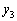 ��
��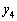 ���͂ޕ�����2���邱�Ƃ��킩��܂��B�������ăO���t��`���A�Ƃ������Ƃ������Ƃ��A����ŁA�ʐς����߂�̂ɂ͏[���ł��B
���͂ޕ�����2���邱�Ƃ��킩��܂��B�������ăO���t��`���A�Ƃ������Ƃ������Ƃ��A����ŁA�ʐς����߂�̂ɂ͏[���ł��B
�ʐς����߂�ɂ������āA4�{�̎}�̊e�͈͇A�`�D�ɗ��[���܂߂čl���邱�Ƃɂ��܂��B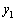 �C
�C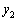 �C
�C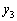 �C
�C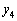 ���A
���A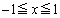 �ɂ�����x���ƈ͂ޖʐς�
�ɂ�����x���ƈ͂ޖʐς�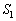 �C
�C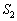 �C
�C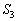 �C
�C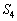 �Ƃ��܂��B���߂�ʐ�S�́A
�Ƃ��܂��B���߂�ʐ�S�́A
�ł��B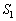 �ł́A
�ł́A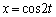 �ƒu�����邱�Ƃɂ��Ax�F
�ƒu�����邱�Ƃɂ��Ax�F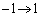 �̂Ƃ��At�F
�̂Ƃ��At�F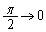 ���A
���A
�����悤�Ȑϕ����o�Ă���̂ŁA
�Ƃ����ƁA
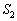 �ł́Ax�F
�ł́Ax�F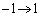 �̂Ƃ��At�F
�̂Ƃ��At�F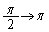 ���A
���A
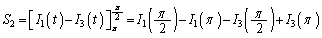
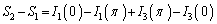 �@(
�@(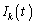 �̒���sin�̍��̓[���ƂȂ�Acos�̂ݎc�邱�Ƃɒ��ӂ��Ă�������)
�̒���sin�̍��̓[���ƂȂ�Acos�̂ݎc�邱�Ƃɒ��ӂ��Ă�������)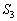 �C
�C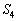 �ł́A���ꂼ��Ax�F
�ł́A���ꂼ��Ax�F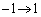 �̂Ƃ��At�F
�̂Ƃ��At�F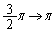 �Ct�F
�Ct�F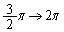 �ł����A
�ł����A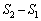 �Ɠ��l�ɁA
�Ɠ��l�ɁA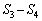 �ɂ����Ă��A
�ɂ����Ă��A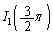 �C
�C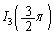 �͏����āA
�͏����āA
�� 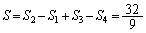 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B