�d����e���\��
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�����@���͑S�Ă̍��W�n�ɂ����ċ��ςł���ׂ��A�Ƃ����A�C���V���^�C���ɂ�鑊�ΐ��̗v��(�v�ʃe���\�����Q��)�ɂ��A�}�N�X�E�F���̕����������W�ϊ��ɑ��ċ��ςł���ׂ��ł��B���ςł��邩�ǂ����ׂ邽�߂ɁA�}�N�X�E�F���̕��������e���\����p���ĕ\�����邱�Ƃ��l���܂��B
��ԓ��̊e�_�ɂ����āA�d�E��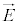 �C���E��
�C���E��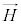 �C�U�d����ε�C��������μ�Ƃ��āA�d�����x��
�C�U�d����ε�C��������μ�Ƃ��āA�d�����x��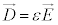 �C�������x��
�C�������x��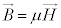 �C�܂��A�d�ז��x��ρ�C�d�����x��
�C�܂��A�d�ז��x��ρ�C�d�����x��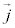 �Ƃ��āA
�Ƃ��āA
�}�N�X�E�G���̕������F
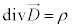 �@����@�@
�@����@�@
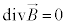 �@����A�@
�@����A�@
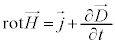 �@����B�@
�@����B�@
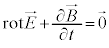 �@����C�@
�@����C�@
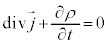 �@����D
�@����D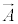 ������E
������E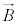 �C�d�E
�C�d�E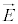 �����߂鎮�A
�����߂鎮�A
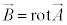 �C
�C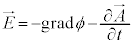 �@�E
�@�E
�K���Ȋ�χ��p�����Q�[�W�ϊ��F
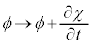 �C
�C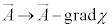 �@����F
�@����F
�x�N�g���E�|�e���V����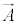 ���g�����Aϕ���܂߂āA4���x�N�g��
���g�����Aϕ���܂߂āA4���x�N�g��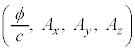 ���l���܂��B������A
���l���܂��B������A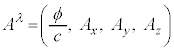 �Ə����A4���x�N�g���E�|�e���V�����ƌ����܂��Bλ�́A
�Ə����A4���x�N�g���E�|�e���V�����ƌ����܂��Bλ�́A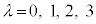 ��\���A
��\���A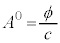 �C
�C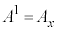 �C
�C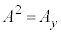 �C
�C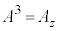 �ł��B
�ł��B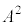 �C
�C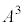 ��A��2��A3��Ƃ����Ӗ��ł͂Ȃ��A
��A��2��A3��Ƃ����Ӗ��ł͂Ȃ��A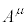 �̑�2�����A��3�����Ƃ����Ӗ��ł��B
�̑�2�����A��3�����Ƃ����Ӗ��ł��B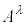 �����σx�N�g���ł��B����ɑ��āA�v�ʃe���\��
�����σx�N�g���ł��B����ɑ��āA�v�ʃe���\��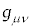 ��p���āA���σx�N�g��
��p���āA���σx�N�g��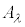 ��
��
�Ƃ��Ē�߂܂��B���[�����c�ϊ��ɂ���č��W�ϊ����s���~���R�t�X�L�[�����ɂ����ẮA�v�ʃe���\��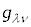 �́A
�́A
�ł��B
�����ŁA�Δ���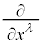 ��
��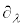 �Ə����A4���x�N�g���|�e���V����
�Ə����A4���x�N�g���|�e���V����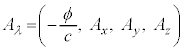 ��p���āA�d����e���\���F
��p���āA�d����e���\���F
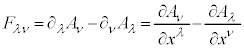 �@����G
�@����G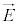 �C���E
�C���E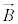 �́A
�́A
�G���A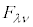 �͓Y��λ�Cν�̓���ւ��ɑ��āA���Ώ�(
�͓Y��λ�Cν�̓���ւ��ɑ��āA���Ώ�(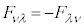 )�Ȃ̂ŁA
)�Ȃ̂ŁA
�ƂȂ�܂��B
�}�N�X�E�F���̕������̇A�ƇC�́A
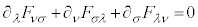 �@����H
�@����H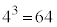 �ʂ�̎���\���悤�Ɍ����܂����Aλ�Cν�Cσ�̂����ɓ��������̂�����ƁA�Ⴆ�A
�ʂ�̎���\���悤�Ɍ����܂����Aλ�Cν�Cσ�̂����ɓ��������̂�����ƁA�Ⴆ�A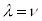 ���Ƃ���ƁA
���Ƃ���ƁA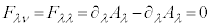 �ł���A�܂��A
�ł���A�܂��A
�ł����āA�H�̍��ӂ͍P���I��0�ł�(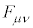 �����Ώ̃e���\��������ł�)�B�H�̍��ӂňӖ�������̂́Aλ�Cν�Cσ�����قȂ�Ƃ������ł��B�H��λ�Cν�Cσ�ɂ��đΏ̂Ȃ̂ŁAλ�Cν�Cσ���z�I����ւ�������͓̂������ɂȂ�܂��B����āA�H�́A�����I��
�����Ώ̃e���\��������ł�)�B�H�̍��ӂňӖ�������̂́Aλ�Cν�Cσ�����قȂ�Ƃ������ł��B�H��λ�Cν�Cσ�ɂ��đΏ̂Ȃ̂ŁAλ�Cν�Cσ���z�I����ւ�������͓̂������ɂȂ�܂��B����āA�H�́A�����I��
��4�ʂ�̏ꍇ�ɈقȂ�������ɂȂ�܂��B�H�́A���ꂼ��A
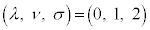 �̂Ƃ��A
�̂Ƃ��A
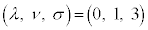 �̂Ƃ��A
�̂Ƃ��A
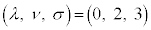 �̂Ƃ��A
�̂Ƃ��A
����3�̎��Ń}�N�X�E�F���̕������̇C��^���܂��B
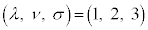 �̂Ƃ��A
�̂Ƃ��A
����́A�}�N�X�E�F���̕������̇A�ł��B
�d�ז��x��ρ�C�d���x�N�g����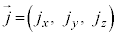 �Ƃ��āA4���d�����x��
�Ƃ��āA4���d�����x��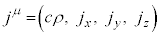 �Ƃ��A���σe���\��
�Ƃ��A���σe���\��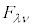 ���甽�σe���\��
���甽�σe���\��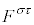 ���A
���A
�Ƃ��č��܂��B�Ⴆ�A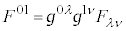 �ł����āA
�ł����āA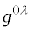 ��
��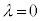 �̂Ƃ��̂�
�̂Ƃ��̂�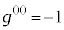 �C
�C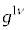 ��
��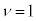 �̂Ƃ��̂�
�̂Ƃ��̂�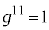 �ŁA
�ŁA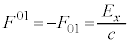 �C
�C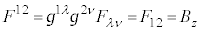 �̂悤�ɂȂ��Ă��܂��B
�̂悤�ɂȂ��Ă��܂��B
�����p���āA�}�N�X�E�F���̕������̇@�ƇB�́A
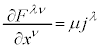 �@����I
�@����I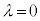 �̂Ƃ��A�I�́A
�̂Ƃ��A�I�́A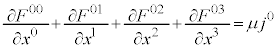
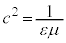 ���A
���A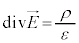 �C����̓}�N�X�E�F���̕������̇@�ł��B
�C����̓}�N�X�E�F���̕������̇@�ł��B
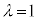 �̂Ƃ��A�I�́A
�̂Ƃ��A�I�́A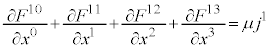
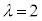 �̂Ƃ��A�I�́A
�̂Ƃ��A�I�́A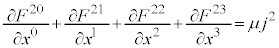
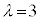 �̂Ƃ��A�I�́A
�̂Ƃ��A�I�́A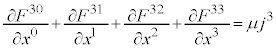
�ȏ��3�������킹�āA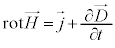 �C����̓}�N�X�E�F���̕������̇B�ł��B
�C����̓}�N�X�E�F���̕������̇B�ł��B
�ȏ���A�}�N�X�E�F���̕������@�`�C�́A����2���ɂ܂Ƃ߂��܂��B
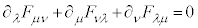 �@����H
�@����H
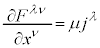 �@����I
�@����I
�d���ۑ��̎��F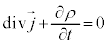 �́A4���x�N�g���ŏ����ƁA
�́A4���x�N�g���ŏ����ƁA
�����A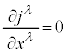 �@����J�@�Ƃ����`�ɂȂ�܂��B
�@����J�@�Ƃ����`�ɂȂ�܂��B
�I��p���Ă��A���ӂ�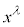 �Ŕ�����λ�ɂ��Ęa���Ƃ�ƁA
�Ŕ�����λ�ɂ��Ęa���Ƃ�ƁA
���̉E�ӂ́Aλ�Cν�ɂ��đΏ̂Ȍ`�����Ă���A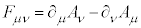 �C�܂��A
�C�܂��A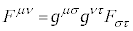 �����Ώ̃e���\���ł��邱�Ƃ��l����ƁA0�ɂȂ�܂��B�܂�A�J�͇I����������܂��B
�����Ώ̃e���\���ł��邱�Ƃ��l����ƁA0�ɂȂ�܂��B�܂�A�J�͇I����������܂��B
�}�N�X�E�F���̕������H�C�I�����[�����c�ϊ�����Ƃǂ��Ȃ邩���l���܂��BK�n�̍��W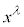 ��
�� �n�̍��W
�n�̍��W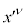 �̃��[�����c�ϊ���\���e���\��
�̃��[�����c�ϊ���\���e���\��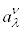 ���A
���A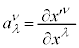 �̂悤�Ɍ���ƁAK�n�̓d����e���\��
�̂悤�Ɍ���ƁAK�n�̓d����e���\��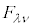 �Ƀ��[�����c�ϊ����s���ƁA
�Ƀ��[�����c�ϊ����s���ƁA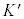 �n�ł́A
�n�ł́A
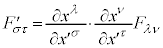 �@����K
�@����K
�K�̗��ӂ�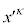 �Ŕ�������ƁA
�Ŕ�������ƁA
���[�����c�ϊ��ł́A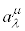 ���t�ϊ���
���t�ϊ���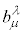 ���e�����́A
���e�����́A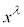 �C
�C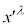 ��1�������A�������͒萔�Ȃ̂ŁA
��1�������A�������͒萔�Ȃ̂ŁA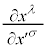 �C
�C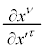 �͒萔�ŁA
�͒萔�ŁA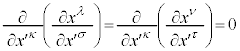 �ł��B����āA
�ł��B����āA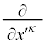 ��
��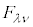 �݂̂ɓ����A�A���藝���g���āA
�݂̂ɓ����A�A���藝���g���āA
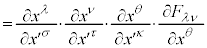 �@����L
�@����L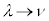 �C
�C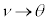 �C
�C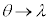 �C
�C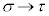 �C
�C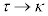 �C
�C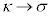 �Ƃ���ƁA
�Ƃ���ƁA
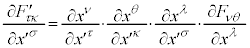 �@����M
�@����M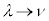 �C
�C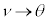 �C
�C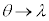 �C
�C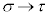 �C
�C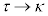 �C
�C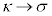 �Ƃ���ƁA
�Ƃ���ƁA
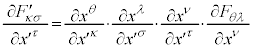 �@����N
�@����N
����āA�H�F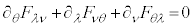 �ł���A
�ł���A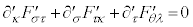 �ł����āA�H�́A���[�����c�ϊ������Ă��`��ς��܂���B
�ł����āA�H�́A���[�����c�ϊ������Ă��`��ς��܂���B
K�n���d�����x�x�N�g��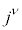 �̓��[�����c�ϊ��ɂ��A
�̓��[�����c�ϊ��ɂ��A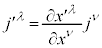 �ɕϊ�����A�d����e���\��
�ɕϊ�����A�d����e���\��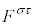 �́A���[�����c�ϊ��ɂ��A
�́A���[�����c�ϊ��ɂ��A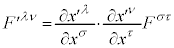 �ɕϊ�����܂��B�����
�ɕϊ�����܂��B�����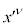 �Ŕ�������ƁA
�Ŕ�������ƁA
�I���A���[�����c�ϊ��ɂ��`��ς��Ȃ����Ƃ��킩��܂��B
�܂�A�}�N�X�E�F���̕������́A���[�����c�ϊ��ɂ��`��ς��Ȃ����Ƃ��킩��܂��B�����d���g���`�d���x�����^������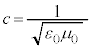 �͂ǂ̍��W�n�ɂ����Ă��ς��Ȃ��A�Ƃ������Ƃł��B
�͂ǂ̍��W�n�ɂ����Ă��ς��Ȃ��A�Ƃ������Ƃł��B
���[�����c�E�Q�[�W�F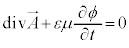 ����
����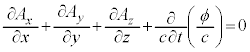 �́A4���|�e���V����
�́A4���|�e���V����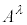 ��p����
��p����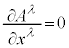 �ƕ\����̂ŁA���[�����c�ϊ��ɂ��`��ς��܂���B���[�����c�E�Q�[�W��I�ꍇ�̃|�e���V����ϕ�C
�ƕ\����̂ŁA���[�����c�ϊ��ɂ��`��ς��܂���B���[�����c�E�Q�[�W��I�ꍇ�̃|�e���V����ϕ�C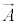 ���������ׂ��������́A
���������ׂ��������́A
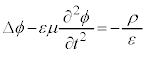 �@����O
�@����O
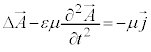 �@����P
�@����P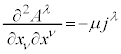 �ƕ\�����̂ŁA��͂胍�[�����c�ϊ��ɂ��`��ς��܂���B
�ƕ\�����̂ŁA��͂胍�[�����c�ϊ��ɂ��`��ς��܂���B
���D�N�[�����E�Q�[�W�́A�e���\���`���ŕ\���ł����A���[�����c�ϊ����{���ƌ`��ς��Ă��܂��܂��B
�ȏ�̗�������Ă���ƁA�����@�����e���\�����g���ĕ\���ł���A���[�����c�ϊ��ɑ��ċ��ςł���A�Ƃ������Ƃ����������ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 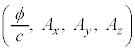 ���l���܂��B������A
���l���܂��B������A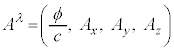 �Ə����A4���x�N�g���E�|�e���V�����ƌ����܂��Bλ�́A
�Ə����A4���x�N�g���E�|�e���V�����ƌ����܂��Bλ�́A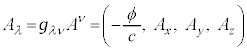
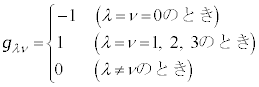
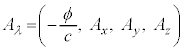 ��p���āA�d����e���\���F
��p���āA�d����e���\���F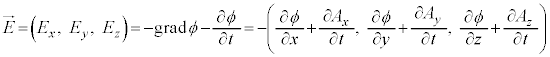
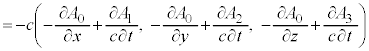
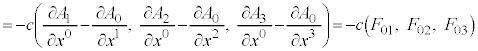
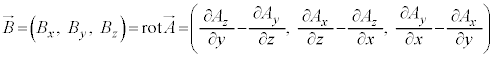
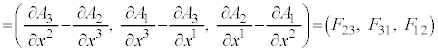

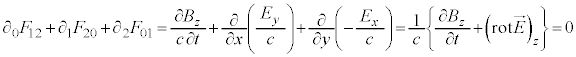
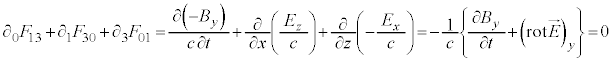
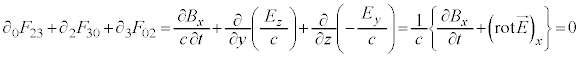
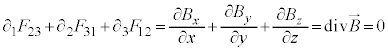
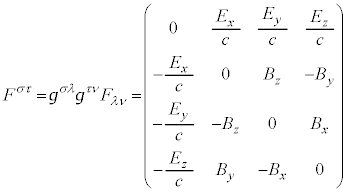
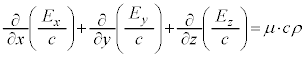
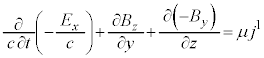
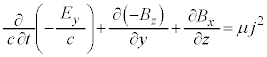
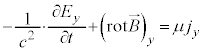 �C�܂�A
�C�܂�A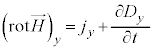

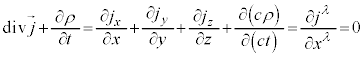
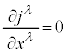 �@����J�@�Ƃ����`�ɂȂ�܂��B
�@����J�@�Ƃ����`�ɂȂ�܂��B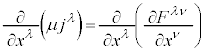
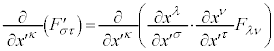
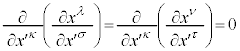 �ł��B����āA
�ł��B����āA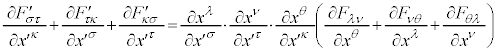
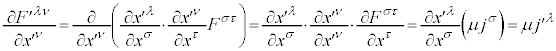
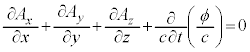 �́A4���|�e���V����
�́A4���|�e���V����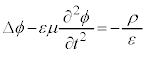 �@����O
�@����O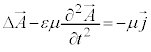 �@����P
�@����P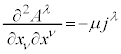 �ƕ\�����̂ŁA��͂胍�[�����c�ϊ��ɂ��`��ς��܂���B
�ƕ\�����̂ŁA��͂胍�[�����c�ϊ��ɂ��`��ς��܂���B