��啨��'24�N�O��[1]
�����ȏ��̏��x���ɉ����ĉ^�����鏬����P��Q�ɂ��čl����B���̏����̓��m�̏Փ˂͒e���Փ˂Ƃ���B�����2�̏����̂́A�L�т邱�Ƃ̂Ȃ����� �̂Ђ��łȂ���Ă���B�Ђ����ɂ�ł���Ƃ��ɂ́A�Ђ��������̂̉^����W���邱�Ƃ͂Ȃ����A�����̊Ԃ̋�����
�̂Ђ��łȂ���Ă���B�Ђ����ɂ�ł���Ƃ��ɂ́A�Ђ��������̂̉^����W���邱�Ƃ͂Ȃ����A�����̊Ԃ̋����� �ɂȂ�ƂЂ��������āA�����̂̊Ԃɂ͂Ђ�����ďu�ԓI�ȗ�(����)���͂��炭�B���̂Ƃ��A�Ђ�������O��ɂ�����2�̏����̂ɂ͗͊w�I�G�l���M�[�ۑ�������щ^���ʕۑ���������������̂Ƃ���B�Ȃ��A�Ђ�����ė͂��y�ڂ��������Ƃ͏Փ˂Ƃ͂�Ȃ��B�܂��A�����̂̑傫���͖����ł���قǏ������A�Ђ��̎��ʂ͖����ł���B�f�肪�Ȃ�����͏��Ə����̂̊Ԃ̖��C�������ł���B�d�͉����x�̑傫����
�ɂȂ�ƂЂ��������āA�����̂̊Ԃɂ͂Ђ�����ďu�ԓI�ȗ�(����)���͂��炭�B���̂Ƃ��A�Ђ�������O��ɂ�����2�̏����̂ɂ͗͊w�I�G�l���M�[�ۑ�������щ^���ʕۑ���������������̂Ƃ���B�Ȃ��A�Ђ�����ė͂��y�ڂ��������Ƃ͏Փ˂Ƃ͂�Ȃ��B�܂��A�����̂̑傫���͖����ł���قǏ������A�Ђ��̎��ʂ͖����ł���B�f�肪�Ȃ�����͏��Ə����̂̊Ԃ̖��C�������ł���B�d�͉����x�̑傫���� �ł���B���x�̐��̌�����x���̐��̌����Ƃ���B
�ł���B���x�̐��̌�����x���̐��̌����Ƃ���B
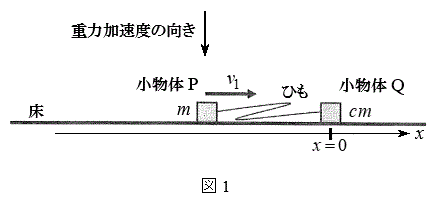 �T�D������P�̎��ʂ�m�C������Q�̎��ʂ�
�T�D������P�̎��ʂ�m�C������Q�̎��ʂ�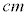 (c�͐��̒萔)�Ƃ���B�}1�̂悤�ɁA
(c�͐��̒萔)�Ƃ���B�}1�̂悤�ɁA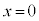 �ŐÎ~���Ă��鏬����Q�ɏ�����P�x
�ŐÎ~���Ă��鏬����Q�ɏ�����P�x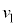 (
(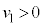 )�ŏՓ˂������B�������A���̍ŏ��̏Փ˂̎�����
)�ŏՓ˂������B�������A���̍ŏ��̏Փ˂̎�����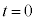 �ł���B
�ł���B
��1�@�ŏ��̏Փ˒���̏�����P��Q�̑��x���Ac�C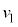 �C
�C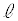 �C
�C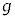 �̂����K�v�Ȃ��̂�p���Ă��ꂼ��\���B
�̂����K�v�Ȃ��̂�p���Ă��ꂼ��\���B ��2�@2�̏����̂͏Փˌ�ɗ���Ă����A�����̊Ԃ̋�����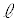 �ƂȂ����Ƃ���łЂ����������B���̒���̏�����P��Q�̑��x���Ac�C
�ƂȂ����Ƃ���łЂ����������B���̒���̏�����P��Q�̑��x���Ac�C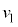 �C
�C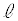 �C
�C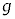 �̂����K�v�Ȃ��̂�p���Ă��ꂼ��\���B
�̂����K�v�Ȃ��̂�p���Ă��ꂼ��\���B ��3�@�Ђ�����������A���炭���ď�����P��Q���ĂяՓ˂����B�A2��ڂ̏Փ˂̎������Ac�C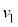 �C
�C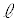 �C
�C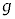 �̂����K�v�Ȃ��̂�p���Ă��ꂼ��\���B
�̂����K�v�Ȃ��̂�p���Ă��ꂼ��\���B ��4�@����t (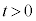 )�ɂ����鏬����P��Q�����킹��2���̂̏d�S�̈ʒu���Ac�C
)�ɂ����鏬����P��Q�����킹��2���̂̏d�S�̈ʒu���Ac�C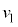 �C
�C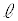 �C
�C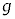 �Ct�@�̂����K�v�Ȃ��̂�p���ĕ\���B
�Ct�@�̂����K�v�Ȃ��̂�p���ĕ\���B
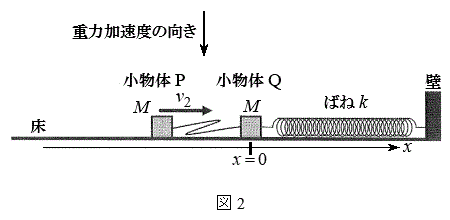 �U�D�}2�̂悤�ɏ�����P��Q�̎��ʂ��Ƃ���M�ł���A������Q���˒萔k�̂˂Ɏ��t�������u���l����B�˂̉E�[�͕ǖʂɌŒ肳��Ă���A�˂̍��[�͏�����Q�Ɨ���邱�Ƃ͂Ȃ��B�͂��߁A������Q��
�U�D�}2�̂悤�ɏ�����P��Q�̎��ʂ��Ƃ���M�ł���A������Q���˒萔k�̂˂Ɏ��t�������u���l����B�˂̉E�[�͕ǖʂɌŒ肳��Ă���A�˂̍��[�͏�����Q�Ɨ���邱�Ƃ͂Ȃ��B�͂��߁A������Q��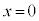 �ŐÎ~���Ă���A�˂͎��R�̒����ł���B���̌�A������P�x
�ŐÎ~���Ă���A�˂͎��R�̒����ł���B���̌�A������P�x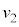 (
(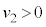 )�ŏ�����Q�Ɍ������ĉ^�������A����
)�ŏ�����Q�Ɍ������ĉ^�������A����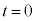 ��1��ڂ̏Փ˂��������B������Q�͏Փˌ�A�˂̗͂��Ȃ���^�������B�������A�˂͏\���ɒ����A�˒萔���\���ɑ傫�����߁A������Q�͕ǂɓ����邱�Ƃ͂Ȃ����̂Ƃ���B
��1��ڂ̏Փ˂��������B������Q�͏Փˌ�A�˂̗͂��Ȃ���^�������B�������A�˂͏\���ɒ����A�˒萔���\���ɑ傫�����߁A������Q�͕ǂɓ����邱�Ƃ͂Ȃ����̂Ƃ���B
��5�@2��ڂ̏Փ˂�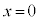 �ŋN���邽�߂ɂ́A�Ђ��̒���
�ŋN���邽�߂ɂ́A�Ђ��̒���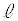 ���A����
���A����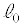 ��蒷���K�v������B�܂��A
��蒷���K�v������B�܂��A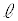 ������
������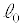 ���Z���ƁA
���Z���ƁA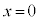 ��2��ڂ̏Փ˂͋N����Ȃ��B����
��2��ڂ̏Փ˂͋N����Ȃ��B����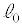 ���AM�C
���AM�C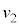 �Ck�C
�Ck�C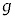 �̂����K�v�Ȃ��̂�p���ĕ\���B
�̂����K�v�Ȃ��̂�p���ĕ\���B 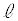 ������
������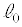 ��蒷���Ƃ��������̂��ƂŁA2��ڈȍ~�̏Փ˂��l����B
��蒷���Ƃ��������̂��ƂŁA2��ڈȍ~�̏Փ˂��l����B
��6�@2��ڂ̏Փ˂̎������AM�C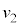 �Ck�C
�Ck�C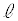 �C
�C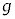 �̂����K�v�Ȃ��̂�p���ĕ\���B
�̂����K�v�Ȃ��̂�p���ĕ\���B ��7�@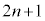 ��ڂ̏Փ˂̎������AM�C
��ڂ̏Փ˂̎������AM�C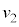 �Ck�C
�Ck�C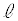 �C
�C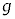 �Cn�̂����K�v�Ȃ��̂�p���ĕ\���B�������An�͐��̐����ł���B
�Cn�̂����K�v�Ȃ��̂�p���ĕ\���B�������An�͐��̐����ł���B
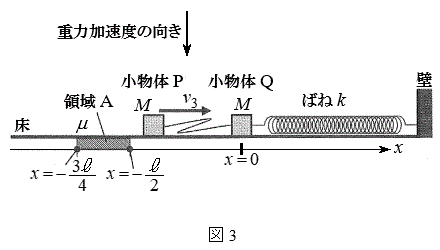 �V�D���ɁA�U�D�ŗp�������u�ɕύX�������A�}3�̂悤��
�V�D���ɁA�U�D�ŗp�������u�ɕύX�������A�}3�̂悤��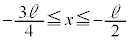 �̗̈�A�݂̂ɂ����ď�����P�Ə��̊Ԃɖ��C�͂��͂��炭�悤�ɂ����B�̈�A�ɂ����鏬����P�Ə��̊Ԃ̓����C�W����μ�Ƃ���B
�̗̈�A�݂̂ɂ����ď�����P�Ə��̊Ԃɖ��C�͂��͂��炭�悤�ɂ����B�̈�A�ɂ����鏬����P�Ə��̊Ԃ̓����C�W����μ�Ƃ���B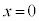 �ŐÎ~���Ă��鏬����Q�ɏ�����P�x
�ŐÎ~���Ă��鏬����Q�ɏ�����P�x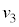 (
(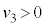 )�ŏՓ˂������Ƃ���A������P��Q��
)�ŏՓ˂������Ƃ���A������P��Q��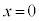 ��2��ڂ̏Փ˂������B���̌�A������P��Q�͂���ɏՓ˂��J��Ԃ��A
��2��ڂ̏Փ˂������B���̌�A������P��Q�͂���ɏՓ˂��J��Ԃ��A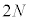 ��ڂ�
��ڂ�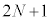 ��ڂ̏Փ˂̊Ԃɏ�����P�͗̈�A�̒��S
��ڂ̏Փ˂̊Ԃɏ�����P�͗̈�A�̒��S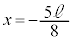 �ŐÎ~�����B�������AN�́A���鐳�̐����ł���B������P��Q���ŏ��ɏՓ˂��Ă���A������P���̈�A�ŐÎ~����܂ł̊ԁA������Q���̈�A�ɓ��邱�Ƃ͂Ȃ������B�܂��A�˂͏\���ɒ����A�˒萔���\���ɑ傫�����߁A������Q�͕ǂɓ����邱�Ƃ͂Ȃ����̂Ƃ���B
�ŐÎ~�����B�������AN�́A���鐳�̐����ł���B������P��Q���ŏ��ɏՓ˂��Ă���A������P���̈�A�ŐÎ~����܂ł̊ԁA������Q���̈�A�ɓ��邱�Ƃ͂Ȃ������B�܂��A�˂͏\���ɒ����A�˒萔���\���ɑ傫�����߁A������Q�͕ǂɓ����邱�Ƃ͂Ȃ����̂Ƃ���B
��8�@��L�̉^������������ɂ́A�����C�W��μ������l���Ƃ�K�v������B���̎�肤�邷�ׂĂ̒l���AM�C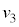 �Ck�C
�Ck�C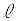 �C
�C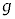 �CN�̂����K�v�Ȃ��̂�p���ĕ\���B
�CN�̂����K�v�Ȃ��̂�p���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�Ђ��łȂ��ꂽ2���̂Ƃ˂Ɋւ�����ł��B��7�C��8�͂��Ȃ��₱�����A���J�ɍl����K�v������܂��B
�T�D��1�@�ŏ��̏Փ˒���̏�����P��Q�̑��x��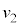 �C
�C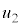 �Ƃ��܂��B�^���ʕۑ����A
�Ƃ��܂��B�^���ʕۑ����A 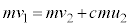 �@����@
�@����@����āA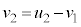 �@����A
�@����A
�@�ɑ������ƁA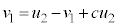
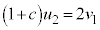 �@��
�@�� 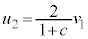
�A�ɑ�����āA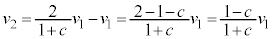
����āA�Փ˒����P�̑��x��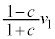 �CQ�̑��x��
�CQ�̑��x��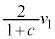 ......[��]
......[��]
��2�@1��ڂ̏Փ˂̌�A2�����͓̂����x�^�����܂��B�Ђ�������������̏�����P�CQ�̑��x��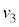 �C
�C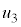 �Ƃ���ƁA�Ђ�������O��̉^���ʕۑ����A
�Ƃ���ƁA�Ђ�������O��̉^���ʕۑ����A 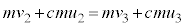 �@����B
�@����B����āA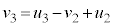 �@����C
�@����C
�B�ɑ������ƁA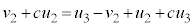
��1�̌��ʂ������āA
�� 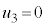 �C�ɑ�����A��1�̌��ʂ�p���āA
�C�ɑ�����A��1�̌��ʂ�p���āA 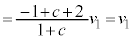 �@����D
�@����D����āA�Ђ��������������P�̑��x��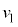 �CQ�̑��x��0 ......[��]
�CQ�̑��x��0 ......[��] ���D���̌��ʂ́A�B�Ɣ����W���̎���A�����ĉ����Ȃ��Ă��A���邢�͇B�Ɨ͊w�I�G�l���M�[�ۑ��̎��������Ȃ��Ă��A�\���ł��܂��B�݂̖̂��Ȃ̂Œ��ӂ��Ă��������B
��3�@�ŏ��̏Փ˂���Ђ�������܂ł̎��Ԃ́A�D��p���āA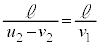 �C�Ђ��������Ă���2��ڂ̏Փ˂܂ł̎��Ԃ́A��2�̌��ʂ�p���āA
�C�Ђ��������Ă���2��ڂ̏Փ˂܂ł̎��Ԃ́A��2�̌��ʂ�p���āA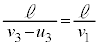 �C����āA2��ڂ̏Փ˂̎����́A
�C����āA2��ڂ̏Փ˂̎����́A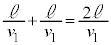 ......[��]
......[��]
��4�@�^���ʂ��ۑ������n�ł́A�����d�S�͓����x�^���𑱂��܂��B�ŏ��̏Փ˂܂ł̏d�S�̑��x��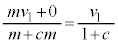 �ł��B�Փˌ���A�Ђ�������������A�d�S�͂��̑��x�ʼn^���𑱂���̂ŁA�d�S�̈ʒu�́A
�ł��B�Փˌ���A�Ђ�������������A�d�S�͂��̑��x�ʼn^���𑱂���̂ŁA�d�S�̈ʒu�́A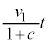 ......[��]
......[��]
�U�D��5�@���ʂ�������2���̂̏Փ˂ł͑��x����������(�ՓˁE���́E����̖�����Q��)�A�Փ˒���̏�����P�CQ�̑��x�́A0�C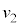 �ł��B�Ђ����[���ɒ�����A������Q���P�U�����āA�˂̍ő�k�݂̈ʒu(�U���[)�ɒB������A���]����
�ł��B�Ђ����[���ɒ�����A������Q���P�U�����āA�˂̍ő�k�݂̈ʒu(�U���[)�ɒB������A���]����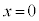 �ɖ߂菬����P�ƏՓ˂��܂��B�Ђ����Z���A������Q���U���[�ɒB����O�ɂЂ��������Ă��܂��ƁA
�ɖ߂菬����P�ƏՓ˂��܂��B�Ђ����Z���A������Q���U���[�ɒB����O�ɂЂ��������Ă��܂��ƁA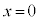 �ŐÎ~���Ă���������P��x���������ɓ����o���Ă��܂����߁A
�ŐÎ~���Ă���������P��x���������ɓ����o���Ă��܂����߁A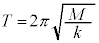 ��2��ڂ̏Փ˂��N����Ȃ��Ȃ�܂��B
��2��ڂ̏Փ˂��N����Ȃ��Ȃ�܂��B ������Q�̒P�U��(�ːU��q���Q��)�́A����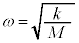 �C�p�U����
�C�p�U����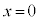 �ł����āA�Փˈʒu
�ł����āA�Փˈʒu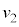 ���U�����S�ł���A�Փ˒���̑���
���U�����S�ł���A�Փ˒���̑���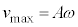 ���P�U���̑����̍ő�l�Ȃ̂ŁA�P�U���̌����F
���P�U���̑����̍ő�l�Ȃ̂ŁA�P�U���̌����F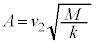 ���A�U��A��
���A�U��A��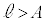 �ł��B
�ł��B
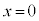 �łȂ����
�łȂ����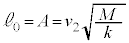 ��2��ڂ̏Փ˂��N����Ȃ��Ȃ�̂ŁA
��2��ڂ̏Փ˂��N����Ȃ��Ȃ�̂ŁA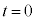 ......[��]
......[��]
��6�@1��ڂ̏Փ�(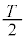 )����2��ڂ̏Փ˂܂ł̎��Ԃ͒P�U���̔�����
)����2��ڂ̏Փ˂܂ł̎��Ԃ͒P�U���̔�����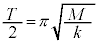 �ł��B2��ڂ̏Փ˂̎����́A
�ł��B2��ڂ̏Փ˂̎����́A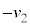 ......[��]
......[��]
��7�@2��ڂ̏Փ˒��O�̏�����Q�̑��x�́A�P�U���̔�������̑��x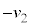 �ł��B2��ڂ̏Փ˂ŁA�ĂсA������P�CQ�ő��x���������A�Փ˒���̏�����P�̑��x��
�ł��B2��ڂ̏Փ˂ŁA�ĂсA������P�CQ�ő��x���������A�Փ˒���̏�����P�̑��x��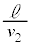 �C������Q�̑��x��0�ł��B�������玞��
�C������Q�̑��x��0�ł��B�������玞��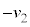 �̌�A�Ђ�������A�T�D�̍l�@���A������P�̑��x��0�C������Q�̑��x��
�̌�A�Ђ�������A�T�D�̍l�@���A������P�̑��x��0�C������Q�̑��x��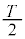 �ƂȂ�܂��B
�ƂȂ�܂��B ������Q�́A�������ɉ^�����J�n���A����0���玞��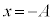 �܂ł̒P�U���Ɠ��l�̒P�U�������āA��U�A�˂̍ő�L�т̈ʒu
�܂ł̒P�U���Ɠ��l�̒P�U�������āA��U�A�˂̍ő�L�т̈ʒu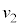 �܂ŗ���(�Ђ��������Ă���
�܂ŗ���(�Ђ��������Ă���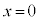 �Ȃ̂ŏ�����Q�͏�����P�Ƃ͏Փ˂��܂���)���]���A���x
�Ȃ̂ŏ�����Q�͏�����P�Ƃ͏Փ˂��܂���)���]���A���x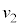 ��
��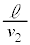 �ɖ߂����Ƃ���łЂ�������A������P�̑��x��
�ɖ߂����Ƃ���łЂ�������A������P�̑��x��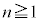 �C������Q�̑��x��0�ɂȂ�܂��B����Ɏ���
�C������Q�̑��x��0�ɂȂ�܂��B����Ɏ���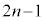 �̌�A3��ڂ̏Փ˂��N���A�Ȍ�A�����^�����J��Ԃ��܂��B
�̌�A3��ڂ̏Փ˂��N���A�Ȍ�A�����^�����J��Ԃ��܂��B
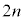 �Ƃ��āA
�Ƃ��āA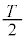 ��ڂ̏Փ˂���
��ڂ̏Փ˂���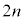 ��ڂ̏Փ˂܂ł̎��Ԃ́A��6�Ō����悤�ɒP�U���̔�����
��ڂ̏Փ˂܂ł̎��Ԃ́A��6�Ō����悤�ɒP�U���̔�����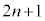 �ł��B
�ł��B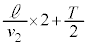 ��ڂ���
��ڂ���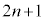 ��ڂ̏Փ˂܂ł̎��Ԃ́A��L�ōl�@����2��ڂ���3��ڂ̏Փ˂܂ł̎��ԂƓ������A
��ڂ̏Փ˂܂ł̎��Ԃ́A��L�ōl�@����2��ڂ���3��ڂ̏Փ˂܂ł̎��ԂƓ������A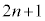 �ł��B�����A
�ł��B�����A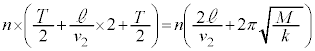 ��ڂ̏Փ˂���
��ڂ̏Փ˂���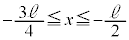 ��ڂ̏Փ˂܂ł̎��Ԃ́A
��ڂ̏Փ˂܂ł̎��Ԃ́A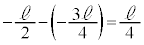 �ł��B
�ł��B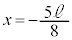 (1��ڂ̏Փ˂̎���)����
(1��ڂ̏Փ˂̎���)����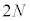 ��ڂ܂ł̏Փ˂ŁA���ꂪn��J��Ԃ���܂��B
��ڂ܂ł̏Փ˂ŁA���ꂪn��J��Ԃ���܂��B
����āA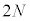 �悿�A
�悿�A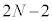 ��ڂ̏Փ˂̎����́A
��ڂ̏Փ˂̎����́A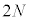 ......[��]
......[��]
�V�D��8�@��蕶�ɁA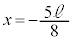 ��2��ڂ̏Փ˂��N�����Ə�����Ă���̂ŁA�U��
��2��ڂ̏Փ˂��N�����Ə�����Ă���̂ŁA�U��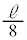 �Ƃ��������͖�������Ă���Ƃ��čl���܂��B
�Ƃ��������͖�������Ă���Ƃ��čl���܂��B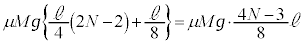 �̗̈�A(���́A
�̗̈�A(���́A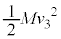 )���ň�U�~�܂�ƁA���C�������C����Î~���C�ɕς��Î~�����܂܂ɂȂ�܂�(���C�����Q��)�B�]���āA
)���ň�U�~�܂�ƁA���C�������C����Î~���C�ɕς��Î~�����܂܂ɂȂ�܂�(���C�����Q��)�B�]���āA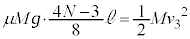 �ŐÎ~����Ƃ��ȊO�́A������P�́A�̈�A��Î~���邱�ƂȂ��ʉ߂��Ă������ƂɂȂ�܂��B��7�Ɠ��l�ɁA
�ŐÎ~����Ƃ��ȊO�́A������P�́A�̈�A��Î~���邱�ƂȂ��ʉ߂��Ă������ƂɂȂ�܂��B��7�Ɠ��l�ɁA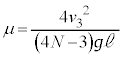 ��ڂ̏Փˌ�A������P�́A�܂��������ɗ̈�A�ɓ���A�̈�A��ʉ߂���A�Ђ��������ď�����Q���P�U��������ɂЂ��������āA������P�́A�E�����ɗ̈�A�ɓ���܂��B�̈�A��ʉ߂���A
��ڂ̏Փˌ�A������P�́A�܂��������ɗ̈�A�ɓ���A�̈�A��ʉ߂���A�Ђ��������ď�����Q���P�U��������ɂЂ��������āA������P�́A�E�����ɗ̈�A�ɓ���܂��B�̈�A��ʉ߂���A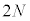 ��ڂ̏Փ˂����܂��B
��ڂ̏Փ˂����܂��B �ŏ��̏Փ�(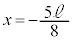 )��A2��ڂ̏Փ˂܂łɁA������P�́A�̈�A��ʉ߂��܂���B4��ڂ̏Փ˂܂łɁA������P�́A�̈�A��2��ʉ߂��܂��B6��ڂ̏Փ˂܂łɁA������P�́A�̈�A��4��ʉ߂��܂��B
)��A2��ڂ̏Փ˂܂łɁA������P�́A�̈�A��ʉ߂��܂���B4��ڂ̏Փ˂܂łɁA������P�́A�̈�A��2��ʉ߂��܂��B6��ڂ̏Փ˂܂łɁA������P�́A�̈�A��4��ʉ߂��܂��B
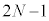 ��ڂ̏Փ˂܂łɁA������P�́A�̈�A��
��ڂ̏Փ˂܂łɁA������P�́A�̈�A��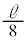 ��ʉ߂��܂��B
��ʉ߂��܂��B
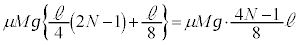 ��ڂ̏Փˌ�A�������ɗ̈�A��ʉ߂��Ă���Ԃ�
��ڂ̏Փˌ�A�������ɗ̈�A��ʉ߂��Ă���Ԃ�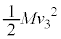 �ŐÎ~����Ƃ�(�̈�A������������
�ŐÎ~����Ƃ�(�̈�A������������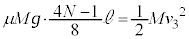 )�A�����C�͂��d���ɂ���Ď�����G�l���M�[��(�G�l���M�[�̌������Q��)�A�̈�A�̒�����
)�A�����C�͂��d���ɂ���Ď�����G�l���M�[��(�G�l���M�[�̌������Q��)�A�̈�A�̒�����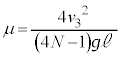 �Ȃ̂ŁA
�Ȃ̂ŁA 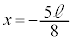 �@����E
�@����E�Î~�����Ƃ��̉^���G�l���M�[��0�ŁA�E�́A�ŏ��ɏ�����P�������Ă����^���G�l���M�[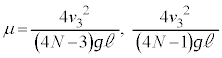 �ɓ������̂ŁA
�ɓ������̂ŁA �� 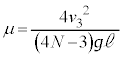
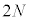 ��ڂ̏Փˌ�A������P���A�������ɗ̈�A��ʉ߂�����A�E�����ɗ̈�A��ʉ߂��Ă���Ԃ�
��ڂ̏Փˌ�A������P���A�������ɗ̈�A��ʉ߂�����A�E�����ɗ̈�A��ʉ߂��Ă���Ԃ�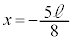 �ŐÎ~����Ƃ��A���ɗ̈�A��
�ŐÎ~����Ƃ��A���ɗ̈�A��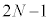 ��ʉ߂��A����ɗ̈�A����
��ʉ߂��A����ɗ̈�A����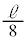 ���������܂��B�����C�͂̎d���ɂ���Ď�����G�l���M�[�́A�E�Ɠ��l�ɁA
���������܂��B�����C�͂̎d���ɂ���Ď�����G�l���M�[�́A�E�Ɠ��l�ɁA ���ꂪ�A�ŏ��ɏ�����P�������Ă����^���G�l���M�[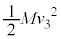 �ɓ������̂ŁA
�ɓ������̂ŁA �� 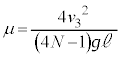
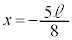 �ŐÎ~����̂͏�L2�ʂ�̏ꍇ�����ł��B����āA�����C�W��μ����肤��l�́A
�ŐÎ~����̂͏�L2�ʂ�̏ꍇ�����ł��B����āA�����C�W��μ����肤��l�́A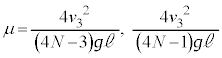 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 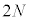 ......[��]
......[��]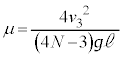
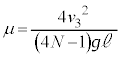
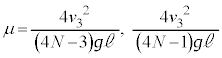 ......[��]
......[��]