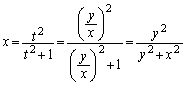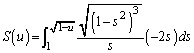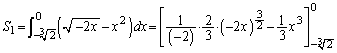山梨大医数学'09年[4]
放物線A: 上の点
上の点 (
( )における接線に関して、Aの頂点と対称な点Pのx座標、y座標を
)における接線に関して、Aの頂点と対称な点Pのx座標、y座標を ,
,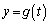 と表し、
と表し、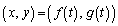 が描く曲線をBとする。
が描く曲線をBとする。
(2)  とする。
とする。 を満たす実数uに対して、曲線Bとx軸、直線
を満たす実数uに対して、曲線Bとx軸、直線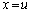 によって囲まれる図形の面積を
によって囲まれる図形の面積を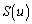 とするとき、
とするとき、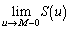 を求めよ。
を求めよ。 (3) 直線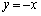 に関して放物線Aと対称な放物線をCとする。放物線Cをy軸方向に2倍拡大した放物線をDとする。放物線Dと放物線Aによって囲まれる図形の面積を求めよ。
に関して放物線Aと対称な放物線をCとする。放物線Cをy軸方向に2倍拡大した放物線をDとする。放物線Dと放物線Aによって囲まれる図形の面積を求めよ。 (4) 直線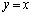 と放物線Dによって囲まれる図形を直線
と放物線Dによって囲まれる図形を直線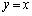 の周りに1回転してできる立体の体積を求めよ。
の周りに1回転してできる立体の体積を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
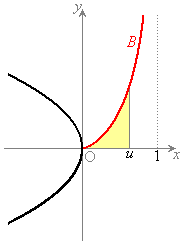
解答 数学Ⅲ全般にわたってボリューム満点のこういう問題こそ、入試準備の演習課題として効率的で最適、という問題です。(3)の定積分は素直に計算すると、xにマイナスがついているのがいやらしく、充分注意して(危なければ、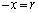 などとおいて置換積分する)計算する必要があります。
などとおいて置換積分する)計算する必要があります。
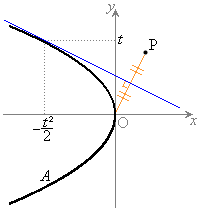 (1) A:
(1) A: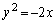
Aの方程式両辺をxで微分して、
点 における接線:
における接線: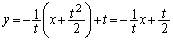 ・・・①
・・・①
原点O(放物線Aの頂点)を通り①と垂直な直線: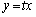 ・・・②
・・・②
①,②を連立して、 ∴  ②より、
②より、 Aの頂点と点P(①に関してAの頂点と対称)を結ぶ線分OPの中点が、①と②の交点になります。よって、Pの座標は
Aの頂点と点P(①に関してAの頂点と対称)を結ぶ線分OPの中点が、①と②の交点になります。よって、Pの座標は
∴  ,
,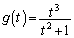 ......[答]
......[答]
 (2)
(2) 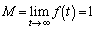 です。
です。 ,
, より、
より、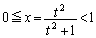 であることに注意します。
であることに注意します。
 のときP
のときP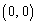 ですが、
ですが、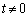 のとき、
のとき、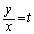 より、
より、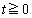 より
より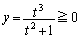 なので、
なので、これが曲線Bの方程式になります。 のとき
のとき なので
なので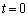 の場合を含んでいます。曲線Bとx軸、直線
の場合を含んでいます。曲線Bとx軸、直線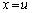 (
( )によって囲まれる図形(右図黄色着色部分)の面積
)によって囲まれる図形(右図黄色着色部分)の面積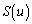 は、
は、 (分母がなるべく簡単な形になるように)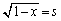 とおくと、
とおくと、 ,
,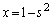
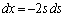 ,x:
,x: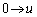 のとき、s:
のとき、s: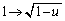 (置換積分を参照)
(置換積分を参照)
放物線Cをy軸方向に2倍拡大した放物線D: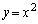 A,Dの交点は、
A,Dの交点は、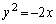 と
と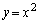 を連立して、
を連立して、 放物線Dと放物線Aによって囲まれる図形(右図黄緑色着色部分)の面積 は、
は、 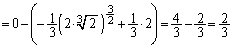 ......[答]
......[答]
∴ 
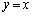 の周りに回転させる回転体ですが、x軸の周りに回転させるときと同様に考えて、回転軸に垂直な断面の円の面積を、回転軸に沿って積分することにより回転体の体積を求めます(斜回転体を参照)。
の周りに回転させる回転体ですが、x軸の周りに回転させるときと同様に考えて、回転軸に垂直な断面の円の面積を、回転軸に沿って積分することにより回転体の体積を求めます(斜回転体を参照)。
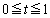 として、D上の点Q
として、D上の点Q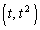 を通り
を通り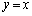 に垂直な直線は、
に垂直な直線は、 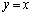 と連立して、交点Hのx座標を求めると、
と連立して、交点Hのx座標を求めると、 において
において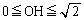 より、回転体の体積Vは、
より、回転体の体積Vは、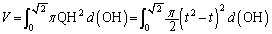 (回転軸に沿って積分するので、tではなく、OHについて積分する)
(回転軸に沿って積分するので、tではなく、OHについて積分する)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。