��啨��'24�N�O��[3]
�ȉ���A��B�̗����̖��ɉ���B�Ȃ�A��B�͓Ɨ��������e�̖��ł���B
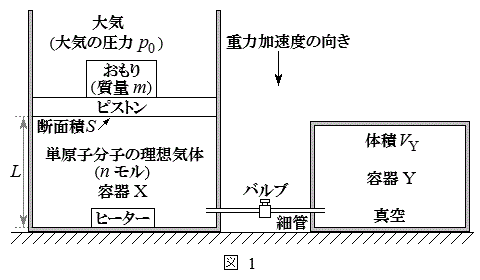 A�D�}1�Ɏ����悤�ɁA��C�����ʼn~���e��X��Y�������ȏ��ɌŒ肳��Ă���B�e��X��Y�͍ǂƃo���u(�R�b�N)����ē������Ȃ����Ă���B�e��X���̃s�X�g���́A�f�ʐ�S�̒�ʂ������A���������ɖ��C�Ȃ��Ŋ��炩�ɓ������Ƃ��ł���B�܂��A�s�X�g���̈ʒu�͌Œ肷�邱�Ƃ��ł���B�e��X�̒��ɂ̓q�[�^�[������A�C�̂̉��x���グ�邱�Ƃ��ł���B�e��Y���̑̐ς�
A�D�}1�Ɏ����悤�ɁA��C�����ʼn~���e��X��Y�������ȏ��ɌŒ肳��Ă���B�e��X��Y�͍ǂƃo���u(�R�b�N)����ē������Ȃ����Ă���B�e��X���̃s�X�g���́A�f�ʐ�S�̒�ʂ������A���������ɖ��C�Ȃ��Ŋ��炩�ɓ������Ƃ��ł���B�܂��A�s�X�g���̈ʒu�͌Œ肷�邱�Ƃ��ł���B�e��X�̒��ɂ̓q�[�^�[������A�C�̂̉��x���グ�邱�Ƃ��ł���B�e��Y���̑̐ς�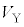 �ł���B
�ł���B
�ŏ��A�ǂ̃o���u�͕����Ă���B�e��X���ɂ�n�����̒P���q���q�̗��z�C�̂������Ă���A�e��Y���͐^��ƂȂ��Ă���B�܂��A�s�X�g���Ɏ���m�̂����肪�̂����Ă���B
���ׂĂ̗e��A�ǁA�o���u��s�X�g���͒f�M�ޗ��ō���Ă���B�܂��A�s�X�g���̎��ʁA�ǂ̑̐ρA�q�[�^�[�̑̐ς���уq�[�^�[�̔M�e�ʂ͖����ł�����̂Ƃ���B�C�̒萔��R�C�d�͉����x�̑傫����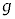 �C��C�̈��͂�
�C��C�̈��͂�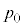 �Ƃ��Ĉȉ��̖�ɓ�����B�Ȃ��A�P���q���q�̗��z�C�̂̂������Ƃ����f�M�ω��ł́A����p�Ƒ̐�V���u
�Ƃ��Ĉȉ��̖�ɓ�����B�Ȃ��A�P���q���q�̗��z�C�̂̂������Ƃ����f�M�ω��ł́A����p�Ƒ̐�V���u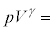 ���v�̊W�����Bγ�͔�M��Ƃ���萔�ł���B�܂��A��C�̈���
���v�̊W�����Bγ�͔�M��Ƃ���萔�ł���B�܂��A��C�̈���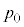 �͈��ŁA�e����̋C�̂̕��q�ɂ͂��炭�d�͖͂����ł�����̂Ƃ���B
�͈��ŁA�e����̋C�̂̕��q�ɂ͂��炭�d�͖͂����ł�����̂Ƃ���B
��1�@�͂��߂Ƀs�X�g�������R�ɓ������Ԃɂ����B����ƁA�s�X�g���́A�}1�̂悤�ɂ��̒�ʂ��e��X���̒�ʂ��獂��L�̈ʒu�ŐÎ~���Ă����B���̂Ƃ��̗e��X���̋C�̂̉��x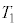 ���A
���A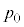 �Cm�C
�Cm�C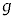 �CS�CL�Cn�CR�̂����K�v�Ȃ��̂�p���ĕ\���B
�CS�CL�Cn�CR�̂����K�v�Ȃ��̂�p���ĕ\���B ��2�@��1�̏��(���x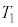 )����A�s�X�g���̒�ʂ�����L�̈ʒu�̂܂܌Œ肵�A�o���u���J�����B����ƁA�C�̂͗e��Y���ɍL���邾���ŗe��̕ǂ�s�X�g���ɑ��Ďd���������A�o���u���J���ď\���Ɏ��Ԃ��o�߂�����ɁA�e��X����Y���̋C�̂̉��x�ƈ��͓͂������Ȃ����B���̂Ƃ��̋C�̂̉��x
)����A�s�X�g���̒�ʂ�����L�̈ʒu�̂܂܌Œ肵�A�o���u���J�����B����ƁA�C�̂͗e��Y���ɍL���邾���ŗe��̕ǂ�s�X�g���ɑ��Ďd���������A�o���u���J���ď\���Ɏ��Ԃ��o�߂�����ɁA�e��X����Y���̋C�̂̉��x�ƈ��͓͂������Ȃ����B���̂Ƃ��̋C�̂̉��x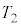 ���A
���A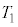 �C
�C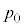 �Cm�C
�Cm�C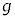 �CS�CL�C
�CS�CL�C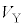 �̂����K�v�Ȃ��̂�p���ĕ\���B
�̂����K�v�Ȃ��̂�p���ĕ\���B ��3�@��2�̏�Ԃ���A�o���u���J�����܂܃q�[�^�[��p���ėe��X����Y���̋C�̂̉��x��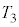 �܂ŏ㏸�����āA�s�X�g���̌Œ���O�����B����ƁA�s�X�g���̒�ʂ͍���L�̈ʒu�ŕς��Ȃ������B���̂Ƃ��̋C�̂̉��x
�܂ŏ㏸�����āA�s�X�g���̌Œ���O�����B����ƁA�s�X�g���̒�ʂ͍���L�̈ʒu�ŕς��Ȃ������B���̂Ƃ��̋C�̂̉��x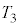 ���A
���A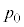 �Cm�C
�Cm�C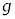 �CS�CL�C
�CS�CL�C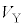 �Cn�CR�̂����K�v�Ȃ��̂�p���ĕ\���B
�Cn�CR�̂����K�v�Ȃ��̂�p���ĕ\���B ��4�@��3�̏�Ԃ���A�o���u���Ăѕ��āA��������s�X�g������������ƊO�����B����ƁA�e��X���̋C�̂ɂ����āA�������Ƃ����f�M�ω����N����A�s�X�g���̒�ʂ͍���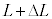 �̈ʒu�ƂȂ����B���̂Ƃ��A
�̈ʒu�ƂȂ����B���̂Ƃ��A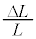 ���A
���A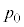 �Cm�C
�Cm�C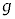 �CS�Cγ�Cn�CR�̂����K�v�Ȃ��̂�p���ĕ\���B
�CS�Cγ�Cn�CR�̂����K�v�Ȃ��̂�p���ĕ\���B ��5�@�ȉ��̕��͂� ��
�� �ɓ���ׂ������A���ꂼ���
�ɓ���ׂ������A���ꂼ��� �̒��ɗ^����ꂽ�����̂����K�v�Ȃ��̂�p���ĕ\���B
�̒��ɗ^����ꂽ�����̂����K�v�Ȃ��̂�p���ĕ\���B
��3����і�4�̉ߒ��ɂ���������G�l���M�[�ω��Ǝd�������߂Ă݂悤�B�܂��A��3�̑���ɂ����āA�q�[�^�[�ɂ���ėe��X����Y���̋C�̂�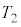 ����
����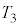 �܂ʼn��߂����Ƃɂ������G�l���M�[�̕ω�
�܂ʼn��߂����Ƃɂ������G�l���M�[�̕ω�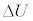 ��
�� �ƂȂ�B�܂��A��4�̒f�M�ω��ŋC�̂��s�X�g���ɑ��čs�����d��W��
�ƕ\����B
��6�@��3�̏�Ԃ���A�o���u���J�����܂܁A��������s�X�g������������ƊO�����B����ƁA�e��X����Y���̋C�̂ɂ����āA�������Ƃ����f�M�ω����N����A�s�X�g���̒�ʂ͍���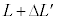 �̈ʒu�ƂȂ����B���̂Ƃ��A
�̈ʒu�ƂȂ����B���̂Ƃ��A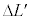 �Ɩ�4�ŋ��߂�
�Ɩ�4�ŋ��߂�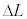 �̔�
�̔�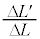 ���AL�CS�C
���AL�CS�C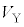 �̂����K�v�Ȃ��̂�p���ĕ\���B
�̂����K�v�Ȃ��̂�p���ĕ\���B
B�D�����q�ߑ��Ö@�Ƃ́A����זE�Ɏ�荞�܂ꂽ���q�jX�ƒ����q�Ƃ̊j�����Ő��������α��(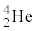 �̌��q�j)�ɂ���āA����זE�������I�Ɏ��ł�������ː��Ö@�̈�ł���B
�̌��q�j)�ɂ���āA����זE�������I�Ɏ��ł�������ː��Ö@�̈�ł���B
�T�D�Î~���Ă��錴�q�jX�ɒx�������q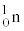 �Ă��Ƃ���A�j����
�Ă��Ƃ���A�j���� ���N����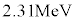 (
(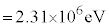 )�̃G�l���M�[���������B�����āA���̂��ׂẴG�l���M�[��
)�̃G�l���M�[���������B�����āA���̂��ׂẴG�l���M�[��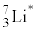 ��
��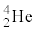 �̌��q�j�̉^���G�l���M�[�ɕϊ����ꂽ�B������
�̌��q�j�̉^���G�l���M�[�ɕϊ����ꂽ�B������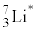 ��
��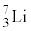 �̗�N��Ԃł���B�Ȃ��A
�̗�N��Ԃł���B�Ȃ��A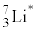 �́A
�́A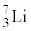 �Ɠ������̗z�q�ƒ����q����\������Ă��邪�A�\1�Ɏ����悤��
�Ɠ������̗z�q�ƒ����q����\������Ă��邪�A�\1�Ɏ����悤��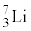 �ɔ�ׂđ傫�Ȏ��ʂ����B
�ɔ�ׂđ傫�Ȏ��ʂ����B
��7�@���q�jX�̎��ʐ��ƌ��q�ԍ������߂�B
��8�@��L�̊j�������N����A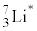 ��
��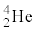 �̂��݂��ɏ\���ɗ��ꂽ���
�̂��݂��ɏ\���ɗ��ꂽ���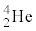 �̉^���G�l���M�[���AMeV��P�ʂƂ��ėL������2���ŋ��߂�B�������A�j�����̑O��ł͉^���ʕۑ��������藧�B�܂��A�j�����O�̒����q�̉^���ʂ͖����ł�����̂Ƃ���B�K�v�ł���A�\1�̌��q�j�̎��ʂ̕����l��p���Ă��悢�B
�̉^���G�l���M�[���AMeV��P�ʂƂ��ėL������2���ŋ��߂�B�������A�j�����̑O��ł͉^���ʕۑ��������藧�B�܂��A�j�����O�̒����q�̉^���ʂ͖����ł�����̂Ƃ���B�K�v�ł���A�\1�̌��q�j�̎��ʂ̕����l��p���Ă��悢�B
�\1
�U�D�ŋ߂̒����q�ߑ��Ö@�ł́A�T�C�N���g�����Ȃǂ̉������p����B�����ł́A���\MeV�̉^���G�l���M�[�܂ʼn������ꂽ�z�q���A���`�E����x�����E���Ɗj���������邱�ƂŁA��MeV���x�̉^���G�l���M�[���������q��������B���̌�A�������������q�������ނɓ��˂��A���ÂɓK�����^���G�l���M�[�܂Ō���������B
��9�@����(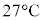 )�ŔM�^�����Ă��钆���q�̏W�܂��P���q���q�̗��z�C�̂Ƃ݂Ȃ����Ƃ��A�����q1������̕��ς̉^���G�l���M�[���AeV��P�ʂƂ��ėL������2���ŋ��߂�B�K�v�ł���A�{���c�}���萔
)�ŔM�^�����Ă��钆���q�̏W�܂��P���q���q�̗��z�C�̂Ƃ݂Ȃ����Ƃ��A�����q1������̕��ς̉^���G�l���M�[���AeV��P�ʂƂ��ėL������2���ŋ��߂�B�K�v�ł���A�{���c�}���萔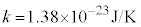 �Ɠd�C�f��
�Ɠd�C�f��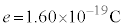 ��p���Ă悢�B
��p���Ă悢�B
���������ނƂ��ėp���Ē����q������������ꍇ�A��ɐ��Ɋ܂܂�鐅�f���q���̗z�q�Ƃ̏Փ˂ɂ�蒆���q�͉^���G�l���M�[�������B���̏Փ˂��A�����q�ƐÎ~�����z�q�Ƃ̒e���Փ˂Ƃ��čl���悤�B
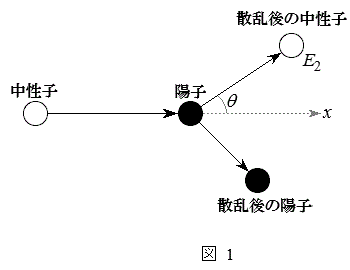 ��10�@�}1�̂悤�ɁAx���̐��̌����ɉ^�����钆���q���A�Î~���Ă���z�q�ɏՓ˂����B���̌�A�����q��x���̐��̌�������p�xθ(
��10�@�}1�̂悤�ɁAx���̐��̌����ɉ^�����钆���q���A�Î~���Ă���z�q�ɏՓ˂����B���̌�A�����q��x���̐��̌�������p�xθ(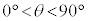 )�̕����֎U�����ꂽ�B���̎U���Œ����q�̉^���G�l���M�[��
)�̕����֎U�����ꂽ�B���̎U���Œ����q�̉^���G�l���M�[��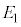 ����
����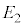 �Ɍ��������B���̂Ƃ��̉^���G�l���M�[�̔�
�Ɍ��������B���̂Ƃ��̉^���G�l���M�[�̔�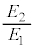 ��θ��p���ĕ\���B�������A�z�q�ƒ����q�͓������ʂ����Ƃ݂Ȃ��Ă悢�B
��θ��p���ĕ\���B�������A�z�q�ƒ����q�͓������ʂ����Ƃ݂Ȃ��Ă悢�B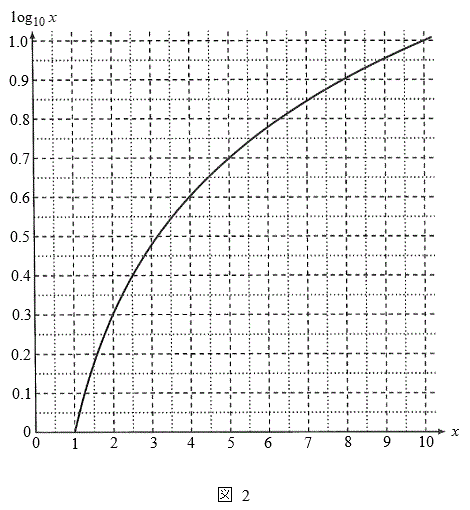 ��11�@��10�ɂ����āA�����q�̎U�����\�ȕ����ɓ��m���ŋN����ꍇ�A�����q�̉^���G�l���M�[��1��̏Փ˂ŕ���
��11�@��10�ɂ����āA�����q�̎U�����\�ȕ����ɓ��m���ŋN����ꍇ�A�����q�̉^���G�l���M�[��1��̏Փ˂ŕ���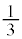 �{�ɂȂ�B�ȉ��ł͒����q�͐����ŗz�q�Ƃ̂ݏՓ˂��A1��̏Փ˂ɂ��^���G�l���M�[��
�{�ɂȂ�B�ȉ��ł͒����q�͐����ŗz�q�Ƃ̂ݏՓ˂��A1��̏Փ˂ɂ��^���G�l���M�[��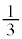 �{�Ɍ�������ƒP�������čl����B
�{�Ɍ�������ƒP�������čl����B
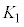 �̉^���G�l���M�[���������q���z�q��N��Փ˂������ʁA
�̉^���G�l���M�[���������q���z�q��N��Փ˂������ʁA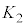 �̉^���G�l���M�[�܂Ō��������B���̂Ƃ��AN��
�̉^���G�l���M�[�܂Ō��������B���̂Ƃ��AN��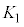 ��
��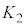 ��p���ĕ\���B
��p���ĕ\���B
�܂��A10MeV�̉^���G�l���M�[���������q���A��9�ŋ��߂����ς̉^���G�l���M�[�ȉ��܂Ō�������ɂ́A�Œች��̏Փ˂��N�����K�v�����邩���߂�B�������A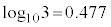 �Ƃ���B�K�v�ł���A�}2�̏�p�ΐ��̃O���t��p���Ă悢�B
�Ƃ���B�K�v�ł���A�}2�̏�p�ΐ��̃O���t��p���Ă悢�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�O���͒f�M�ω��̖��A�㔼�͕��ː���Â��l�^�ɂ������q�j�̖��ł��B���q�j����͏o��p�x�͏������ł����A���̕��A�{��̂悤�ɈՂ������Ƃ������̂ŁA���Ō��q�j������X���[���Ă͂����܂���B
A�D��1�@�e��X���̋C�̂̈��͂�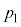 �Ƃ��āA�s�X�g���ɓ����͂̂荇�����A
�Ƃ��āA�s�X�g���ɓ����͂̂荇�����A 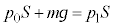 �@��
�@�� 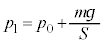 �@����@
�@����@�@���A
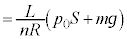 ......[��]
......[��]
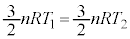 �@��
�@�� 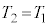 ......[��]
......[��]
��3�@�s�X�g���ɓ����͂̏ɕω��͂Ȃ��A���x�㏸��̋C�̂̈��͂�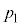 �ł��B�s�X�g���̌Œ���O������̏�ԕ������́A
�ł��B�s�X�g���̌Œ���O������̏�ԕ������́A �@���A
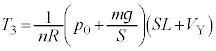 ......[��]
......[��]
��4�@��3�̏�Ԃ���o���u�����ƁA���͂�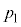 �̂܂܂ő̐ς�
�̂܂܂ő̐ς�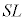 �ƂȂ�܂��B��������O�����f�M�ω���ɁA�̐ς�
�ƂȂ�܂��B��������O�����f�M�ω���ɁA�̐ς�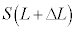 �ƂȂ�A�e����̋C�̂̈��͂͑�C��
�ƂȂ�A�e����̋C�̂̈��͂͑�C��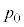 �ɓ������Ȃ�܂��B�|�A�b�\���̊W�����A
�ɓ������Ȃ�܂��B�|�A�b�\���̊W�����A �@���A
��5�@��3�̉ߒ��ɂ����āA�C�̂̉��x�́A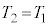 ����
����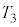 �܂ŕω�����̂ŁA�����G�l���M�[�̕ω�
�܂ŕω�����̂ŁA�����G�l���M�[�̕ω�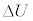 �́A��1�C��3�̌��ʂ�p���āA
�́A��1�C��3�̌��ʂ�p���āA ��3�ŏ������悤�ɁA�f�M�ω�������O(�o���u�������)�̗e��X���̋C�̂̈��͂�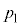 �C�̐ς�
�C�̐ς�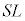 �C���x��
�C���x��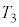 �ł��B��ԕ������́A
�ł��B��ԕ������́A 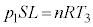 �@����B
�@����B��4�ŏ������悤�ɁA��������O���Ēf�M�ω�������̗e��X���̋C�̂̈��͂�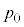 �C�̐ς�
�C�̐ς�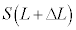 �ł��B���̂Ƃ��̋C�̂̉��x��
�ł��B���̂Ƃ��̋C�̂̉��x��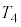 �Ƃ��āA
�Ƃ��āA
�̋C�̂̏�ԕ������́A 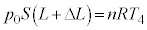 �@����C
�@����C��4�̉ߒ��ł́A�f�M�ω��Ȃ̂��M�͊w��1�@�����A�C�̂̂����d��W�͓����G�l���M�[�̌������ɓ������Ȃ�̂ŁA�B�C�C���A
��6�@��3�ŏ������悤�ɁA�o���u���J�����܂܂�������O��������̋C�̂̈��͂�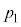 �C�̐ς�
�C�̐ς�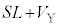 �ł��B
�ł��B ��4�ŏ������悤�ɁA�f�M�ω���̈��͂�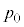 �C�̐ς�
�C�̐ς�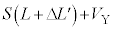 �ł��B�|�A�b�\���̊W�����A
�ł��B�|�A�b�\���̊W�����A �D�ƇA�ʼnE�ӂ��������̂ŁA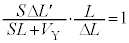
�� 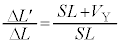 ......[��]
......[��]
B�D�T�D��7�@���q�jX�̎��ʐ���A�C���q�ԍ���Z�Ƃ����(���q�j���Q��)�A�j�����O��ŁA���ʐ��A���q�ԍ��̘a�͕ω����Ȃ��̂ŁA 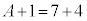 �C
�C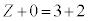
�� ���ʐ��F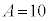 ......[��]�C���q�ԍ��F
......[��]�C���q�ԍ��F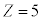 ......[��]
......[��]
��8�@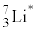 �C
�C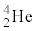 �̎��ʂ�M�Cm�C
�̎��ʂ�M�Cm�C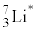 �C
�C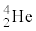 �̊j������̑�����V�Cv�Ƃ���ƁA�^���ʕۑ����A
�̊j������̑�����V�Cv�Ƃ���ƁA�^���ʕۑ����A 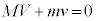 �@��
�@�� 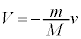 �@����E
�@����E����āA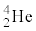 �̉^���G�l���M�[�́A�\1�̃f�[�^��p���āA
�̉^���G�l���M�[�́A�\1�̃f�[�^��p���āA 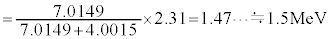 ......[��]
......[��]
�����q1�̕��ς̑�����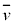 �Ƃ��āA���ς̉^���G�l���M�[��(�C�̕��q�^���_���Q��)�A
�Ƃ��āA���ς̉^���G�l���M�[��(�C�̕��q�^���_���Q��)�A 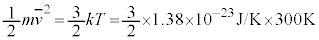 �@(
�@(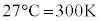 )
)���̃G�l���M�[��eV�P�ʂŕ\���ƁA
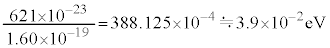 ......[��]
......[��]
��10�@�z�q�A�����q�̎��ʂ�m�C�U���O�̒����q�̑�����v�C�U����̒����q�A�z�q�̑�����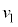 �C
�C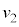 �C�U����̗z�q�̐i�s������x���̂Ȃ��p��φ�Ƃ���ƁA�U���O��̉^���ʕۑ����A
�C�U����̗z�q�̐i�s������x���̂Ȃ��p��φ�Ƃ���ƁA�U���O��̉^���ʕۑ����A 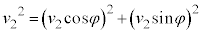 ���A
���A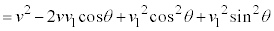
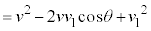 �@����F
�@����F���D�^���ʕۑ��̃x�N�g���}��`���A�]���藝����F�������܂��B �U���O��̃G�l���M�[�ۑ����A
m�Ŋ���2�������A�F�������āA
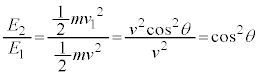 ......[��]
......[��]
�}2���A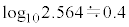 (���m�ɂ�
(���m�ɂ�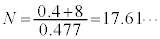 �ł�)�Ȃ̂ŁA
�ł�)�Ȃ̂ŁA ����āA��9�ŋ��߂����ς̉^���G�l���M�[�ȉ��܂Ō�������ɂ́A�Œ�18�� ......[��]�@�̏Փ˂��N�����K�v������܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 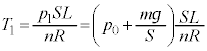
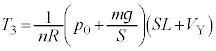 ......[��]
......[��]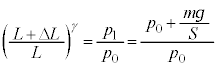
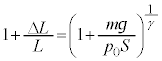 �@��
�@�� 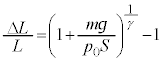 ......[��]�@����A
......[��]�@����A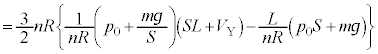
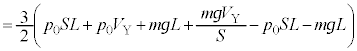
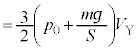 ......[��]
......[��]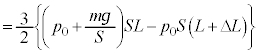 �@(�� �@)
�@(�� �@)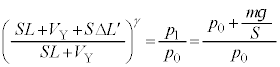
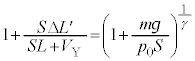 �@��
�@�� 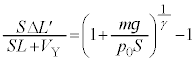 �@����D
�@����D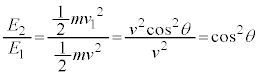 ......[��]
......[��]