���啨��'05�N�O��[1]
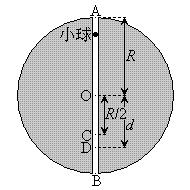 �@�}1�̂悤�ɁA�n���̒��SO��ʂ�A�n�\�̂���n�_A�ƒn�_B�Ƃ����ԍג����g���l�����ɂ����鏬���̒����^�����l����B�n���aR�C��l�Ȗ��xρ�̋��Ƃ݂Ȃ��A���L���͒萔��G�Ƃ��Ĉȉ��̊e��ɓ�����B�Ȃ��A�n���̒��SO���狗��r�̈ʒu�ɂ����ď������n�������͂́A���SO���狗��r�ȓ��ɂ���n���̕����̎��ʂ����SO�ɏW�܂����Ɖ��肵���ꍇ�ɁA�������閜�L���͂ɓ������B�������A�n���̎��]�ƌ��]�̉e���A�g���l���Ə����̊Ԃ̖��C����ы�C��R�͖���������̂Ƃ��A�n���̎��ʂ͏����̎��ʂɔ�\���傫�����̂Ƃ���B
�@�}1�̂悤�ɁA�n���̒��SO��ʂ�A�n�\�̂���n�_A�ƒn�_B�Ƃ����ԍג����g���l�����ɂ����鏬���̒����^�����l����B�n���aR�C��l�Ȗ��xρ�̋��Ƃ݂Ȃ��A���L���͒萔��G�Ƃ��Ĉȉ��̊e��ɓ�����B�Ȃ��A�n���̒��SO���狗��r�̈ʒu�ɂ����ď������n�������͂́A���SO���狗��r�ȓ��ɂ���n���̕����̎��ʂ����SO�ɏW�܂����Ɖ��肵���ꍇ�ɁA�������閜�L���͂ɓ������B�������A�n���̎��]�ƌ��]�̉e���A�g���l���Ə����̊Ԃ̖��C����ы�C��R�͖���������̂Ƃ��A�n���̎��ʂ͏����̎��ʂɔ�\���傫�����̂Ƃ���B
�T�@����m�̏�����n�_A����Â��ɂ͂Ȃ����Ƃ��̉^�����l����B
(1) �������n���̒��SO���狗��r (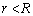 )�̈ʒu�ɂ��鎞�A�����ɓ����͂̑傫�������߂�B
)�̈ʒu�ɂ��鎞�A�����ɓ����͂̑傫�������߂�B (2) �������^���J�n��A�͂��߂Ēn�_A�ɖ߂��Ă���܂ł̎���T�����߂�B
�U�@��������m������̏���P�CQ�̉^�����l����B����0�ɏ���P���A����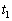 �ɏ���Q��̒n�_A�ŐÂ��ɂ͂Ȃ����Ƃ���A��̏�����OB�̒��_C�ŏՓ˂����B�����œ�̏����Ԃ̂͂˂�����W����0�Ƃ��A�Փˌ��̏����͈�̂ƂȂ��ĉ^��������̂Ƃ���B�������A
�ɏ���Q��̒n�_A�ŐÂ��ɂ͂Ȃ����Ƃ���A��̏�����OB�̒��_C�ŏՓ˂����B�����œ�̏����Ԃ̂͂˂�����W����0�Ƃ��A�Փˌ��̏����͈�̂ƂȂ��ĉ^��������̂Ƃ���B�������A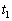 �͖�T(2)�ŋ��߂�����T�������������̂Ƃ���B
�͖�T(2)�ŋ��߂�����T�������������̂Ƃ���B (1) 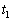 ��T��p���ĕ\���B
��T��p���ĕ\���B (2) ��̏���P�CQ���Փ˂��Ă���͂��߂Ē��SO��ʉ߂���܂ł̎��Ԃ�T��p���ĕ\���B
�V�@��U�Ɠ��l�ɁA����0�ɏ���P���A����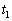 �ɏ���Q��̒n�_A�ŐÂ��ɂ͂Ȃ����B�������A��̏����Ԃ̂͂˂�����W����e (
�ɏ���Q��̒n�_A�ŐÂ��ɂ͂Ȃ����B�������A��̏����Ԃ̂͂˂�����W����e (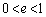 )�Ƃ���B
)�Ƃ���B (1) ��̏������ŏ��ɏՓ˂�����A����P�͒n�_B�Ɍ������ĉ^�����A�n���̒��SO���狗��d�̓_D�ɂ����Ē��SO�Ɍ������Đ܂�Ԃ����B���̂Ƃ���d�̒l���͂˂�����W��e����ђn���̔��aR��p���ĕ\���B
(2) ����P�Ə���Q�����ڂɏՓ˂���ʒu�����߂�B
(3) ���̌��̏����͏Փ˂��J��Ԃ����B�\�����Ԃ��o�߂�����A�ǂ̂悤�ȉ^���ɂȂ邩������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�n���̒��S��ʂ�g���l�����@�����Ƃ��āA���̃g���l�����ŕ��̂��ǂ������^�������邩�Ƃ������ł��B'04�N�Ɉ��Q��w�ł����l�̖�肪�o�肳��Ă��܂��B
�T(1) ���ar�̋����̐���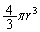 (���̖��ł������̐��̌����͗^�����Ă��Ȃ��̂Ŋo���Ă����K�v������܂�)�C���̕�����������
(���̖��ł������̐��̌����͗^�����Ă��Ȃ��̂Ŋo���Ă����K�v������܂�)�C���̕�����������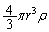
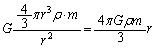 ......[��]
......[��]
(2) O�����_�Ƃ��AOA������x���������Ƃ������W���l���܂��B
���������W��x (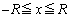 )���Ƃ��āA�����ɂ͂˂ɒ��SO�Ɍ��������������̂ŁA
)���Ƃ��āA�����ɂ͂˂ɒ��SO�Ɍ��������������̂ŁA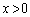 �̂Ƃ���x���������ɁA
�̂Ƃ���x���������ɁA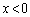 �̂Ƃ���x���������ɁA���������܂��B(1)�̌��ʂ�
�̂Ƃ���x���������ɁA���������܂��B(1)�̌��ʂ�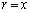 �Ƃ��A�����ɓ������͕����������
�Ƃ��A�����ɓ������͕����������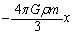 �ƕ\���܂��B
�ƕ\���܂��B
�������^���������́A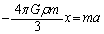 ����@
����@
����́A�o�l�萔��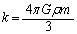 �Ƃ���A�o�l�U��q�̉^���������Ɠ��^�ł��B
�Ƃ���A�o�l�U��q�̉^���������Ɠ��^�ł��B
�]���āA�����́A�p�U����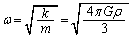 ���P�U�����s���܂��BA�_�𗣂��A�_�ɖ߂�܂ł�����T�́A�P�U���̈�����ɑ������܂��B����āA
���P�U�����s���܂��BA�_�𗣂��A�_�ɖ߂�܂ł�����T�́A�P�U���̈�����ɑ������܂��B����āA 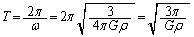 ......[��]
......[��]
�U(1) ����P������0��A�_(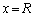 )�ɂ����̂ŁA����t�ɂ�����P�����W��
)�ɂ����̂ŁA����t�ɂ�����P�����W��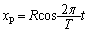 �ƕ\���܂��B
�ƕ\���܂��B ����Q������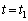 ��A�_�ɂ����̂ŁA����t�ɂ�����Q�����W��
��A�_�ɂ����̂ŁA����t�ɂ�����Q�����W��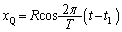 �ƕ\���܂�(Q���^���J�n���Ă����������
�ƕ\���܂�(Q���^���J�n���Ă����������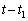 �ł�)�B
�ł�)�B C�_(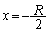 )�ŗ��҂��Փ˂���Ƃ��A���҂����W�͓������A
)�ŗ��҂��Փ˂���Ƃ��A���҂����W�͓������A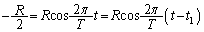
�� 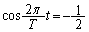 �@��
�@�� 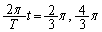 �@��
�@�� 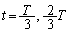 ����A
����A
�܂��A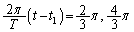 �@��
�@�� 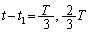 ����B
����B
�A�C�B�C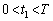 ���A
���A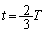 �C
�C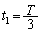 .......[��]�O�p���������o���̂������ł��B���Z�͈̔͂ł��P�U���������~�^�����Ă������̂̐��ˉe�̉^���ƂƂ炦�܂��B���_�𒆐S�Ƃ������aR�̉~�̎����P��Q�������~�^������ƍl����ƁA�_
.......[��]�O�p���������o���̂������ł��B���Z�͈̔͂ł��P�U���������~�^�����Ă������̂̐��ˉe�̉^���ƂƂ炦�܂��B���_�𒆐S�Ƃ������aR�̉~�̎����P��Q�������~�^������ƍl����ƁA�_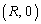 ���o�����āAP���_
���o�����āAP���_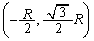 �C�܂���
�C�܂���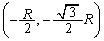 �ɒB����܂łɉ~��
�ɒB����܂łɉ~��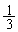 ���C�܂���
���C�܂���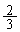 �����܂��BQ���x���
�����܂��BQ���x���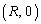 ���o�����āA�t���ɉ����P�Əo��Ƃ���ƁAQ�̕����i�ݕ����������̂ŁA�o��܂łɁAP��
���o�����āA�t���ɉ����P�Əo��Ƃ���ƁAQ�̕����i�ݕ����������̂ŁA�o��܂łɁAP��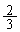 ���CQ��
���CQ��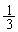 ���܂��悢���ƂɂȂ�܂��B����ŁAP���o�����Ă���Q���o������܂ł�������
���܂��悢���ƂɂȂ�܂��B����ŁAP���o�����Ă���Q���o������܂ł�������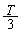 �ƂȂ�܂��B�~��`���čl����قڒ����I�ɖ��炩�ł��B
�ƂȂ�܂��B�~��`���čl����قڒ����I�ɖ��炩�ł��B
(2) P��Q�����x�́A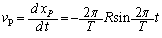 �C
�C
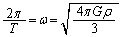 ���A�Փ����̗��҂����x�́A
���A�Փ����̗��҂����x�́A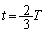 �C
�C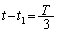 �Ƃ��āA
�Ƃ��āA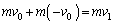 �@��
�@�� 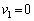
���̌�̑��x��0�Ƃ������Ƃ́A�Փ˒n�_C�_�͍��̌���P�U���̐U���[���Ƃ������Ƃł��B���̌�U���[����U�����SO�܂łɗv���鎞�Ԃ�������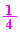 �ł��B
�ł��B
���̌�̉^���������́A�@�ɂ�����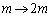 �Ƃ������̂ŁA�p�U�����A�����͍��̑O�ƕς��܂���B����āA���߂������́A
�Ƃ������̂ŁA�p�U�����A�����͍��̑O�ƕς��܂���B����āA���߂������́A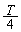 ......[��]���ǂ��̖��������̂ɂ́A�ՓˑO�̑��x������t�������^�����̘a��0�ł��邱�Ƃ����g���܂���B���ꂾ���Ȃ璼���I�ɖ��炩�Ȃ̂ŁA�����Ȃ蒼���I�ɉ����߂邱�Ƃ��ł���ł��傤�B�������A�������ǂ����邩�Ƃ����ۑ�͎c��܂��B
......[��]���ǂ��̖��������̂ɂ́A�ՓˑO�̑��x������t�������^�����̘a��0�ł��邱�Ƃ����g���܂���B���ꂾ���Ȃ璼���I�ɖ��炩�Ȃ̂ŁA�����Ȃ蒼���I�ɉ����߂邱�Ƃ��ł���ł��傤�B�������A�������ǂ����邩�Ƃ����ۑ�͎c��܂��B
�V(1) �Փ����P�CQ�����x��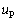 �C
�C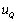 �Ƃ��܂��B
�Ƃ��܂��B 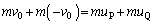 �@��
�@�� 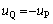
�����W���̎��F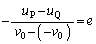
�� 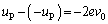 �@��
�@�� 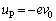 �����ŁA�������ʒu�G�l���M�[���l���Ă݂܂��B
�����ŁA�������ʒu�G�l���M�[���l���Ă݂܂��B
�o�l�萔k�̃o�l�ɕ��̂����āA���R��������L�яk����x�̂Ƃ����e�����ɂ���ʒu�G�l���M�[�́A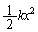 �ŗ^�����܂��B
�ŗ^�����܂��B
���̖��ł��A���SO������ψ���x�Ƃ��āAx���o�l���L���ƍl����A�����̂��n����������́A�o�l�Ɏ��t����ꂽ���̂��o�l������e�����Ɠ����`�����Ă��܂��B�o�l�萔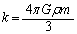 �̃o�l�ɂ���e���G�l���M�[���l���邱�Ƃɂ��A���Wx�̈ʒu�ɂ���A����m�̏������ʒu�G�l���M�[���A
�̃o�l�ɂ���e���G�l���M�[���l���邱�Ƃɂ��A���Wx�̈ʒu�ɂ���A����m�̏������ʒu�G�l���M�[���A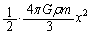 �ƍl���܂��B�����@�n���̓����ł́A�����ɑ������̈ˑ��̎d�����n���O�ƈႤ�̂ŁA�n���O�ł����L�����ɂ���ʒu�G�l���M�[�̌���
�ƍl���܂��B�����@�n���̓����ł́A�����ɑ������̈ˑ��̎d�����n���O�ƈႤ�̂ŁA�n���O�ł����L�����ɂ���ʒu�G�l���M�[�̌���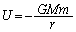 �͎g���܂���BC�_�ɂ�����P���͊w�I�G�l���M�[�́A�^���G�l���M�[
�͎g���܂���BC�_�ɂ�����P���͊w�I�G�l���M�[�́A�^���G�l���M�[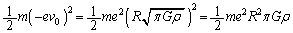 �ƁA�ʒu�G�l���M�[
�ƁA�ʒu�G�l���M�[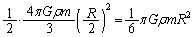 �̘a�ł��BD�_�ɂ�����P���͊w�I�G�l���M�[�́A�U���[���^���G�l���M�[��0�Ȃ̂ŁA�ʒu�G�l���M�[
�̘a�ł��BD�_�ɂ�����P���͊w�I�G�l���M�[�́A�U���[���^���G�l���M�[��0�Ȃ̂ŁA�ʒu�G�l���M�[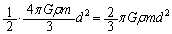 �݂̂ł��BC�_��D�_�Ƃ��͊w�I�G�l���M�[�ۑ����A
�݂̂ł��BC�_��D�_�Ƃ��͊w�I�G�l���M�[�ۑ����A �� 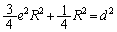 ��
�� 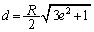 ......[��]
......[��]
d��P�̍s���P�U�����U���ł��B
(2) �Փˌ�����҂̉^�����P�U���ł��BP��Q�̒P�U���́A�U�����SO�Ɋւ����Ώ̂ȉ^���ɂȂ�܂��B
���̗��R���l���Ă݂܂��BQ�̏Փ˒�����^���G�l���M�[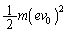 �́AP���^���G�l���M�[�Ɠ����ł��B�ʒu�G�l���M�[��P�Ɠ����Ȃ̂ŁAQ�̗͊w�I�G�l���M�[��P���͊w�I�G�l���M�[�Ɠ����ł��B�Ƃ������Ƃ́AQ��P�Ɠ��l�ɁA�U��d�̒P�U�������܂��BP�CQ�Ƃ�������T�ł��B
�́AP���^���G�l���M�[�Ɠ����ł��B�ʒu�G�l���M�[��P�Ɠ����Ȃ̂ŁAQ�̗͊w�I�G�l���M�[��P���͊w�I�G�l���M�[�Ɠ����ł��B�Ƃ������Ƃ́AQ��P�Ɠ��l�ɁA�U��d�̒P�U�������܂��BP�CQ�Ƃ�������T�ł��B
�Փˌ�AQ�́A���SO��ʉ߂���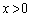 �ɓ���A
�ɓ���A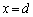 �܂ōs���Đ܂�Ԃ��Ă��܂��BP�́AD�_�Ő܂�Ԃ��A���SO��ʉ߂���
�܂ōs���Đ܂�Ԃ��Ă��܂��BP�́AD�_�Ő܂�Ԃ��A���SO��ʉ߂���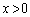 �ɓ���A�܂�Ԃ��Ă���Q�ƏՓ˂��܂��BC�_�ŏՓ˂����ȍ~�̉^���́AC�_�ŏՓ˂���܂ł̗��҂̉^�����A���傤�ǎ��v�̐j���t�ɂ����悤�ȉ^���ɂȂ�܂��B
�ɓ���A�܂�Ԃ��Ă���Q�ƏՓ˂��܂��BC�_�ŏՓ˂����ȍ~�̉^���́AC�_�ŏՓ˂���܂ł̗��҂̉^�����A���傤�ǎ��v�̐j���t�ɂ����悤�ȉ^���ɂȂ�܂��B
�Ƃ����킯�ŁA2��ڂ̏Փ˒n�_�́AC�_�̒��SO�Ɋւ����Ώ̓_E(OA�̒��_�ŁA���S�����������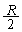 �ł���_)�ɂȂ�܂��BOA�̒��_ ......[��]���𗧂ĂĂ��ł��Ȃ��͂Ȃ��ł����A�ώG�Ȃ����Ȃ̂ŁA�^���̑Ώ̐��𗘗p���Đ�������̂��悢�ł��傤�B
�ł���_)�ɂȂ�܂��BOA�̒��_ ......[��]���𗧂ĂĂ��ł��Ȃ��͂Ȃ��ł����A�ώG�Ȃ����Ȃ̂ŁA�^���̑Ώ̐��𗘗p���Đ�������̂��悢�ł��傤�B
(3) 1��ڂ̏Փ˒n�_�͒��SO�ƒn�\�̓_B�̒��_C�ł��B2��ڂ̏Փ˒n�_�͒��SO�ƒn�\�̓_A�̒��_E�ł��B�Փ˒n�_�́A���̌�A���x�Փ˂��Ă��ς�邱�Ƃ͂���܂���B�܂��A�o�l�萔k������m�͕ω����Ȃ��̂ŁA�P�U�����������ω�����T�̂܂܂ł��B
�Փ˂��邲�ƂɁA������e�{����܂��B����ɔ����^���G�l���M�[��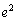 �{�ƂȂ茸�����܂��B�������A�Փ˒n�_���ς��Ȃ��̂ŁA�Փ˒��O������ʒu�G�l���M�[�͖���ς��܂���B�Փ˂��邲�Ƃ��^���G�l���M�[�������������āAn��Փˌ�ɁA�ŏ���
�{�ƂȂ茸�����܂��B�������A�Փ˒n�_���ς��Ȃ��̂ŁA�Փ˒��O������ʒu�G�l���M�[�͖���ς��܂���B�Փ˂��邲�Ƃ��^���G�l���M�[�������������āAn��Փˌ�ɁA�ŏ���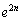 �{�ɂȂ��Ă��܂��B�\�����Ԃ��o�߂���ƁA
�{�ɂȂ��Ă��܂��B�\�����Ԃ��o�߂���ƁA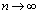 �Ƃ��āA
�Ƃ��āA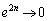 �ƂȂ�̂ŁA�ŏI�I�ɂ͏Փ˒��O������^���G�l���M�[��0�ɂȂ�܂��B����́A�P�U�����p�U���[��C��E�ł���A��̏�������̂ƂȂ��ĉ^�����邱�Ƃ��Ӗ����܂��B�]���āA�\���Ɏ��Ԃ��o�߂���ƁAP��Q�́A
�ƂȂ�̂ŁA�ŏI�I�ɂ͏Փ˒��O������^���G�l���M�[��0�ɂȂ�܂��B����́A�P�U�����p�U���[��C��E�ł���A��̏�������̂ƂȂ��ĉ^�����邱�Ƃ��Ӗ����܂��B�]���āA�\���Ɏ��Ԃ��o�߂���ƁAP��Q�́A
��̂ƂȂ���OA�COB�̒��_��U���[�Ƃ���P�U��(�U����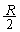 �C������T)���s���B ......[��]
�C������T)���s���B ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B