東大物理'20年前期[1]
xy平面内で運動する質量mの小球を考える。小球の各時刻における位置、速度、加速度、および小球にはたらく力のベクトルをそれぞれ
とする。また小球の各時刻における原点Oからの距離を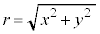 ,速度の大きさを
,速度の大きさを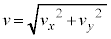 とする。以下の設問に答えよ。なお小球の大きさは無視できるものとする。
とする。以下の設問に答えよ。なお小球の大きさは無視できるものとする。
Ⅰ(1) 以下の文中の から
から に当てはまるものを
に当てはまるものを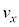 ,
,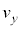 ,
,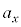 ,
,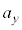 から選べ。
から選べ。 各時刻において原点Oと小球を結ぶ線分が描く面積速度は
で与えられる。ある時刻における位置および速度ベクトルが
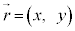 ,
,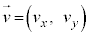
であったとき、それらは微小時間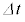 たった後にそれぞれ
たった後にそれぞれ 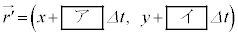 ,
,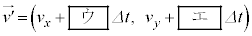
に変化する。このことを用いると、微小時間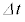 における面積速度の変化分は
における面積速度の変化分は で与えられる。なお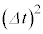 に比例した面積速度の変化分は無視する。
に比例した面積速度の変化分は無視する。
(2) 設問Ⅰ(1)の結果を用いて、面積速度が時間変化しないためには力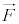 の成分
の成分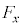 ,
,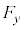 がどのような条件を満たせばよいか答えよ。ただし小球は原点Oから離れた点にあり、力は零ベクトルではないとする。
がどのような条件を満たせばよいか答えよ。ただし小球は原点Oから離れた点にあり、力は零ベクトルではないとする。
 (3) 設問Ⅰ(2)の力
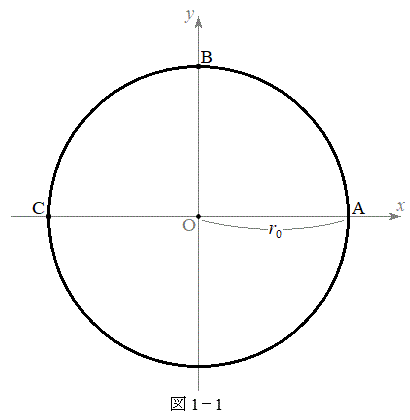
(3) 設問Ⅰ(2)の力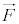 を受けながら、小球が図1-1の半径
を受けながら、小球が図1-1の半径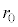 の円周上を点Aから点Bを通って点Cまで運動したとする。このとき、力
の円周上を点Aから点Bを通って点Cまで運動したとする。このとき、力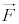 が点Aから点Bまでに小球に行う仕事と点Aから点Cまでに小球に行う仕事の大小関係を、理由を含めて答えよ。
が点Aから点Bまでに小球に行う仕事と点Aから点Cまでに小球に行う仕事の大小関係を、理由を含めて答えよ。
Ⅱ(1) 小球の原点Oからの距離rの時間変化率は
で与えられる。これを動径方向速度とよぶ。このとき、小球の運動エネルギーと
との差をm,rおよび面積速度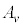 を用いた式で表せ。
を用いた式で表せ。
(2) 面積速度が一定になる力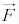 の例として万有引力を考える。原点Oに質量Mの物体があるとする。このとき万有引力による小球の位置エネルギーは
の例として万有引力を考える。原点Oに質量Mの物体があるとする。このとき万有引力による小球の位置エネルギーは 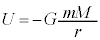 (式1)
(式1)で与えられる(Gは万有引力定数)。ただし物体の質量Mは小球の質量mと比べてはるかに大きいため、物体は原点Oに静止していると考えてよい。小球の面積速度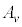 が0でないある定数値
が0でないある定数値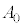 をとるとき、力学的エネルギーが最小となる運動はどのような運動になるか答えよ。また、そのときの力学的エネルギーの値をm,M,
をとるとき、力学的エネルギーが最小となる運動はどのような運動になるか答えよ。また、そのときの力学的エネルギーの値をm,M,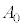 ,Gを用いて表せ。
,Gを用いて表せ。
Ⅲ ボーアの原子模型では電子の円軌道の円周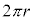 とド・ブロイ波長λの間に量子条件
とド・ブロイ波長λの間に量子条件 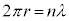 (
( )
)が成り立つ。以下で考える小球の円運動に対しても同じ量子条件が成り立つと仮定する。
(1) 設問Ⅱ(2)の(式1)に対応する万有引力がはたらく小球の円運動を考える。各nについて、量子条件を満たす円軌道の半径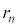 をn,h,m,M,Gを用いた式で表せ。ただし小球のド・ブロイ波長λは、小球の速度の大きさvを用いて
をn,h,m,M,Gを用いた式で表せ。ただし小球のド・ブロイ波長λは、小球の速度の大きさvを用いて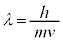 で与えられる(hはプランク定数)。
で与えられる(hはプランク定数)。
(2) 宇宙には暗黒物質という物質が存在し、銀河の暗黒物質は銀河中心からおよそ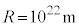 の半径内に集まっていると考えられている。暗黒物質が未知の粒子によって構成されていると仮定し、設問Ⅲ(1)の結果を用いてその粒子の質量に下限を与えてみよう。暗黒物質の構成粒子を、(式1)に対応する万有引力を受けながら円運動する小球として近似する。設問Ⅲ(1)で考えたボーアの量子条件を満たす小球の軌道半径のうち
の半径内に集まっていると考えられている。暗黒物質が未知の粒子によって構成されていると仮定し、設問Ⅲ(1)の結果を用いてその粒子の質量に下限を与えてみよう。暗黒物質の構成粒子を、(式1)に対応する万有引力を受けながら円運動する小球として近似する。設問Ⅲ(1)で考えたボーアの量子条件を満たす小球の軌道半径のうち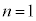 としたものが
としたものが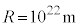 と等しいとしたときの小球の質量を求めよ。
と等しいとしたときの小球の質量を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 問題の最後では最近話題の暗黒物質(ダークマター)まで扱うという壮大なスケールの問題ですが、親切な誘導に乗って言われた通りに計算していけばゴールにたどり着ける円運動の問題です。
Ⅰ(1) ある時刻に位置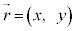 ,速度
,速度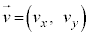 ,加速度
,加速度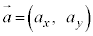 (変位・速度・加速度を参照),面積速度
(変位・速度・加速度を参照),面積速度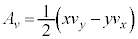 ・・・① (
・・・① (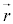 と
と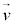 で作る平行四辺形の面積の
で作る平行四辺形の面積の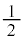 )であったとき、微小時間
)であったとき、微小時間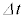 後、位置
後、位置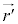 ,速度
,速度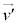 は、
は、 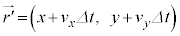 , (ア)
, (ア) 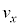 (イ)
(イ) 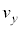 ......[答]
......[答]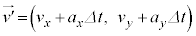 , (ウ)
, (ウ) 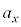 (エ)
(エ) 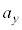 ......[答]
......[答]面積速度の変化分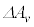 は、
は、 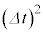 を無視すると、
を無視すると、
②より、
面積速度が変化しないので、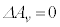 より、
より、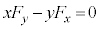 ......[答]この条件は、
......[答]この条件は、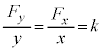 とおくと、
とおくと、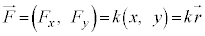 より、
より、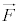 //
// 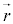 を意味します。
を意味します。
(3) 円周上を運動する点の速度は円の接線方向を向くので、速度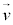 と位置ベクトル
と位置ベクトル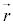 とは垂直になります。(2)より、
とは垂直になります。(2)より、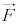 //
// 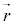 なので、力
なので、力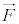 は、速度
は、速度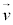 と垂直で仕事をしません。力
と垂直で仕事をしません。力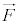 が点Aから点Bまでに小球に行う仕事と、点Aから点Cまでに小球に行う仕事は、ともに0で等しくなります。 ......[答]
が点Aから点Bまでに小球に行う仕事と、点Aから点Cまでに小球に行う仕事は、ともに0で等しくなります。 ......[答]
Ⅱ(1) 問題文のrの時間変化率の式は、極座標と直交座標の変換公式から以下のようにして導けます。 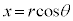 ,
,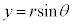
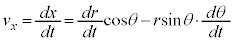 ・・・③
・・・③
 ・・・④
・・・④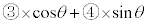 より、
より、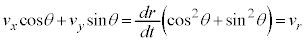 (小球の原点Oからの距離rの時間変化率は
(小球の原点Oからの距離rの時間変化率は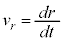 )
)rをかけて、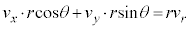 ,
,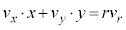 よって、
よって、 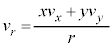 ・・・⑤
・・・⑤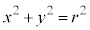 と①より、
と①より、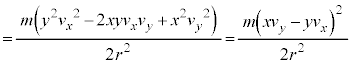
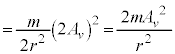 ......[答]
......[答]これより、小球の運動エネルギーは、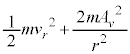 ・・・⑥ となります。
・・・⑥ となります。
(2) 小球の面積速度が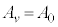 (一定)となるとき、小球の力学的エネルギーEは、(1)の結果と(式1)とから、
(一定)となるとき、小球の力学的エネルギーEは、(1)の結果と(式1)とから、 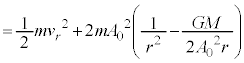
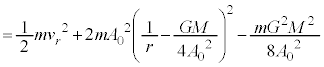 ・・・⑦
・・・⑦Eは、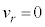 かつ
かつ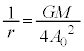 のとき最小(2次関数の最大最小を参照)となり、このとき、
のとき最小(2次関数の最大最小を参照)となり、このとき、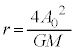 ( = 一定)より、運動は円運動で、さらに、このとき⑥で
( = 一定)より、運動は円運動で、さらに、このとき⑥で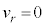 ,
,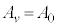 とすることにより運動エネルギーは、
とすることにより運動エネルギーは、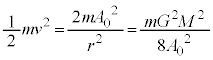 より、
より、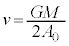 (= 一定),従って、力学的エネルギーが最小となる運動は、等速円運動 ......[答]⑦の力学的エネルギーEは、
(= 一定),従って、力学的エネルギーが最小となる運動は、等速円運動 ......[答]⑦の力学的エネルギーEは、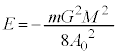 .......[答]
.......[答]
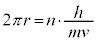 ・・・⑧
・・・⑧Ⅱ(2)の円運動として考えるので、小球の運動方程式: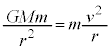 より、
より、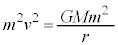 、
、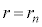 として、
として、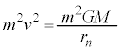
⑧より、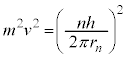
よって、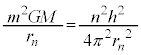 ∴
∴ 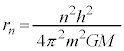 ......[答]
......[答] (2) (1)の結果より、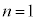 ,
,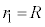 として、
として、 よって、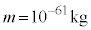 ......[答]
......[答]
注.暗黒物質について
銀河系の回転速度をドップラー効果の利用により観測すると、銀河の周辺に行くに従って万有引力が弱くなり遅くなりそうなものなのに、あまり変化しない、という結果が得られています。これを説明するためには、周辺部にある程度の質量が存在している必要があるのですが、銀河系周辺部の光の強さを調べると、その質量分の光量がなく、見えない(光っていない)質量が存在するのだろう、と言われています。この見えない質量分の物質を暗黒物質と言います(銀河規模になるとニュートン力学が破綻し、別の理論に従う、という意見もあります)。
アインシュタインの相対性理論によると、大きな重力を作る物体の周辺を光が通過するとき光の進路が物体側に屈曲することが知られています。この効果はレンズによる屈折と似ているので、重力レンズと呼ばれており、大きな質量をもつ銀河系の向こう側にあって見えないはずの天体が見えたり、まるでレンズを通して見ているように観測される天体が存在することからその実在が確かめられています。宇宙には、光っている天体以外にも、重力レンズの効果が確認できる部分があるので、ここからも暗黒物質の存在が確認できます。
暗黒物質の実体は何か、という問いの答はまだ出ていません。ニュートリノ(長らく、ニュートリノには質量がないと言われていましたが、1998年にニュートリノ振動という現象が発見され、僅かだが質量を持つことが証明された)、ブラックホール、ニュートラリーノ・アキシオンなどの未知の素粒子、いろいろな候補があがっています。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大物理TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 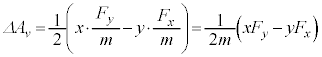
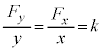 とおくと、
とおくと、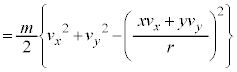
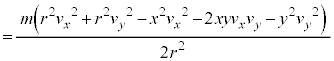
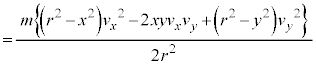
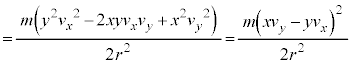
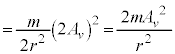 ......[答]
......[答]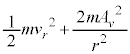 ・・・⑥ となります。
・・・⑥ となります。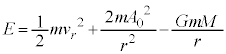
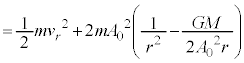
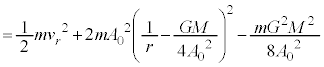 ・・・⑦
・・・⑦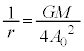 のとき最小(2次関数の最大最小を参照)となり、このとき、
のとき最小(2次関数の最大最小を参照)となり、このとき、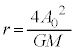 ( = 一定)より、運動は円運動で、さらに、このとき⑥で
( = 一定)より、運動は円運動で、さらに、このとき⑥で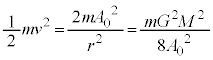 より、
より、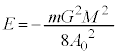 .......[答]
.......[答]