行列


【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
 【広告】広告はここまでです。
電子回路の解析から、気象予報、経済予測に至るまで、行列は、計算機に様々な仕事をさせるための道具です。ここでは、行列の基本的な計算から、連立1次方程式や1次変換への応用、行列の累乗計算の技巧などを扱います。

ここで学習する内容は、以下の通りです。各項目をクリックしてください。

行列　行列に関する基本事項、行列の和、差、相等、実数倍について触れます。
行列の積　行列の積の計算法を学びます。行列の積では、交換法則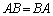が成り立ちません。
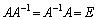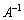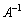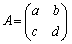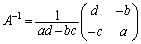逆行列　(E：単位行列)を満たす行列が逆行列です。逆行列の求め方を学びます。2次の正方行列では、となります。係数の分母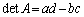を行列式と言います。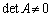のときにのみ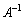が存在します。
行列と連立1次方程式　行列を用いて連立1次方程式を記述すると、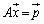となります。この解は、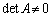のときには、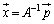となります。
基本変形　連立1次方程式を解くときの操作を行列を用いて考察します。この考察により、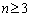のときのn次正方行列の逆行列の求め方が明らかになります。
固有値・固有ベクトル　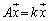 (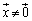)を満たす実数kを行列Aの固有値、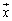を行列Aの固有ベクトルと言います。固有値kは固有方程式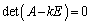の解です。2次の正方行列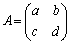の固有方程式は、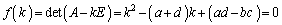となります。
ハミルトン・ケーリーの定理　行列Aの固有方程式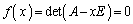：のxを行列Aに代えた式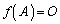：が成立します。2次の正方行列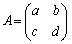においては、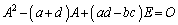が成立します。
1次変換　ベク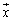トルをベクトル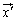に対応させる変換f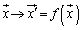：において、2つのベクトル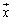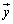，について、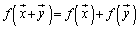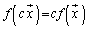，が成り立つとき、fを1次変換と言います。1次変換は行列を用いて記述できます。
1次変換(その2)　原点を通る直線に関する対称移動、回転移動を表す行列を考察します。
行列の対角化　行列Aの固有ベクトルを列ベクトルとして横に並べてできる行列をPとして、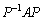は固有値を対角成分とし、他の成分は0となる行列となります。この操作を行列の対角化と言います。
スペクトル分解　任意のベクトルについて、行列Aの固有値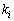に対応する固有ベクトルの方向成分を取り出す1次変換を射影と言います。射影の表現行列を射影子と言い、固有値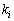に対応する射影子を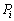とすると、n次正方行列Aが異なるn個の固有値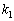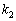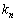，，･･･，をもつときには、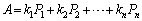という形に書くことができます。Aが対称行列の場合(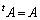)にこの形をスペクトル分解と言います。
行列の累乗　行列の対角化、スペクトル分解、ハミルトン・ケーリーの定理などを応用して行列の累乗を求める種々の技巧を考察します。


【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
 【広告】広告はここまでです。
　　数学基礎事項TOP　　数学TOP　　TOPページに戻る

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。
©2005-2024
(有)りるらる
苦学楽学塾 随時入会受付中！
理系大学受験ネット塾苦学楽学塾
(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。