���k�啨��'08�N�O��[2]
�[�d���ꂽ�R���f���T�[�ɒ�R��R�C�����Ȃ��ŕ��d������ƁA�R���f���T�[�ɒ~�����Ă����G�l���M�[�́A��R�ɂ���Đ�����M��R�C�������鎥��̃G�l���M�[�ɕω�����B�����ł́A�R���f���T�[A(�d�C�e��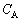 )�C�R���f���T�[B(�d�C�e��
)�C�R���f���T�[B(�d�C�e��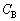 )�C��R(�d�C��RR)�A�R�C��(���ȃC���_�N�^���XL)�A�����d��(�d��
)�C��R(�d�C��RR)�A�R�C��(���ȃC���_�N�^���XL)�A�����d��(�d��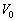 )���܂މ�H���l���A��R�ƃR�C���̓������r����B�d���̓�����R��A��H�̓�������уR�C���̓d�C��R�͖����ł�����̂Ƃ���B�܂��A�d���g�̕��˂͍l���Ȃ��Ă悢�B���̂Ƃ��A�ȉ��̖₢�ɓ�����B�܂��A���ʂ����łȂ��A�l������v�Z�̉ߒ����L���B
)���܂މ�H���l���A��R�ƃR�C���̓������r����B�d���̓�����R��A��H�̓�������уR�C���̓d�C��R�͖����ł�����̂Ƃ���B�܂��A�d���g�̕��˂͍l���Ȃ��Ă悢�B���̂Ƃ��A�ȉ��̖₢�ɓ�����B�܂��A���ʂ����łȂ��A�l������v�Z�̉ߒ����L���B
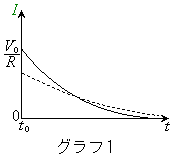
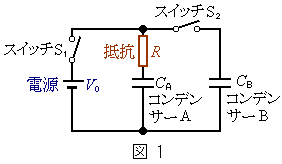 ��1�@�}1�Ɏ�����H���l����B������ԂŃX�C�b�`
��1�@�}1�Ɏ�����H���l����B������ԂŃX�C�b�`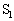 �C
�C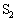 �͊J���Ă���A�R���f���T�[A�CB�ɓd�ׂ͒~�����Ă��Ȃ������B
�͊J���Ă���A�R���f���T�[A�CB�ɓd�ׂ͒~�����Ă��Ȃ������B(a) ����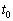 �ɂ����ăX�C�b�`
�ɂ����ăX�C�b�`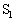 ����A�R���f���T�[A�̏[�d���J�n�����B��R�𗬂��d��I�̎��ԕω��̂����悻�̌`���A����
����A�R���f���T�[A�̏[�d���J�n�����B��R�𗬂��d��I�̎��ԕω��̂����悻�̌`���A����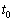 ���[�d���قڊ�������܂ł͈̔͂ŃO���t1�Ɏ����ŕ`���B�܂��A����
���[�d���قڊ�������܂ł͈̔͂ŃO���t1�Ɏ����ŕ`���B�܂��A����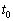 �ł̓d���̑傫����
�ł̓d���̑傫����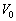 �CR��p���ďc���ɋL���B
�CR��p���ďc���ɋL���B (b) ��1(a)�ɂ����ēd�C��R�l��R���傫�Ȓ�R��p�����ꍇ�A�d��I�̎��ԕω��ɂ͂ǂ̂悤�ȈႢ������邩�B�d���̎��ԕω��̂����悻�̌`���1(a)�Ɣ�r�ł���悤�ɃO���t1�ɔj���ŕ`���B
(c) ��1(a)�ɂ����ăR���f���T�[A�̏[�d������������A�X�C�b�`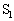 ���J���Ă���X�C�b�`
���J���Ă���X�C�b�`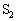 ������B���̌�A�\���Ɏ��Ԃ��o�߂����Ƃ��̃R���f���T�[A�̓d�C��
������B���̌�A�\���Ɏ��Ԃ��o�߂����Ƃ��̃R���f���T�[A�̓d�C��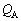 �ƁA�R���f���T�[B�̓d�C��
�ƁA�R���f���T�[B�̓d�C��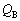 ���A���ꂼ��A
���A���ꂼ��A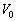 �C
�C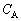 �C
�C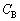 �CR�̒�����K�v�Ȃ��̂�p���ĕ\���B
�CR�̒�����K�v�Ȃ��̂�p���ĕ\���B 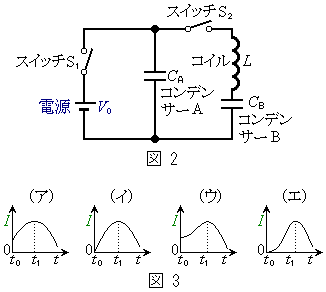 ��2�@���ɁA�R�C�����܂ސ}2�Ɏ�����H���l����B������ԂŃX�C�b�`
��2�@���ɁA�R�C�����܂ސ}2�Ɏ�����H���l����B������ԂŃX�C�b�`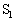 �C
�C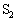 �͊J���Ă���A�R���f���T�[A�CB�ɂ͓d�ׂ͒~�����Ă��Ȃ������B
�͊J���Ă���A�R���f���T�[A�CB�ɂ͓d�ׂ͒~�����Ă��Ȃ������B(a) �X�C�b�`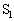 ����ăR���f���T�[A���[�d������A�X�C�b�`
����ăR���f���T�[A���[�d������A�X�C�b�`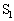 ���J�����B���̌�A����
���J�����B���̌�A����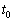 �ɂ����ăX�C�b�`
�ɂ����ăX�C�b�`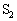 ������Ƃ���A�R�C���ɓd�������ꂽ�B���̌�A�d���͎���
������Ƃ���A�R�C���ɓd�������ꂽ�B���̌�A�d���͎���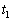 �ōő�l���Ƃ�A�����ɓ]�����B�d��I�̎��ԕω���\���O���t�Ƃ��Đ������ƍl��������̂��A�}3��(�A)�`(�G)�̒������I�сA�L���œ�����B�܂��A����
�ōő�l���Ƃ�A�����ɓ]�����B�d��I�̎��ԕω���\���O���t�Ƃ��Đ������ƍl��������̂��A�}3��(�A)�`(�G)�̒������I�сA�L���œ�����B�܂��A����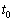 �ɂ�����d��I�̒l�Ƃ��̎��ԕω��ɗ��ӂ��āA���R���L���B
�ɂ�����d��I�̒l�Ƃ��̎��ԕω��ɗ��ӂ��āA���R���L���B (b) ����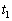 �ɂ����āA�R���f���T�[A�C�R���f���T�[B�ɂ����邻�ꂼ��̓d��
�ɂ����āA�R���f���T�[A�C�R���f���T�[B�ɂ����邻�ꂼ��̓d��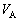 �C
�C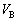 ��
��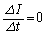 �ł��邱�Ƃ��l�����ċ��߁A������
�ł��邱�Ƃ��l�����ċ��߁A������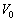 �C
�C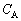 �C
�C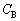 �CL�̒�����K�v�Ȃ��̂�p���ĕ\���B
�CL�̒�����K�v�Ȃ��̂�p���ĕ\���B (c) ����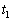 �ɂ����āA�R���f���T�[B�ɒ~�����Ă���G�l���M�[
�ɂ����āA�R���f���T�[B�ɒ~�����Ă���G�l���M�[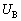 �ƃR�C���ɒ~�����Ă���G�l���M�[
�ƃR�C���ɒ~�����Ă���G�l���M�[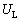 ���A���ꂼ��A
���A���ꂼ��A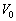 �C
�C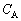 �C
�C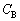 �CL�̒�����K�v�Ȃ��̂�p���ĕ\���B
�CL�̒�����K�v�Ȃ��̂�p���ĕ\���B (d) ����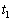 �ȍ~�ɂ����ēd��I���ŏ���0�ɂȂ��������ɃX�C�b�`
�ȍ~�ɂ����ēd��I���ŏ���0�ɂȂ��������ɃX�C�b�`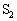 ���J�����B���̂Ƃ��A�R���f���T�[B�ɒ~�����Ă����d�C��
���J�����B���̂Ƃ��A�R���f���T�[B�ɒ~�����Ă����d�C��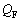 ���A
���A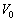 �C
�C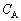 �C
�C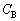 �CL�̒�����K�v�Ȃ��̂�p���ĕ\���B
�CL�̒�����K�v�Ȃ��̂�p���ĕ\���B (e) ���̈�A�̑���ŁA�[�d�ɂ���Ē~����ꂽ�R���f���T�[A�̃G�l���M�[�����ׂăR���f���T�[B�Ɉڂ����߂ɕK�v��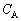 ��
��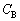 �̊Ԃ̊W�������߂�B
�̊Ԃ̊W�������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��R�ƃR�C�����r���Ă���̂ł����A�Ȃ��Ȃ������[�����ł��B
��1�̍ŏ��́A�����������Ȃǂ������K�v�͂���܂���B���Ԃ̃��_�ł��B�u�R���f���T�[�́A�X�C�b�`��ւ�����ɓ��ʂ����̂Ɠ��l�̓�����s���A�[�������o�߂��ď[�d���������Ă��܂����d���𗬂��Ȃ��B�R�C���́A�X�C�b�`��ւ�������d���𗬂����A�[�������o�߂���ƒP�Ȃ铱���Ƃ��ē��삷��B�܂��A���̊Ԃ͎w�����I�ȕω����s���B�v�Ƃ�����b����(�R���f���T�[�̉ߓn�����A�R�C���̉ߓn�������Q��)��m���Ă���悢�̂ł��B
 ��1(a) �X�C�b�`
��1(a) �X�C�b�`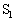 ���������́A�R���f���T�[�͓��ʂ����̂Ɠ��l�̓�����s���܂��B�I�[���̖@�����A����
���������́A�R���f���T�[�͓��ʂ����̂Ɠ��l�̓�����s���܂��B�I�[���̖@�����A����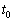 �ɂ������d����
�ɂ������d����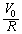 �ł��B�[�d���قڊ���������d����0�ɋ߂Â��Ă����܂��B���̊Ԃ͎w�����I�ɕω����A�d��I�������ω��͉E�}�O���t1�̎����̂悤�ɂȂ�܂��B
�ł��B�[�d���قڊ���������d����0�ɋ߂Â��Ă����܂��B���̊Ԃ͎w�����I�ɕω����A�d��I�������ω��͉E�}�O���t1�̎����̂悤�ɂȂ�܂��B(b) ����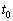 �ɂ������d������RR�̏ꍇ�����������Ȃ�܂��B���̌�̓R���f���T�[�ɗ��ꍞ���d�������Ȃ��̂ŁA�[�d�����܂ł�������������悤�ɂȂ�܂��B���̂��Ƃ����ĂɂȂ�悤�ɁAR�����傫����R��p�����ꍇ���d���ω��̃O���t�́A(a)�̎����Ɠr���Ō����悤�ɕ`�����Ƃɂ��A�E�}�O���t1�̔j���̂悤�ɂȂ�܂��B
�ɂ������d������RR�̏ꍇ�����������Ȃ�܂��B���̌�̓R���f���T�[�ɗ��ꍞ���d�������Ȃ��̂ŁA�[�d�����܂ł�������������悤�ɂȂ�܂��B���̂��Ƃ����ĂɂȂ�悤�ɁAR�����傫����R��p�����ꍇ���d���ω��̃O���t�́A(a)�̎����Ɠr���Ō����悤�ɕ`�����Ƃɂ��A�E�}�O���t1�̔j���̂悤�ɂȂ�܂��B (c) �[�����������o�߂���ƁA��R�𗬂���d����0�ƂȂ�A��R���d����0�ɂȂ�܂��B���̂Ƃ��A�R���f���T�[A�CB�́A���[���d�����������Ȃ����ڑ�����Ă���̂Ɠ��l�ł����āA�����e����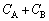 �ł��B
�ł��B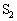 ���ւ���O��A���d��
���ւ���O��A���d��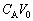 ��~���Ă����̂ŁAA�CB���[���d��
��~���Ă����̂ŁAA�CB���[���d��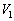 �́A
�́A 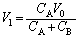 �@����@
�@����@����āAA�CB���~���Ă����d�C��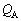 �C
�C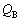 �́A
�́A 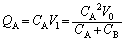 �C
�C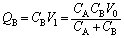 ......[��]
......[��]�[�����������o�߂���ƁAA�CB���G�l���M�[�̘a�́A�@��p���āA
�W���[���M�Ƃ��čŏI�I�Ɏ������G�l���M�[�̑傫��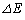 �́A
�́A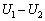 �ɓ������A
�ɓ������A 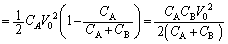 ......[��]
......[��]
��2(a) ����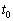 �ɂ����ẮA�X�C�b�`
�ɂ����ẮA�X�C�b�`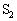 ��ւ�����̂��߁A�R�C�����d���𗬂����A
��ւ�����̂��߁A�R�C�����d���𗬂����A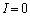 �ł��B���̎��_�ł́A�R���f���T�[B�ɂ��d�����~�����Ă��Ȃ����߁AB���[���d����0�ł��B�R���f���T�[A���[���d����
�ł��B���̎��_�ł́A�R���f���T�[B�ɂ��d�����~�����Ă��Ȃ����߁AB���[���d����0�ł��B�R���f���T�[A���[���d����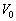 �C�R�C�����[���d����
�C�R�C�����[���d����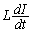 (���ȗU�����Q��)�Ȃ̂ŁA
(���ȗU�����Q��)�Ȃ̂ŁA 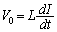 �@(B�̏㑤�̋ɔ����d�������ꍞ�ތ������d�����Ƃ��Ă��܂�)
�@(B�̏㑤�̋ɔ����d�������ꍞ�ތ������d�����Ƃ��Ă��܂�)�� 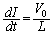 (
(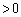 �C�܂�A�d��I�͑���)�]���āA����
�C�܂�A�d��I�͑���)�]���āA����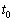 �ɂ����āA
�ɂ����āA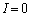 �ł���A�ڐ��̌X�������ł���悤�ȃO���t��I�т܂��B(�C) ......[��]���R�F����
�ł���A�ڐ��̌X�������ł���悤�ȃO���t��I�т܂��B(�C) ......[��]���R�F����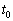 �ɂ����āA�R�C���̎��ȗU���̂��ߓd����0�ŁA�d���̕ω���
�ɂ����āA�R�C���̎��ȗU���̂��ߓd����0�ŁA�d���̕ω���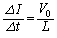 �͐�������B ......[��]
�͐�������B ......[��] ���DLC��H�Ȃ̂ŁA�P�U������̂��낤�A�Ƃ������ƂŁA�����g��(�C)�Ƃ��Ă��悢�����m��܂���B 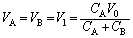 ......[��]�@����A
......[��]�@����A(c) B�ɒ~�����Ă����G�l���M�[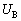 �́A
�́A 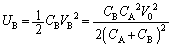 ......[��]
......[��]�R�C���ɒ~�����Ă����G�l���M�[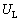 �́A��1(c)��
�́A��1(c)��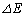 �ɓ������A
�ɓ������A 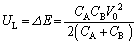 ......[��]
......[��](d) �������ł���A�P�U���ƌ��߂��āA����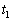 ��ɍŏ���
��ɍŏ���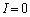 �ƂȂ����_(����
�ƂȂ����_(����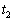 �Ƃ��܂��B����
�Ƃ��܂��B����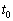 ����P�U������������)�ł́A�R�C�����[���d��������
����P�U������������)�ł́A�R�C�����[���d��������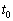 �ɂ������d���̕������t�ɂ�������
�ɂ������d���̕������t�ɂ�������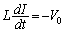 �Ƃ��Ă����āA�L���q�z�b�t�̑�2�@�����A
�Ƃ��Ă����āA�L���q�z�b�t�̑�2�@�����A 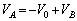 �@����B
�@����B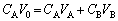 �@����C
�@����C�B�C�C��A�����āA
�� 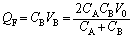 ......[��]�Ƃ��Ă��܂��̂��������Ǝv���܂��B�P�U�����ǂ����킩��Ȃ��A�Ƃ����O��ɗ��̂ł���A����
......[��]�Ƃ��Ă��܂��̂��������Ǝv���܂��B�P�U�����ǂ����킩��Ȃ��A�Ƃ����O��ɗ��̂ł���A����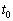 �ɂ������G�l���M�[�́A
�ɂ������G�l���M�[�́A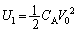 ����
����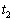 �ɂ����āA�d��0���R�C�����G�l���M�[��0 (���ȗU�����Q��)�ł����āAA�CB���G�l���M�[�́A
�ɂ����āA�d��0���R�C�����G�l���M�[��0 (���ȗU�����Q��)�ł����āAA�CB���G�l���M�[�́A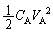 �C
�C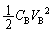 �C����ćB�̑���ɁA�G�l���M�[�ۑ����A
�C����ćB�̑���ɁA�G�l���M�[�ۑ����A 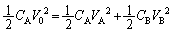 �@����D
�@����D�Ƃ��������ĂćC�ƘA�����܂��B�C���A
������D�ɑ�����邱�Ƃɂ��A
������Đ�������ƁA
�� 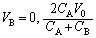
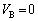 ������
������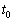 �ɂ�����B���d���Ȃ̂ŁA����
�ɂ�����B���d���Ȃ̂ŁA����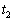 �ɂ������d���Ƃ��ẮA
�ɂ������d���Ƃ��ẮA 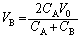
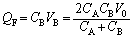 ......[��]
......[��]�ƂȂ�܂��B
(e) �B(���邢�͇C)���A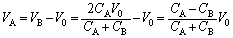
����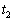 �ɂ�����A���~���Ă����d��
�ɂ�����A���~���Ă����d��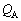 �́A
�́A A���~���Ă����G�l���M�[��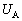 �́A
�́A �R���f���T�[A���G�l���M�[�����ׂăR���f���T�[B�Ɉڂ���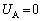 �ɂȂ�̂ŁA���̂��߂ɕK�v��
�ɂȂ�̂ŁA���̂��߂ɕK�v��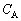 ��
��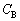 �̊Ԃ̊W���́A
�̊Ԃ̊W���́A 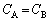 ......[��]
......[��]���D�R���f���T�[A�́u�G�l���M�[�v���ڂ��̂ł����āA�d�����ڂ��̂ł͂Ȃ����Ƃɒ��ӂ��Ă��������B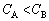 �̏ꍇ�A
�̏ꍇ�A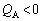 �ɂȂ蓾�܂����A���̂Ƃ��A�t��A���G�l���M�[��
�ɂȂ蓾�܂����A���̂Ƃ��A�t��A���G�l���M�[��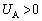 �ɂȂ��Ă��܂��܂��B
�ɂȂ��Ă��܂��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B