三角比・三角関数・指数関数・対数関数演習問題
京都府立大数学'09年[1]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
定数aを実数とし、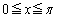 とする。関数
とする。関数
とする。以下の問いに答えよ。
(1)  とするとき、tの値の範囲を求めよ。
とするとき、tの値の範囲を求めよ。 (2) yをtの式で表せ。
(3) 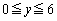 がつねに成り立つように、aの値の範囲を求めよ。
がつねに成り立つように、aの値の範囲を求めよ。 (4) 方程式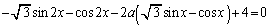 が3個以上の異なる実数解をもつように、aの値の範囲を求めよ。
が3個以上の異なる実数解をもつように、aの値の範囲を求めよ。 [解答へ]
首都大理系数学'08年前期[4]
以下の問いに答えよ。
(1) 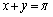 を満たす実数x,yに対して、次の等式が成り立つことを示せ。
を満たす実数x,yに対して、次の等式が成り立つことを示せ。 (2) 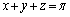 を満たす実数x,y,zに対して、次の等式が成り立つことを示せ。
を満たす実数x,y,zに対して、次の等式が成り立つことを示せ。 (3) 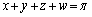 を満たす実数x,y,z,wに対して、等式
を満たす実数x,y,z,wに対して、等式 は必ずしも成り立たないことを示せ。
[解答へ]
慈恵医大数学'08年[2]
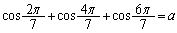 ,
,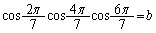
とする。aとbの値を求めたい。以下の設問(1),(2),(3)に答えよ。
(1) 角θ (ラジアン)が
をみたすとき、解のひとつが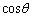 であるような4次の方程式を求めよ。
であるような4次の方程式を求めよ。 (2) 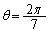 のとき、
のとき、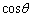 が解のひとつであるような3次の方程式を求めよ。
が解のひとつであるような3次の方程式を求めよ。 (3) 設問(2)の結果を用いて、aおよびbの値を求めよ。
[解答へ]
岩手大教育数学'09年[1]
次の問いに答えよ。
(1) 正弦と余弦の加法定理を用いて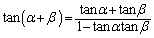 を示せ。
を示せ。 (2) 直角三角形ではない三角形の内角の大きさを、それぞれα,β,γとするとき、
の値は、α,β,γによらずに一定であることを示し、その値を求めよ。
(3) 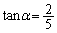 のとき、
のとき、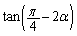 の値を求めよ。
の値を求めよ。 [解答へ]
首都大理系数学'09年前期[2]
以下の問いに答えよ
(1) 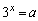 ,
,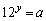 ,
,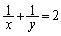 を満たす実数x,yが存在するようなaの値を求めよ。
を満たす実数x,yが存在するようなaの値を求めよ。 (2) 正の実数b,c,zが
を満たすとき、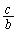 のとり得る値の範囲を求めよ。
のとり得る値の範囲を求めよ。 [解答へ]
九大文系数学'08年[4]
放物線C: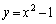 と
と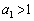 をみたす実数
をみたす実数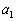 を考える。このとき、次の問いに答えよ。
を考える。このとき、次の問いに答えよ。
(1) C上の点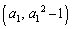 における接線とx軸との交点のx座標を
における接線とx軸との交点のx座標を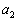 とするとき、
とするとき、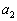 を
を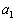 を用いて表せ。
を用いて表せ。 (2) (1)で求めた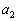 に対して、C上の点
に対して、C上の点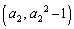 における接線とx軸との交点のx座標を
における接線とx軸との交点のx座標を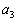 とする。この操作を繰り返してできる数列を
とする。この操作を繰り返してできる数列を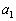 ,
,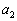 ,・・・,
,・・・,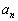 ,・・・とする。このとき、すべてのnに対して、
,・・・とする。このとき、すべてのnに対して、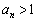 を示せ。
を示せ。 (3) 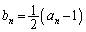 とおくとき、すべてのnに対して、
とおくとき、すべてのnに対して、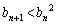 を示せ。
を示せ。 (4) 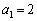 のとき、
のとき、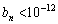 となるnの値を1つ求めよ。ただし、必要があれば、
となるnの値を1つ求めよ。ただし、必要があれば、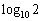 を
を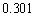 として計算してよい。
として計算してよい。 [解答へ]
名工大数学'10年前期[1]
四角形ABCDは次の条件を満たす。
(i) 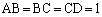
(ii) 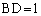 ,
,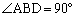
線分ACと線分BDの交点をEとする。線分ABを3等分して、点Aに近い分点をMとし、点Bに近い分点をNとする。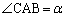 ,
,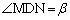 とおくとき、次の問いに答えよ。
とおくとき、次の問いに答えよ。
(1) 線分の長さの比の値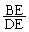 を求めよ。
を求めよ。 (2) 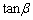 の値を求めよ。
の値を求めよ。 (3) αとβ の大小を判定せよ。
[解答へ]
九大数学'10年前期[1]
三角形ABCの3辺の長さを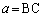 ,
,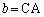 ,
,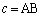 とする。実数
とする。実数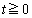 を与えたとき、Aを始点としBを通る半直線上に
を与えたとき、Aを始点としBを通る半直線上に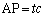 となるように点Pをとる。次の問いに答えよ。
となるように点Pをとる。次の問いに答えよ。
(1) 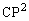 をa,b,c,tを用いて表せ。
をa,b,c,tを用いて表せ。 (2) 点Pが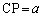 を満たすとき、tを求めよ。
を満たすとき、tを求めよ。 (3) (2)の条件を満たす点Pが辺AB上にちょうど2つあるとき、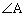 と
と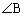 に関する条件を求めよ。
に関する条件を求めよ。 [解答へ]
広島大理系数学'10年後期[3]
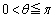 に対して
に対して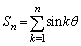 (
(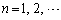 )を考える。以下の問いに答えよ。
)を考える。以下の問いに答えよ。
(1) 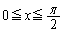 のとき、
のとき、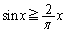 が成り立つことを示せ。
が成り立つことを示せ。 (2) 等式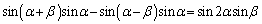 を示せ。
を示せ。 (3) 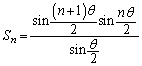 が成り立つことを示せ。
が成り立つことを示せ。 (4) 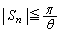 が成り立つことを示せ。
が成り立つことを示せ。 [解答へ]
群馬大医数学'10年[2]
(1) nを自然数とし、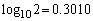 ,
,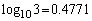 とする。
とする。 (ア) 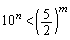 を満たす自然数mに対し、
を満たす自然数mに対し、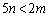 を証明せよ。
を証明せよ。 (イ) 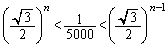 を満たすnを求めよ。
を満たすnを求めよ。 (2) 実数x,yが連立方程式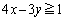 ,
,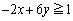 を満たすとき、
を満たすとき、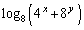 の最小値を求めよ。
の最小値を求めよ。 [解答へ]
早大教育数学'10年[3]
座標平面上で、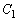 ,
,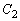 ,
,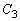 を、それぞれ、中心が
を、それぞれ、中心が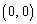 ,
,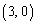 ,
,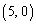 ,半径が2,1,1である円周とする。点Pは点
,半径が2,1,1である円周とする。点Pは点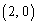 を出発点とし、円周
を出発点とし、円周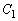 上を反時計回りに等速で
上を反時計回りに等速で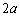 秒で一周する。点Qは点
秒で一周する。点Qは点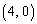 を出発点とし、まず円周
を出発点とし、まず円周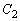 上を反時計回りに等速でa秒で一周し、続いて円周
上を反時計回りに等速でa秒で一周し、続いて円周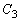 上を時計回りに等速でa秒で一周する。
上を時計回りに等速でa秒で一周する。
点P,Qが同時に出発するとき、線分PQの長さの最大値と最小値を求めよ。ただし、aは正の定数である。
[解答へ]
横浜国大理工数学'11年前期[2]
次の問いに答えよ。
(1) 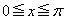 において、
において、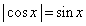 を満たすxを求め、
を満たすxを求め、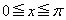 において、
において、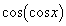 ,
,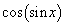 の大小を比較せよ。
の大小を比較せよ。 (2) 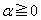 ,
,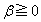 ,
,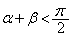 のとき、
のとき、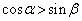 となることを示し、
となることを示し、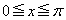 において、
において、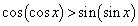 を示せ。
を示せ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 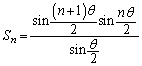 が成り立つことを示せ。
が成り立つことを示せ。