��啨��'21�N�O��[3]
�ȉ���A��B�̗����̖��ɉ���B�Ȃ�A��B�͓Ɨ��������e�̖��ł���B
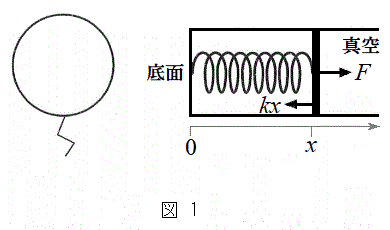 A�D�@��C���������S�����D(�}1��)�́A�O����͂��炭���͂�A���x�ɉ����āA�傫�����ς��B���̂ӂ�܂����A�ȉ��̂悤�ɒP�����������f���ōl���悤�B
A�D�@��C���������S�����D(�}1��)�́A�O����͂��炭���͂�A���x�ɉ����āA�傫�����ς��B���̂ӂ�܂����A�ȉ��̂悤�ɒP�����������f���ōl���悤�B�}1�E�̂悤�ɒf�ʐ�S�̌Œ肳�ꂽ�V�����_�[���ɁA�Ȃ߂炩�ɓ����s�X�g��������B�V�����_�[�̒�ʂ̈ʒu�����_�Ƃ��āA�s�X�g���̈ʒu��x (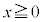 )�Ƃ���B�s�X�g���̓V�����_�[�̒�ʂƂ˂łȂ���Ă���B���̂˂͕��D�̃S����͂������z�I�Ȃ��̂ŁA���̑̐ς͖����ł���B�܂��A�˒萔��k (
)�Ƃ���B�s�X�g���̓V�����_�[�̒�ʂƂ˂łȂ���Ă���B���̂˂͕��D�̃S����͂������z�I�Ȃ��̂ŁA���̑̐ς͖����ł���B�܂��A�˒萔��k (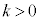 )�ł���A�s�X�g���́A���̂˂���傫��
)�ł���A�s�X�g���́A���̂˂���傫��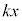 �̗͂�x���̕��̌����Ɏ�B�ȉ��A�s�X�g���ƃV�����_�[�Ƃ˂����킹�����̂��A���u�Ƃ�ԁB�V�����_�[�ɂ�n�����̒P���q���q���z�C�̂������Ă���A�V�����_�[�̊O���͐^��ł���B���̃s�X�g���ɑ��A�O��F����p������B�������A�O�͂͐}�̖��̌����𐳂Ƃ��A�����ǂ�������ɂ���������BF�����̏ꍇ�AF�͑�C���ɒu���ꂽ���D�ɑ�C���O����y�ڂ��͂�͂��Ă���B�܂��A�C�̂Ƒ��u����Ȃ�n�S�̂͏�Ɉ�l�ȉ��x�ł���A���̉��xT�͕ω������邱�Ƃ��ł���B�������A���u�̔M�e�ʂ͖����ł���B�ȉ��ł͂��ׂĂ̑�����\���ɂ������ƍs���B�܂��C�̒萔��R�Ƃ���B�ȉ��̖�ɓ�����B
�̗͂�x���̕��̌����Ɏ�B�ȉ��A�s�X�g���ƃV�����_�[�Ƃ˂����킹�����̂��A���u�Ƃ�ԁB�V�����_�[�ɂ�n�����̒P���q���q���z�C�̂������Ă���A�V�����_�[�̊O���͐^��ł���B���̃s�X�g���ɑ��A�O��F����p������B�������A�O�͂͐}�̖��̌����𐳂Ƃ��A�����ǂ�������ɂ���������BF�����̏ꍇ�AF�͑�C���ɒu���ꂽ���D�ɑ�C���O����y�ڂ��͂�͂��Ă���B�܂��A�C�̂Ƒ��u����Ȃ�n�S�̂͏�Ɉ�l�ȉ��x�ł���A���̉��xT�͕ω������邱�Ƃ��ł���B�������A���u�̔M�e�ʂ͖����ł���B�ȉ��ł͂��ׂĂ̑�����\���ɂ������ƍs���B�܂��C�̒萔��R�Ƃ���B�ȉ��̖�ɓ�����B
�T�D�܂��A�s�X�g�����Œ肵���ꍇ���l����B
��1�@���xT����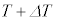 �ɔ����ɕω��������Ƃ��A�C�̂ɗ�������M��
�ɔ����ɕω��������Ƃ��A�C�̂ɗ�������M��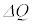 �����߂�B
�����߂�B
�U�D���ɁA�s�X�g�����Œ肹���Ɏ��R�ɓ�����悤�ɂ����ꍇ���l����B�������A�O�͍͂�p�������A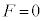 �Ƃ���B
�Ƃ���B
��2�@���xT�ɂ����ė͂��荇���A�s�X�g�����Î~�����ꍇ��x���Ak�Cn�CR�CT��p���ĕ\���B
��3�@���x��T����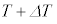 �ɔ����ω��������Ƃ��A�C�̂Ƃ˂���Ȃ�n�S�̂ɗ�������M��
�ɔ����ω��������Ƃ��A�C�̂Ƃ˂���Ȃ�n�S�̂ɗ�������M��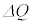 �����߂�B�܂��A���̌��ʂ�p���āA�n�S�̂̔M�e��C�����߂�B
�����߂�B�܂��A���̌��ʂ�p���āA�n�S�̂̔M�e��C�����߂�B
�V�D����ɁA�s�X�g�������R�ɓ�����悤�ɂ����܂܁A�O��F����p������ꍇ���l����B�K�v�Ȃ�A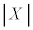 ��1���\���ɏ������Ƃ��Aa�𐳂̎����Ƃ���
��1���\���ɏ������Ƃ��Aa�𐳂̎����Ƃ���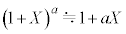 �CX��1���\���ɑ傫���Ƃ��A
�CX��1���\���ɑ傫���Ƃ��A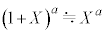 �Ƌߎ��ł��邱�Ƃ�p����B
�Ƌߎ��ł��邱�Ƃ�p����B
��4�@���xT�C�O��F�̉��Ńs�X�g�����Î~���Ă���ꍇ�́A�s�X�g���̈ʒux�����߂�B
��5�@��4�̌��ʂ�}�����悤�B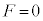 �ł�x��
�ł�x��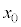 �Ƃ��A
�Ƃ��A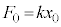 �Ƃ���B������p����
�Ƃ���B������p����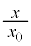 ��
��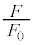 �����̊��Ƃ��ĕ\���B���ɁA������
�����̊��Ƃ��ĕ\���B���ɁA������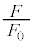 �C�c����
�C�c����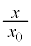 �Ƃ��āA���̊T�`���p���̃O���t�ɐ}������B
�Ƃ��āA���̊T�`���p���̃O���t�ɐ}������B ��6�@���xT�����ɕۂ����܂܁A�O�͂�F����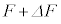 �܂Ŕ����ɕω��������Ƃ��A�s�X�g���̈ʒu��x����
�܂Ŕ����ɕω��������Ƃ��A�s�X�g���̈ʒu��x����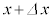 �܂Ŕ����ɕω������B���̂Ƃ��A
�܂Ŕ����ɕω������B���̂Ƃ��A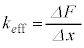 �͋C�̂Ƃ˂���Ȃ�n�́A�����I�Ȃ˒萔�Ƃ݂Ȃ���B�Ȃ��A
�͋C�̂Ƃ˂���Ȃ�n�́A�����I�Ȃ˒萔�Ƃ݂Ȃ���B�Ȃ��A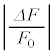 ��1�����\���ɏ������A
��1�����\���ɏ������A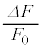 ��2���̍��͖������Ă悢�B
��2���̍��͖������Ă悢�B �ȉ��̏ꍇ�ɂ��āA��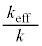 �����߂�B(a)
�����߂�B(a) 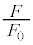 ������Ȃ��傫���ꍇ(b)
������Ȃ��傫���ꍇ(b) 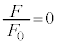 �̏ꍇ
�̏ꍇ
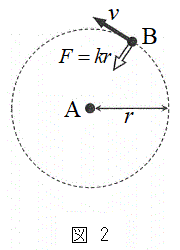 B�D�}2�̂悤�ɁA�d�C�I�ɒ����̗��qA�ƁA����Ɣ�r���ď\���Ɍy������M�̉דd���qB������A�����̊ԂɁA������͂��͂��炢�Ă��镨���n���l����B���̈��͂ɂ���āA�דd���qB�͒������qA�̎���ar�C����v�œ����~�^�����Ă���Ƃ���B���̈��͂̑傫��F�́A�݂��̋����ɔ�Ⴕ
B�D�}2�̂悤�ɁA�d�C�I�ɒ����̗��qA�ƁA����Ɣ�r���ď\���Ɍy������M�̉דd���qB������A�����̊ԂɁA������͂��͂��炢�Ă��镨���n���l����B���̈��͂ɂ���āA�דd���qB�͒������qA�̎���ar�C����v�œ����~�^�����Ă���Ƃ���B���̈��͂̑傫��F�́A�݂��̋����ɔ�Ⴕ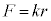 �@(
�@(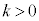 )
)�ŕ\�����B�������qA�͌��_�ɐÎ~���Ă���Ƃ��Ă悢�B�d�͂̌��ʂ͖�������B
��7�@�ȉ��̕��͂̋�(a)�`(h)�ɓ���ׂ����������ɋL������B
���̈��͂ɂ��דd���qB�̈ʒu�G�l���M�[U�́A���_����_�ɂƂ����Ƃ��A
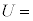 �@(a)�@
�@(a)�@�Ɨ^������B����A�דd���qB�̉�]�̒��S�����̉^�����������A
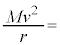 �@(b)�@
�@(b)�@�Ɨ^�����邱�Ƃ���A�דd���qB�̉^���G�l���M�[K�����܂�B����āA���̉דd���qB�̗͊w�I�G�l���M�[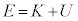 �́Ak��r��p����
�́Ak��r��p���� 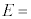 �@(c)�@
�@(c)�@�ƕ\�����Ƃ��ł���B
�h�E�u���C�ɂ��ƁA�~�N���Ȑ��E�ł́A���q�ɂ͔g�Ƃ��Ă̐���������A���̔g���͗��q�̉^���ʂ̑傫���̋t���ɔ�Ⴗ��B���l���Ă��镨���n�����q�Ɠ����x�ɏ������Ƃ���ƁA�דd���qB�ɂ��g�Ƃ��Ă̐���������Ă���B���̔g�̔g��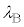 �́A�v�����N�萔��h�Ƃ����ƁAM�Ck�Ch�Cr��p����
�́A�v�����N�萔��h�Ƃ����ƁAM�Ck�Ch�Cr��p���� 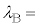 �@(d)�@
�@(d)�@�ŗ^������B
���āA�{�[�A�̐��f���q�̗��_�̏ꍇ�ɂȂ���āA���̕����n�ɗʎq�����ƐU�����������ۂ����Ƃ��l���悤�B
�܂��A���̗ʎq�������ۂ��B�u�דd���qB�̋O���̈���̒������A�g��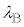 �̎��R���{(n�{)�ł���ꍇ�ɂ̂݁A�����(���g)����������v���̏ꍇ�ɁA�������O���̔��a�́An�ɑΉ������A�ƂтƂт̒l���Ƃ�B�����
�̎��R���{(n�{)�ł���ꍇ�ɂ̂݁A�����(���g)����������v���̏ꍇ�ɁA�������O���̔��a�́An�ɑΉ������A�ƂтƂт̒l���Ƃ�B�����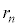 �Ƃ��āAM�Ck�Ch�Cn��p���ĕ\���ƁA
�Ƃ��āAM�Ck�Ch�Cn��p���ĕ\���ƁA 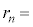 �@(e)�@�@(
�@(e)�@�@(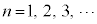 )
)�ƂȂ�B���ǁAn�Ԗڂ̋O�������דd���qB�̂��S�G�l���M�[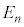 �́AM�Ck�Ch�Cn��p���āA
�́AM�Ck�Ch�Cn��p���āA 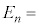 �@(f)�@�@(
�@(f)�@�@(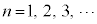 )
)�Ɨ^������B
����ɁA���̕����n�ɂ����āA���̐U�����������ۂ��Ƃ��悤�B�u�דd���qB��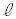 �Ԗڂ̒���Ԃ���A�G�l���M�[�����Ⴂn�Ԗڂ̒���ԂɈڂ鎞�ɁA���q1�����o�����v���̏ꍇ�ɁA
�Ԗڂ̒���Ԃ���A�G�l���M�[�����Ⴂn�Ԗڂ̒���ԂɈڂ鎞�ɁA���q1�����o�����v���̏ꍇ�ɁA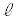 ��n��2�̒���Ԃ̊Ԃ̃G�l���M�[��
��n��2�̒���Ԃ̊Ԃ̃G�l���M�[��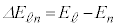 �́AM�Ck�Ch�Cn�C
�́AM�Ck�Ch�Cn�C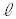 ��p���āA
��p���āA 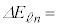 �@(g)�@�@(
�@(g)�@�@(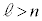 )
)�ƂȂ邩��A�^�ł̌��̑�����c�Ƃ���ƁA���o�������̔g��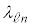 �́AM�Ck�Cn�C
�́AM�Ck�Cn�C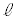 �Cc��p����
�Cc��p���� 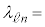 �@(h)�@�@(
�@(h)�@�@(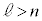 )
)�Ɨ^������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@ A�D�U�́A�˕t���s�X�g���̖��ł����A�舳�ω��ł���ϕω��ł������ω��ł��f�M�ω��ł��Ȃ����Ƃɒ��ӂ��K�v�ł��BpV�}�͒����ɂȂ�A4�̕ω��Ŏg���l�������g���܂���B
B�D�́A�˂̒e���͂̂悤�ȗ͂��ĉ~�^�����镨�̂ɗʎq�������ۂ��A�Ƃ������ł��B
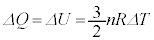 ......[��]
......[��]
�U�D��2�@�f�ʐ�S�C�C�̑��ݕ����̒���x���A�V�����_�[���̋C�̂̑̐ς�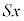 �C�C�̂̈��͂�P�Ƃ��āA�C�̂���ԕ������́A
�C�C�̂̈��͂�P�Ƃ��āA�C�̂���ԕ������́A 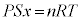 �@����@
�@����@�C�̂��s�X�g���������͂Ƃ˂̒e���͂Ƃ��荇�����A 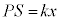 �@����A
�@����A����Ƈ@���A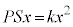 �C
�C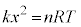 �@����B
�@����B �� 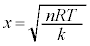 ......[��]
......[��]
��3�@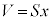 ���
���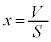 �ł��B������A�ɑ�����āA
�ł��B������A�ɑ�����āA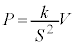 �CS�Ck�͒萔�Ȃ̂ŁA����P�͑̐�V�ɔ�Ⴕ�ApV�}�͒����ɂȂ�܂�(�����I�ω����Q��)�B���x��T����
�CS�Ck�͒萔�Ȃ̂ŁA����P�͑̐�V�ɔ�Ⴕ�ApV�}�͒����ɂȂ�܂�(�����I�ω����Q��)�B���x��T����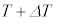 �ɕω����A�s�X�g���̈ʒu��x����
�ɕω����A�s�X�g���̈ʒu��x����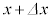 �ɕω�����Ƃ��ApV�}��V���Ƃ̊Ԃɋ��܂ꂽ�����̖ʐς��C�̂̂����d���ɂȂ�܂����A���̉ߒ��ł́A���̖ʐς͑�`�̖ʐςƂȂ�܂��B
�ɕω�����Ƃ��ApV�}��V���Ƃ̊Ԃɋ��܂ꂽ�����̖ʐς��C�̂̂����d���ɂȂ�܂����A���̉ߒ��ł́A���̖ʐς͑�`�̖ʐςƂȂ�܂��B ���x��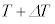 �̂Ƃ��̋C�̂̈��͂�
�̂Ƃ��̋C�̂̈��͂�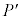 �Ƃ���ƁA���̂Ƃ��̃s�X�g���ɓ����͂̂荇���́A
�Ƃ���ƁA���̂Ƃ��̃s�X�g���ɓ����͂̂荇���́A 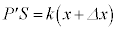 �@����C
�@����C���̉ߒ��ŋC�̂̂����d���́A��`�̖ʐςƂ��āA
�A�C�C��p���āA
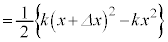 �@����D
�@����D���D�C�̂͂˂ɑ��Ďd��������̂ŁA�C�̂̂����d�����˂��e���G�l���M�[�̕ω��Ƃ��ċ��߂�A�ŏ����炱�̌`�ɂȂ�܂��B �B���A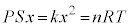 �@����E
�@����E
���x��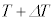 �̂Ƃ��̏�ԕ������́A
�̂Ƃ��̏�ԕ������́A 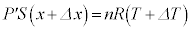 �@����F
�@����F�C�C�F���A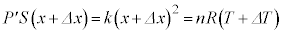 �@����G
�@����G
�G�|�E���A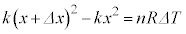
������A�D�ɑ�����āA �P���q���q���z�C�̂Ȃ̂ŁA���̉ߒ��ŁA�C�̂̓����G�l���M�[�̕ω��́A
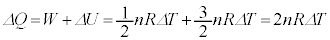 ......[��]
......[��]�n�S�̂̔M�e�ʂ�C�Ƃ��āA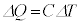 ���A
���A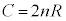 ......[��]
......[��]
�V�D��4�@�s�X�g���ɓ����͂̂荇�����A
�@�ɑ������ƁA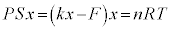
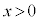 ���A
���A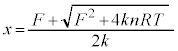 ......[��]
......[��]
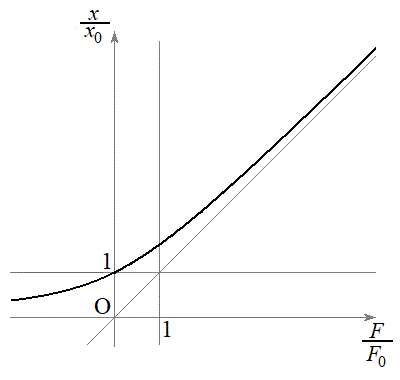 ��5�@��4�̌��ʂ�
��5�@��4�̌��ʂ�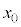 �Ŋ����āA
�Ŋ����āA��2�̌��ʂ��A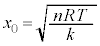 �C�����
�C�����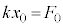 ���A
���A 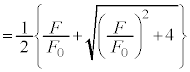 ......[��]�@����H
......[��]�@����H�O���t�͉E�}�B
��6�@�H��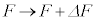 �C
�C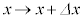 �Ƃ��āA
�Ƃ��āA 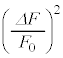 �����āA
�����āA��蕶���̋ߎ�����p���Ă���ɋߎ����s���A
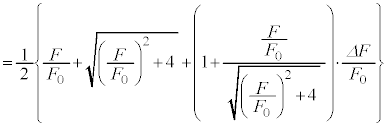 �@����I
�@����I�I�|�H���A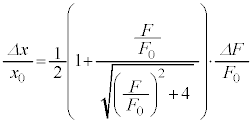
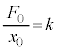 ���A
���A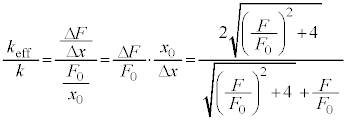 �@����J
�@����J(a) �J�ɂ����āA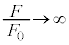 �Ƃ����(�s��`�̋Ɍ����Q��)�A
�Ƃ����(�s��`�̋Ɍ����Q��)�A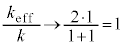 .......[��]
.......[��] (b) �J�ɂ����āA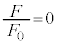 �Ƃ���ƁA
�Ƃ���ƁA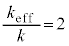 ......[��]
......[��]
B�D��7(a) �ʒu�G�l���M�[U�́A���͂ɋt�炤�O��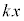 (x���傫���Ȃ����)�ɂ���_
(x���傫���Ȃ����)�ɂ���_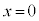 ����
����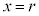 �܂ňړ�������̂ɕK�v���d���Ƃ��āA
�܂ňړ�������̂ɕK�v���d���Ƃ��āA 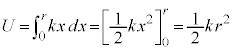 ......[��]
......[��]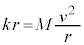 �@��
�@�� 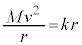 ......[��]
......[��]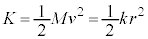 ��
�� 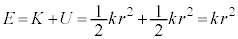 ......[��]
......[��](d) (b)�̌��ʂ��A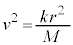 �@��
�@�� 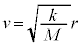
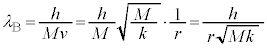 ......[��]
......[��](e) �ʎq�������A�~���̒�����g���̎��R��n�{�Ƃ��A�܂��A�דd���qB�ɋ������O�����a��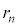 �Ƃ��āA
�Ƃ��āA (d)�̌��ʂ�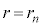 �Ƃ������̂�������ƁA
�Ƃ������̂�������ƁA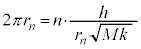
�� 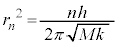
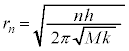 ......[��]
......[��] (f) ���a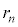 �̉~���O����̉דd���qB�̑S�G�l���M�[�́A(c)�C(e)�̌��ʂ��A
�̉~���O����̉דd���qB�̑S�G�l���M�[�́A(c)�C(e)�̌��ʂ��A 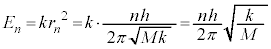 ......[��]
......[��](g) 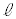 ��n��2�̒���Ԃ̊Ԃ̃G�l���M�[��
��n��2�̒���Ԃ̊Ԃ̃G�l���M�[��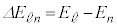 �́A(f)�̌��ʂ��A
�́A(f)�̌��ʂ��A 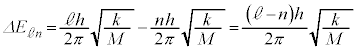 ......[��]
......[��](h) ���o�������̔g���́A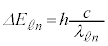 ���A
���A 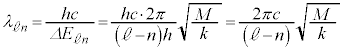 .......[��]
.......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 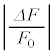 ��1�����\���ɏ������A
��1�����\���ɏ������A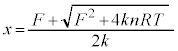 ......[��]
......[��]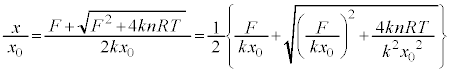
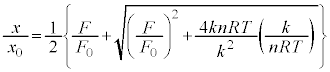
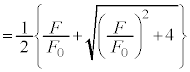 ......[��]�@����H
......[��]�@����H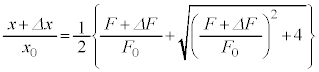
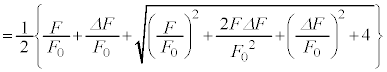
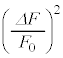 �����āA
�����āA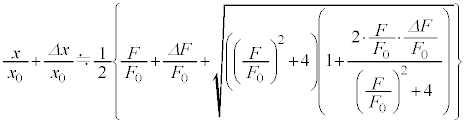
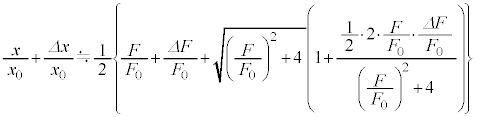
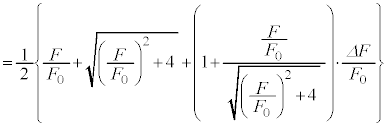 �@����I
�@����I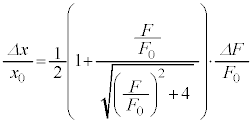
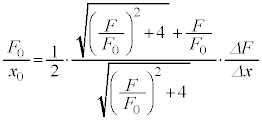
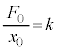 ���A
���A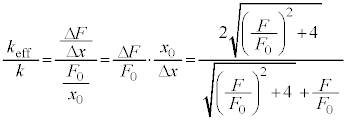 �@����J
�@����J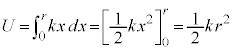 ......[��]
......[��]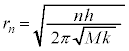 ......[��]
......[��]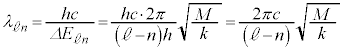 .......[��]
.......[��]