���嗝�H���w'08�N[1]
a�𐳂̒萔�Ƃ���Bxy-���W���ʂɂ����āA�Ȑ�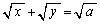 �ƁA����
�ƁA����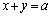 �Ƃň͂܂ꂽ������D�Ƃ����B�ȉ��̖�ɓ�����B
�Ƃň͂܂ꂽ������D�Ƃ����B�ȉ��̖�ɓ�����B
(1) D�̊T�`��`���A���̖ʐς����߂�B
(2) ����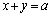 �����Ƃ��āAD��1��]���Ăł���}�`�̑̐ς����߂�B
�����Ƃ��āAD��1��]���Ăł���}�`�̑̐ς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�� �C�͂��K�v�Ȕ��ϕ��̌v�Z���ł����A(1)�́AD�̊T�`�𑨂���̂ɉ��ʂ܂ōl����K�v������̂ŁA�A���ň��������z���ɂ��Ă��܂��������Ղ��Ǝv���܂�(�A���̔����@���Q��)�B(2)�́A��^���ł����A��������̂͂Ȃ��Ȃ��e�Ղł͂���܂���B�����ł́A2�ʂ�̈����ł���Ă݂����Ǝv���܂��B�A���A�K�������A���W��]�Ń��N�ɂȂ�Ƃ������܂���(�Ɍ`�����Q��)�B
 (1) �Ȑ��F
(1) �Ȑ��F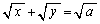 �@����@
�@����@�́A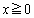 �C
�C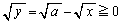 ���A
���A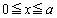 ���`��Ƃ��܂��B�܂��A�@�́A
���`��Ƃ��܂��B�܂��A�@�́A
�����F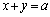 �@����A
�@����A
�Ƃ́A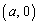 �C
�C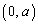 �����L���܂��B�@���A
�����L���܂��B�@���A ����āA�@��y�͒P�������ł�(���̑������Q��)�B 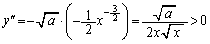 �@(
�@(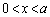 )
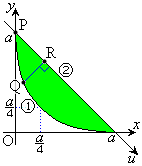
)����āA�@�̃O���t�͉��ɓʂł�(�Ƃ������Ƃ́A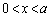 �ɂ����āA�@�̕����A�̉��ɗ���B���̉������Q��)�BD�̊T�`�́A�E�}�ʼn��ΐF�Œ��F���ꂽ�����B
�ɂ����āA�@�̕����A�̉��ɗ���B���̉������Q��)�BD�̊T�`�́A�E�}�ʼn��ΐF�Œ��F���ꂽ�����B
�A�́A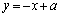 �ƕό`�ł���̂ŁAD�̖ʐ�S�́A
�ƕό`�ł���̂ŁAD�̖ʐ�S�́A 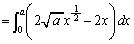
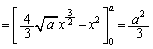 ......[��]
......[��]
(2) �E��}�ɂ����āA�Ȑ��@��̓_Q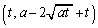 ���璼���A�ɉ��낵�������̑���R�C�_P
���璼���A�ɉ��낵�������̑���R�C�_P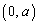 ���璼���A�ɉ����E���Ɍ�������u�����Ƃ�A
���璼���A�ɉ����E���Ɍ�������u�����Ƃ�A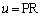 �Ƃ��܂��B
�Ƃ��܂��B ���̂Ƃ��A�_R�̑��ݔ͈́F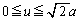 ���l���āAD���A�����Ƃ��ĉ�]�����Ăł���}�`�̑̐�V�́A
���l���āAD���A�����Ƃ��ĉ�]�����Ăł���}�`�̑̐�V�́A �ƕ\����܂��B�_Q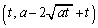 �ƒ����F
�ƒ����F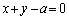 �Ƃ̋������l���邱�Ƃɂ��A
�Ƃ̋������l���邱�Ƃɂ��A 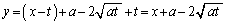 �@����E
�@����E�A�ƇE��A�����邱�Ƃɂ��A��_R��x���W�́A
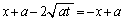 ��
�� 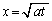
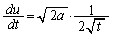 ��
�� 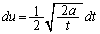
u�F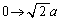 �̂Ƃ��At�F
�̂Ƃ��At�F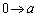
����āA�C�́A�F�̒u���ɂ��(�u���ϕ����Q��)�A�D��p���āA (u�̐ϕ��̂܂܂ł��ł��܂����A��[��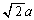 �ƂȂ���
�ƂȂ���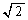 ������������ʓ|�ł�)
������������ʓ|�ł�)
�ʉ� �ʐςƉ�]�̂̑̐ς����W��]�ł���Ă݂܂�(�Ɍ`�����Q��)�B
���f��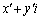 �����v���(������)��
�����v���(������)��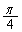 ��]���āA
��]���āA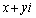 �ɂȂ�Ƃ���ƁA
�ɂȂ�Ƃ���ƁA
�� 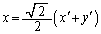 �C
�C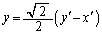 �@����G
�@����G �B�ɑ������ƁA
2�悷��ƁA
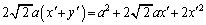 ��
�� 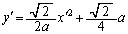
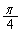 ��]����ƁA�������F
��]����ƁA�������F
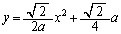 �@����H
�@����H
�G���A�ɑ������ƁA
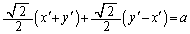 ��
�� 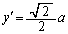
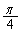 ��]����ƁA�����F
��]����ƁA�����F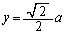 �ƂȂ�܂��B
�ƂȂ�܂��B
�H�ƘA������ƁA
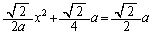 ��
�� 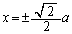
(2)�̑̐�V�́A
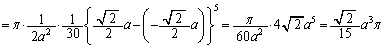 ......[��]
......[��]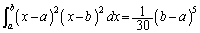 �ł��B
�ł��B
�Ȑ��ƒ����̎���ϊ�����K�v������܂����A�ϕ��v�Z�̓��N�ɂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B