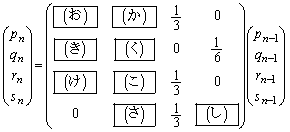ڈêچ‡‚جگ”پEٹm—¦پE“ٌچ€’è—‰‰ڈK–â‘è
‹م‘ه—Œnگ”ٹw'09”NŒمٹْ[4]
پyچLچگپz‚±‚±‚©‚çچLچگ‚إ‚·پB‚²——‚جٹF‚³‚ـ‚ج‚²ژx‰‡‚²—‰ً‚ًژ’‚肽‚پA‚و‚낵‚‚¨ٹè‚¢‚¢‚½‚µ‚ـ‚·پB
پyچLچگپzچLچگ‚ح‚±‚±‚ـ‚إ‚إ‚·پB
“_Q‚حژں‚ج‹K‘¥‚إگ”’¼گüڈم‚ج•‰‚إ‚ب‚¢گ®گ”‚جڈم‚ًگ³‚ج•ûŒü‚ض“®‚‚à‚ج‚ئ‚·‚éپB‚½‚¾‚µn‚ح•‰‚إ‚ب‚¢گ®گ”‚ئ‚·‚éپB
(a) ژچڈ0‚إ‚ح“_Q‚حŒ´“_‚ة‚ ‚éپB
(b) “_Q‚ھژچڈT‚إچہ•W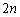 ‚ة‚ ‚é‚ئ‚«پAژچڈ
‚ة‚ ‚é‚ئ‚«پAژچڈ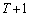 ‚ة‚حٹm—¦
‚ة‚حٹm—¦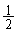 ‚إچہ•W
‚إچہ•W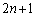 ‚ضˆع“®‚µپAٹm—¦
‚ضˆع“®‚µپAٹm—¦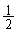 ‚إچہ•W
‚إچہ•W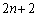 ‚ضˆع“®‚·‚éپB
‚ضˆع“®‚·‚éپB (c) “_Q‚ھژچڈT‚إچہ•W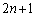 ‚ة‚ ‚é‚ئ‚«پAژچڈ
‚ة‚ ‚é‚ئ‚«پAژچڈ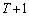 ‚ة‚حٹm—¦1‚إچہ•W
‚ة‚حٹm—¦1‚إچہ•W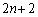 ‚ضˆع“®‚·‚éپB
‚ضˆع“®‚·‚éپB “_Q‚ھژچڈT‚إچہ•Wj‚ة‚ ‚éٹm—¦‚ً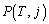 ‚ئڈ‘‚‚±‚ئ‚ة‚·‚éپBˆب‰؛‚ج–â‚¢‚ة“ڑ‚¦‚وپB
‚ئڈ‘‚‚±‚ئ‚ة‚·‚éپBˆب‰؛‚ج–â‚¢‚ة“ڑ‚¦‚وپB
(1) ‚·‚ׂؤ‚جژ©‘Rگ”j‚ة‘خ‚µ‚ؤ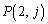 ‚ً‹پ‚ك‚وپB
‚ً‹پ‚ك‚وپB (2) TپCj‚ھژ©‘Rگ”‚إ‚ ‚é‚ئ‚«پA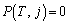 ‚ئ‚ب‚éڈًŒڈ‚ًTپCj‚ً—p‚¢‚ؤ•\‚¹پB
‚ئ‚ب‚éڈًŒڈ‚ًTپCj‚ً—p‚¢‚ؤ•\‚¹پB (3) T‚ھژ©‘Rگ”‚إ‚ ‚é‚ئ‚«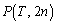 ‚ً‹پ‚ك‚وپB
‚ً‹پ‚ك‚وپB [‰ً“ڑ‚ض]
‘هچم‹³ˆç‘هگ”ٹw'09”N[4]
1Œآ‚ج‚³‚¢‚±‚ë‚ًn‰ٌ“ٹ‚°‚é‚ئ‚«پAk‰ٌ–ع‚ةڈo‚½–ع‚ً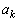 ‚ئ‚µپA‚»‚ê‚ç‚جگد
‚ئ‚µپA‚»‚ê‚ç‚جگد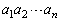 ‚ً
‚ً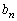 ‚ئ‚·‚éپB‚»‚µ‚ؤ
‚ئ‚·‚éپB‚»‚µ‚ؤ ‚ھrŒ…‚جژ©‘Rگ”‚ئ‚ب‚éٹm—¦‚ً
‚ھrŒ…‚جژ©‘Rگ”‚ئ‚ب‚éٹm—¦‚ً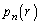 ‚ئ‚·‚éپBژں‚ج–â‚¢‚ة“ڑ‚¦‚وپB
‚ئ‚·‚éپBژں‚ج–â‚¢‚ة“ڑ‚¦‚وپB
(1) 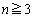 ‚ج‚ئ‚«پA
‚ج‚ئ‚«پA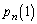 ‚ًn‚ً—p‚¢‚ؤ•\‚¹پB
‚ًn‚ً—p‚¢‚ؤ•\‚¹پB (2)(i) 1Œآ‚ج‚³‚¢‚±‚ë‚ًn‰ٌ“ٹ‚°‚é‚ئ‚«پA1ˆبٹO‚ج–ع‚ھ‚؟‚ه‚¤‚اs‰ٌڈo‚éٹm—¦‚ً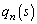 ‚ئ‚·‚éپB
‚ئ‚·‚éپB ‚ًs‚ً—p‚¢‚ؤ•\‚¹پB
‚ًs‚ً—p‚¢‚ؤ•\‚¹پB (ii)  ‚ً‹پ‚ك‚وپB
‚ً‹پ‚ك‚وپB [‰ً“ڑ‚ض]
‹مڈBچH‘هڈî•ٌگ”ٹw'09”N[4]
” ‚ج’†‚ةپAگ”ژڑ‚ج1‚ً‹L“ü‚µ‚½ƒJپ[ƒhپA2‚ً‹L“ü‚µ‚½ƒJپ[ƒhپA3‚ً‹L“ü‚µ‚½ƒJپ[ƒh‚ھ‚»‚ꂼ‚ên–‡پAچ‡Œv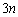 –‡“ü‚ء‚ؤ‚¢‚éپB‚½‚¾‚µپA
–‡“ü‚ء‚ؤ‚¢‚éپB‚½‚¾‚µپA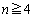 ‚إ‚ ‚èپA‚ـ‚½ƒJپ[ƒh‚ج— ‘¤‚ة‚ح‰½‚àڈ‘‚©‚ê‚ؤ‚¢‚ب‚¢‚à‚ج‚ئ‚·‚éپBˆب‰؛‚ج–â‚¢‚ة“ڑ‚¦‚وپB
‚إ‚ ‚èپA‚ـ‚½ƒJپ[ƒh‚ج— ‘¤‚ة‚ح‰½‚àڈ‘‚©‚ê‚ؤ‚¢‚ب‚¢‚à‚ج‚ئ‚·‚éپBˆب‰؛‚ج–â‚¢‚ة“ڑ‚¦‚وپB
(1) ” ‚ج’†‚©‚çƒJپ[ƒh‚ً1–‡ژو‚èڈo‚µپAگ”ژڑ‚ًŒ©‚ب‚¢‚إ•ڑ‚¹‚ؤ‚¨‚پBژں‚ة” ‚ج’†‚©‚çژو‚èڈo‚µ‚½ƒJپ[ƒh‚جگ”ژڑ‚ھ1‚إ‚ ‚éٹm—¦‚ً‹پ‚ك‚وپB
(2) ” ‚ج’†‚©‚ç2–‡‚جƒJپ[ƒh‚ً“¯ژ‚ةژو‚èڈo‚µ‚½‚ئ‚«پAƒJپ[ƒh‚جگ”ژڑ‚ھˆظ‚ب‚éٹm—¦‚ًn‚ً—p‚¢‚ؤ•\‚¹پB
(3) ” ‚ج’†‚©‚ç3–‡‚جƒJپ[ƒh‚ً“¯ژ‚ةژو‚èڈo‚µ‚½‚ئ‚«پAƒJپ[ƒh‚جگ”ژڑ‚ھ‚؟‚ه‚¤‚ا2ژي—ق‚إ‚ ‚éٹm—¦‚ًn‚ً—p‚¢‚ؤ•\‚¹پB
(4) ” ‚ج’†‚©‚ç4–‡‚جƒJپ[ƒh‚ً“¯ژ‚ةژو‚èڈo‚µ‚½‚ئ‚«پAƒJپ[ƒh‚جگ”ژڑ‚ھ‚؟‚ه‚¤‚ا2ژي—ق‚إ‚ ‚éٹm—¦‚ًn‚ً—p‚¢‚ؤ•\‚¹پB
[‰ً“ڑ‚ض]
ٹٍ•Œ–ٍ‰ب‘هگ”ٹw'09”N[5]
چ½ڈَچ‚•ھژq‚حپA’P—ت‘ج‚ئŒؤ‚خ‚ê‚é’Pˆت‚جŒJ‚è•ش‚µ‚©‚çگ¬‚ء‚ؤ‚¢‚ؤپA‚آ‚ب‚ھ‚ء‚½’P—ت‘ج‚ھˆت’u‚ً•د‚¦‚邱‚ئ‚ة‚و‚èپAژيپX‚جŒ`‚ً‚ئ‚éپBNŒآ‚ج’P—ت‘ج‚©‚ç‚ب‚éچ½ڈَچ‚•ھژq‚جŒ`‚ًپAژں‚جگ”ٹwƒ‚ƒfƒ‹‚إچlژ@‚µ‚½پB
‡@پ@چ½ڈَچ‚•ھژq‚جNŒآ‚ج’P—ت‘ج‚ح•½–تڈم‚جˆت’u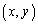 (xپCy‚حگ®گ”)‚ً‚ئ‚èپAŒ‹چ‡‚µ‚ؤ‚¢‚é’P—ت‘جٹش‚ج‹——£‚ھ1‚إ‚ ‚éپB
(xپCy‚حگ®گ”)‚ً‚ئ‚èپAŒ‹چ‡‚µ‚ؤ‚¢‚é’P—ت‘جٹش‚ج‹——£‚ھ1‚إ‚ ‚éپB ‡Aپ@1”ش–ع‚ج’P—ت‘ج‚حپAˆت’u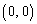 ‚ة‚ ‚éپB
‚ة‚ ‚éپB ‡Bپ@کA‘±‚µ‚ؤ‚آ‚ب‚ھ‚é3Œآ‚ج’P—ت‘ج‚حپA’¼گüپA‰E‰ٌ‚è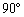 پCچ¶‰ٌ‚è
پCچ¶‰ٌ‚è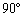 ‚ج‚¢‚¸‚ê‚©‚جˆت’u‚ة‚ ‚éپB—ل‚¦‚خپA2”ش–ع‚ج’P—ت‘ج‚ھˆت’u
‚ج‚¢‚¸‚ê‚©‚جˆت’u‚ة‚ ‚éپB—ل‚¦‚خپA2”ش–ع‚ج’P—ت‘ج‚ھˆت’u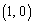 ‚ة‚ ‚é‚ئ‚«پA3”ش–ع‚ج’P—ت‘ج‚حپA
‚ة‚ ‚é‚ئ‚«پA3”ش–ع‚ج’P—ت‘ج‚حپA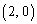 پC
پC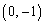 پC
پC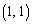 ‚ج‚¢‚¸‚ê‚©‚جˆت’u‚ة‚ ‚éپB
‚ج‚¢‚¸‚ê‚©‚جˆت’u‚ة‚ ‚éپB ‡Cپ@‚¢‚¸‚ê‚ج’P—ت‘ج‚à‘¼‚ج’P—ت‘ج‚ئ“¯‚¶ˆت’u‚ة‚ ‚邱‚ئ‚ح‚ب‚¢پB
‚ب‚¨پANŒآ‚ج’P—ت‘ج‚ً‚à‚آ2‚آ‚جچ½ڈَچ‚•ھژq‚ة‚¨‚¢‚ؤپAٹe’P—ت‘ج‚ھ“¯‚¶ˆت’u‚ئڈ‡ڈک‚إڈd‚ب‚éڈêچ‡‚ة“¯‚¶Œ`‚ئ‚ف‚ب‚·پBژں‚ج–â‚¢‚ة“ڑ‚¦‚وپB
(1) 10Œآ‚ج’P—ت‘ج‚©‚ç‚ب‚éچ½ڈَچ‚•ھژq‚إپA10”ش–ع‚ج’P—ت‘ج‚ھˆت’u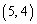 ‚ة‚ ‚é‚ئ‚«پA‚±‚جچ½ڈَچ‚•ھژq‚حپA‰½’ت‚è‚جŒ`‚ً‚ئ‚肦‚é‚©پB10”ش–ع‚ج’P—ت‘ج‚ھˆت’u
‚ة‚ ‚é‚ئ‚«پA‚±‚جچ½ڈَچ‚•ھژq‚حپA‰½’ت‚è‚جŒ`‚ً‚ئ‚肦‚é‚©پB10”ش–ع‚ج’P—ت‘ج‚ھˆت’u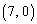 ‚ة‚ ‚é‚ئ‚«پA‰½’ت‚è‚جŒ`‚ً‚ئ‚肦‚é‚©پB10”ش–ع‚ج’P—ت‘ج‚ھˆت’u
‚ة‚ ‚é‚ئ‚«پA‰½’ت‚è‚جŒ`‚ً‚ئ‚肦‚é‚©پB10”ش–ع‚ج’P—ت‘ج‚ھˆت’u ‚ة‚ ‚é‚ئ‚«پA‰½’ت‚è‚جŒ`‚ً‚ئ‚肦‚é‚©پB
‚ة‚ ‚é‚ئ‚«پA‰½’ت‚è‚جŒ`‚ً‚ئ‚肦‚é‚©پB (2) 2”ش–ع‚ج’P—ت‘ج‚ھˆت’u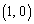 ‚ة‚ ‚é5Œآ‚ج’P—ت‘ج‚©‚ç‚ب‚éچ½ڈَچ‚•ھژq‚ًچl‚¦‚éپBچ½ڈَچ‚•ھژq‚ج‰آ”\‚بŒ`‚حپA‚·‚ׂؤ“™‚µ‚¢•p“x‚إŒ»‚ê‚é‚à‚ج‚ئ‚·‚éپB1”ش–ع‚ج’P—ت‘ج‚ئ5”ش–ع‚ج’P—ت‘ج‚ج‹——£‚ًd‚ئ‚·‚é‚ئ‚«پA
‚ة‚ ‚é5Œآ‚ج’P—ت‘ج‚©‚ç‚ب‚éچ½ڈَچ‚•ھژq‚ًچl‚¦‚éپBچ½ڈَچ‚•ھژq‚ج‰آ”\‚بŒ`‚حپA‚·‚ׂؤ“™‚µ‚¢•p“x‚إŒ»‚ê‚é‚à‚ج‚ئ‚·‚éپB1”ش–ع‚ج’P—ت‘ج‚ئ5”ش–ع‚ج’P—ت‘ج‚ج‹——£‚ًd‚ئ‚·‚é‚ئ‚«پA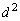 ‚ھ2‚ئ‚ب‚éٹm—¦‚ً‹پ‚ك‚وپB‚ـ‚½پA
‚ھ2‚ئ‚ب‚éٹm—¦‚ً‹پ‚ك‚وپB‚ـ‚½پA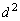 ‚ج•½‹د’l(ٹْ‘ز’l)‚ً‹پ‚ك‚وپB
‚ج•½‹د’l(ٹْ‘ز’l)‚ً‹پ‚ك‚وپB [‰ً“ڑ‚ض]
–¼‘ه—Œnگ”ٹw'08”N[4B]
‘ـA‚ج’†‚ةگش‹ت‚ئ”’‹ت‚ھ‚»‚ꂼ‚ê4‚آ“ü‚ء‚ؤ‚¢‚邱‚ئ‚ئپA‘ـB‚ج’†‚ةگش‹ت3‚آ‚ئ”’‹ت2‚آ‚ھ“ü‚ء‚ؤ‚¢‚邱‚ئ‚ھ•ھ‚©‚ء‚ؤ‚¢‚éپB
(1) ‘ـB‚©‚ç2‚آ‚ج‹ت‚ًژو‚èڈo‚·‚ئ‚«پAژو‚èڈo‚³‚ê‚éگش‹ت‚جŒآگ”‚جٹْ‘ز’l‚ً‹پ‚ك‚وپB
(2) ‘ـA‚©‚ç3‚آ‚ج‹ت‚ًژو‚èڈo‚µپA‚»‚ج‚ ‚ئ‘ـB‚©‚ç2‚آ‚ج‹ت‚ًژو‚èڈo‚·پB‚»‚ج5‚آ‚ج‹ت‚ج‚¤‚؟گش‹ت‚ھ3‚آ‚إ‚ ‚éٹm—¦‚ً‹پ‚ك‚وپB
(3) ‘ـA‚©‚ç3‚آ‚ج‹ت‚ًژو‚èڈo‚µ‚½‚ ‚ئ‚إپA2‚آ‚ج‹ت‚ً‘ـA‚©‚çژو‚èڈo‚·‚©‚ ‚é‚¢‚ح2‚آ‚ج‹ت‚ً‘ـB‚©‚çژو‚èڈo‚·‚©‚ج‚ا‚؟‚ç‚©‚ً‘I‘ً‚إ‚«‚é‚ئ‚·‚éپB‚إ‚«‚邾‚¯‘½‚‚جگش‹ت‚ًژو‚èڈo‚»‚¤‚ئ‘I‘ً‚µ‚½‚ئ‚«پAچإڈI“I‚ةژو‚èڈo‚³‚ê‚éگش‹ت‚جŒآگ”‚جٹْ‘ز’l‚ً‹پ‚ك‚وپB
[‰ً“ڑ‚ض]
“Œ–k‘ه—Œnگ”ٹw'09”NŒمٹْ[2]
ƒAƒپ‹ت‚ج“ü‚ء‚½ٹت‚ھ‚ ‚éپB”’‚جƒAƒپ‹ت‚ھ11ŒآپAگش‰©—خگآ‚ج4گF‚جƒAƒپ‹ت‚ھ‚»‚ꂼ‚ê1Œآ‚¸‚آپAچ‡Œv15Œآ“ü‚ء‚ؤ‚¢‚éپBٹت‚ج’†گg‚ً‚و‚چ¬‚؛‚ؤ‚©‚ç3Œآ“¯ژ‚ةژو‚èڈo‚·پBژو‚èڈo‚µ‚½3Œآ‚ة‚آ‚¢‚ؤˆب‰؛‚جٹm—¦‚ئٹْ‘ز’l‚ً‹پ‚ك‚وپB
(1) 3Œآ‚ئ‚à”’‚جƒAƒپ‹ت‚إ‚ ‚éٹm—¦پB
(2) —خ‚جƒAƒپ‹ت‚ھٹـ‚ـ‚ê‚éٹm—¦پB
(3) —خ‚ئگآ‚جƒAƒپ‹ت‚جŒآگ”‚جچ‡Œv‚جٹْ‘ز’lپB
(4) ”’ˆبٹO‚جƒAƒپ‹ت‚جŒآگ”‚جٹْ‘ز’lپB
[‰ً“ڑ‚ض]
‹‘ه—Œnگ”ٹw'96”N‘Oٹْ[5]
xy•½–تڈم‚جگ³ژOٹpŒ`پ¢ABC‚ًچl‚¦‚éپBپ¢ABC‚جڈdگS‚حŒ´“_O‚ة‚ ‚èپAƒxƒNƒgƒ‹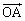 ‚ج’·‚³‚ح1‚ئ‚·‚éپBپ¢ABC‚ج“à•”‚ـ‚½‚ح•سڈم‚ج“_
‚ج’·‚³‚ح1‚ئ‚·‚éپBپ¢ABC‚ج“à•”‚ـ‚½‚ح•سڈم‚ج“_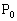 ‚ة‘خ‚µپA3’¸“_AپCBپCC‚©‚ç1“_‚ً“™ٹm—¦
‚ة‘خ‚µپA3’¸“_AپCBپCC‚©‚ç1“_‚ً“™ٹm—¦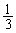 ‚إ‘I‚رپA‚±‚ج’¸“_‚ئ
‚إ‘I‚رپA‚±‚ج’¸“_‚ئ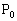 ‚ج’†“_‚ً
‚ج’†“_‚ً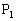 ‚ئ‚·‚éپBژں‚ة“_
‚ئ‚·‚éپBژں‚ة“_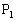 ‚ة‘خ‚µ‚ؤ“¯—l‚ج‘€چى‚ًچs‚¢“¾‚ç‚ꂽ“_‚ً
‚ة‘خ‚µ‚ؤ“¯—l‚ج‘€چى‚ًچs‚¢“¾‚ç‚ꂽ“_‚ً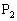 ‚ئ‚µپAˆب‰؛‚±‚ج‘€چى‚ًŒJ‚è•ش‚µ‚ؤپA“_
‚ئ‚µپAˆب‰؛‚±‚ج‘€چى‚ًŒJ‚è•ش‚µ‚ؤپA“_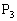 پC
پC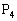 پC¥¥¥پC
پC¥¥¥پC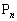 ‚ًچى‚éپBƒxƒNƒgƒ‹
‚ًچى‚éپBƒxƒNƒgƒ‹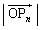 ‚ج’·‚³‚ج2ڈو
‚ج’·‚³‚ج2ڈو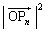 ‚جٹْ‘ز’l‚ً
‚جٹْ‘ز’l‚ً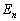 ‚ئ‚¨‚پB
‚ئ‚¨‚پB
(1) 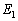 ‚ًƒxƒNƒgƒ‹
‚ًƒxƒNƒgƒ‹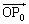 ‚ج’·‚³‚ً—p‚¢‚ؤ•\‚¹پB
‚ج’·‚³‚ً—p‚¢‚ؤ•\‚¹پB (2) ‘I‚ٌ‚¾’¸“_‚ھ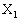 پC
پC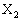 پC¥¥¥پC
پC¥¥¥پC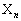 ‚ج‚ئ‚«پAƒxƒNƒgƒ‹
‚ج‚ئ‚«پAƒxƒNƒgƒ‹ ‚ًƒxƒNƒgƒ‹
‚ًƒxƒNƒgƒ‹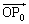 ‚ئ
‚ئ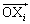 پC
پC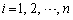 ‚ً—p‚¢‚ؤ•\‚¹پB
‚ً—p‚¢‚ؤ•\‚¹پB (3) 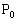 ‚ھŒ´“_O‚ج‚ئ‚«
‚ھŒ´“_O‚ج‚ئ‚«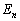 ‚ً‹پ‚ك‚وپB
‚ً‹پ‚ك‚وپB [‰ً“ڑ‚ض]
‹مڈBچH‘هڈî•ٌگ”ٹw'08”N‘Oٹْ[4]
ڈoگبژزnگl‚ج‰ï‹c‚إپAڈoگبژز‚ج‚¤‚؟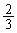 ˆبڈم‚ھ‹cˆؤ‚ةژ^گ¬‚·‚éٹm—¦
ˆبڈم‚ھ‹cˆؤ‚ةژ^گ¬‚·‚éٹm—¦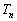 ‚ئپA
‚ئپA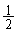 ˆبڈم‚ھژ^گ¬‚·‚éٹm—¦
ˆبڈم‚ھژ^گ¬‚·‚éٹm—¦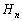 ‚ًچl‚¦‚éپBٹeڈoگبژز‚ھ‹cˆؤ‚ةژ^گ¬‚·‚éٹm—¦‚ًp (
‚ًچl‚¦‚éپBٹeڈoگبژز‚ھ‹cˆؤ‚ةژ^گ¬‚·‚éٹm—¦‚ًp (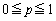 )‚ئ‚µپAٹeڈoگبژز‚ھژ^گ¬‚·‚é‚©‚µ‚ب‚¢‚©‚حŒف‚¢‚ة“ئ—§‚إ‚ ‚é‚ئ‚·‚éپB
)‚ئ‚µپAٹeڈoگبژز‚ھژ^گ¬‚·‚é‚©‚µ‚ب‚¢‚©‚حŒف‚¢‚ة“ئ—§‚إ‚ ‚é‚ئ‚·‚éپB
‚½‚ئ‚¦‚خپA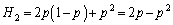 ‚إ‚ ‚éپB
‚إ‚ ‚éپB
(1) 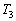 ‚ً‹پ‚ك‚وپB
‚ً‹پ‚ك‚وپB (2) 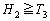 ‚ًژ¦‚¹پB
‚ًژ¦‚¹پB (3) چ·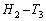 ‚ھچإ‚à‘ه‚«‚‚ب‚é‚ئ‚«‚جp‚ج’l‚ً‹پ‚ك‚وپB
‚ھچإ‚à‘ه‚«‚‚ب‚é‚ئ‚«‚جp‚ج’l‚ً‹پ‚ك‚وپB (4) 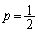 ‚ج‚ئ‚«پA
‚ج‚ئ‚«پA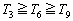 ‚ًژ¦‚¹پB
‚ًژ¦‚¹پB (5) 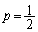 ‚ج‚ئ‚«پA
‚ج‚ئ‚«پA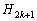 (
(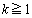 )‚ً‹پ‚ك‚وپB
)‚ً‹پ‚ك‚وپB [‰ً“ڑ‚ض]
‹م‘ه—Œnگ”ٹw'09”N‘Oٹْ[2]
k‚ح2ˆبڈم‚جژ©‘Rگ”‚ئ‚·‚éپBپu1پv‚ئڈ‘‚©‚ꂽƒJپ[ƒh‚ھ1–‡پAپu2پv‚ئڈ‘‚©‚ꂽƒJپ[ƒh‚ھ2–‡پA¥¥¥پAپukپv‚ئڈ‘‚©‚ꂽƒJپ[ƒh‚ھk–‡‚ ‚éپB‚»‚ج‚¤‚؟‚ج‹ôگ”‚ھڈ‘‚©‚ꂽƒJپ[ƒh‚ج–‡گ”‚ًMپCٹïگ”‚ھڈ‘‚©‚ꂽƒJپ[ƒh‚ج–‡گ”‚ًN‚إ•\‚·پB‚±‚ج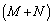 –‡‚جƒJپ[ƒh‚ً‚و‚‚«‚ء‚ؤ1–‡‚ًژو‚èڈo‚µپA‚»‚±‚ةڈ‘‚©‚ꂽگ”‚ً‹Lک^‚µ‚ؤ‚à‚ئ‚ة–ك‚·‚ئ‚¢‚¤‘€چى‚ًn‰ٌŒJ‚è•ش‚·پB‹Lک^‚³‚ꂽnŒآ‚جگ”‚جکa‚ھ‹ôگ”‚ئ‚ب‚éٹm—¦‚ً
–‡‚جƒJپ[ƒh‚ً‚و‚‚«‚ء‚ؤ1–‡‚ًژو‚èڈo‚µپA‚»‚±‚ةڈ‘‚©‚ꂽگ”‚ً‹Lک^‚µ‚ؤ‚à‚ئ‚ة–ك‚·‚ئ‚¢‚¤‘€چى‚ًn‰ٌŒJ‚è•ش‚·پB‹Lک^‚³‚ꂽnŒآ‚جگ”‚جکa‚ھ‹ôگ”‚ئ‚ب‚éٹm—¦‚ً ‚ئ‚·‚éپBژں‚ج–â‚¢‚ة“ڑ‚¦‚وپB
‚ئ‚·‚éپBژں‚ج–â‚¢‚ة“ڑ‚¦‚وپB
(1) 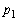 ‚ئ
‚ئ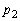 ‚ًMپCN‚إ•\‚¹پB
‚ًMپCN‚إ•\‚¹پB (2) 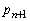 ‚ً
‚ً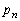 پCMپCN‚إ•\‚¹پB
پCMپCN‚إ•\‚¹پB (3) 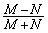 ‚ًk‚إ•\‚¹پB
‚ًk‚إ•\‚¹پB (4)  ‚ًn‚ئk‚إ•\‚¹پB
‚ًn‚ئk‚إ•\‚¹پB [‰ً“ڑ‚ض]
Œc‘هˆمگ”ٹw'09”N[3]
ˆب‰؛‚ج•¶ڈح‚ج‹َ—“‚ة“Kگط‚بگ”‚ـ‚½‚حژ®‚ً“ü‚ê‚ؤ•¶ڈح‚ًٹ®گ¬‚³‚¹‚ب‚³‚¢پB‚ـ‚½پAگف–â(3)‚ة“ڑ‚¦‚ب‚³‚¢پB
گ³•ûŒ`‚ج4‚آ‚ج’¸“_‚ة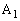 پC
پC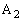 پC
پC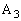 پC
پC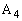 ‚جڈ‡‚ة”½ژŒv‰ٌ‚è‚ة–¼‘O‚ً‚آ‚¯‚éپB
‚جڈ‡‚ة”½ژŒv‰ٌ‚è‚ة–¼‘O‚ً‚آ‚¯‚éپB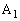 پC
پC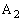 ڈم‚ة‚ح•\‚ًڈم‚ة‚µ‚½چd‰ف‚ً1–‡‚¸‚آ’u‚«پA
ڈم‚ة‚ح•\‚ًڈم‚ة‚µ‚½چd‰ف‚ً1–‡‚¸‚آ’u‚«پA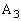 پC
پC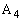 ڈم‚ة‚ح— ‚ًڈم‚ة‚µ‚½چd‰ف‚ً1–‡‚¸‚آ’u‚پB‚¢‚ـژں‚ج‘€چىT‚ً‰½‰ٌ‚©ŒJ‚è•ش‚µچs‚¤پB
ڈم‚ة‚ح— ‚ًڈم‚ة‚µ‚½چd‰ف‚ً1–‡‚¸‚آ’u‚پB‚¢‚ـژں‚ج‘€چىT‚ً‰½‰ٌ‚©ŒJ‚è•ش‚µچs‚¤پB
‘€چىTپF4‚آ‚ج’¸“_‚ج‚ا‚ê‚©‚ًٹm—¦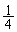 ‚¸‚آ‚إ‘I‚شپB‘I‚خ‚ꂽ’¸“_‚ً ‚¸‚آ‚إ‘I‚شپB‘I‚خ‚ꂽ’¸“_‚ً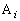
(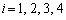 )‚ئ‚·‚é‚ئ‚«پA•س‚ة‰ˆ‚ء‚ؤ )‚ئ‚·‚é‚ئ‚«پA•س‚ة‰ˆ‚ء‚ؤ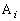 ڈم‚جچd‰ف‚ئ•ہ‚ٌ‚إ‚¢‚é ڈم‚جچd‰ف‚ئ•ہ‚ٌ‚إ‚¢‚é
چd‰ف2–‡‚ج‚¤‚؟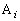 ڈم‚جچd‰ف‚ئ‚ح‹t‚ج–ت‚ًڈم‚ة‚µ‚½‚à‚ج‚ج–‡گ”‚ً ڈم‚جچd‰ف‚ئ‚ح‹t‚ج–ت‚ًڈم‚ة‚µ‚½‚à‚ج‚ج–‡گ”‚ً
k‚ئ‚·‚éپBژں‚ةپA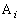 ڈم‚جچd‰ف‚ًٹm—¦ ڈم‚جچd‰ف‚ًٹm—¦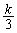 ‚إ‚ذ‚ء‚‚è•ش‚µپAٹm—¦ ‚إ‚ذ‚ء‚‚è•ش‚µپAٹm—¦
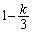 ‚إ‚»‚ج‚ـ‚ـ‚ة‚µ‚ؤ‚¨‚پB ‚إ‚»‚ج‚ـ‚ـ‚ة‚µ‚ؤ‚¨‚پB |
ˆب‰؛پAn‚ًژ©‘Rگ”‚ئ‚·‚éپB‘€چىT‚ًn‰ٌŒJ‚è•ش‚µچs‚ء‚½Œ‹‰تپA•\‚ًڈم‚ة‚µ‚½چd‰ف‚ھ‚؟‚ه‚¤‚ا1–‡‚¾‚¯‚ ‚éٹm—¦‚ً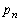 پC‚؟‚ه‚¤‚ا2–‡‚¾‚¯‚ ‚è‚»‚ê‚ç‚ھ•س‚ة‰ˆ‚ء‚ؤ•ہ‚ٌ‚إ‚¢‚éٹm—¦‚ً
پC‚؟‚ه‚¤‚ا2–‡‚¾‚¯‚ ‚è‚»‚ê‚ç‚ھ•س‚ة‰ˆ‚ء‚ؤ•ہ‚ٌ‚إ‚¢‚éٹm—¦‚ً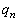 پC‚؟‚ه‚¤‚ا2–‡‚¾‚¯‚ ‚è‚»‚ê‚ç‚ھ‘خٹpگü‚ة‰ˆ‚ء‚ؤ•ہ‚ٌ‚إ‚¢‚éٹm—¦‚ً
پC‚؟‚ه‚¤‚ا2–‡‚¾‚¯‚ ‚è‚»‚ê‚ç‚ھ‘خٹpگü‚ة‰ˆ‚ء‚ؤ•ہ‚ٌ‚إ‚¢‚éٹm—¦‚ً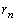 پC‚؟‚ه‚¤‚ا3–‡‚¾‚¯‚ ‚éٹm—¦‚ً
پC‚؟‚ه‚¤‚ا3–‡‚¾‚¯‚ ‚éٹm—¦‚ً ‚ئ‚·‚éپB
‚ئ‚·‚éپB
(2) 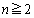 ‚ج‚ئ‚«پA
‚ج‚ئ‚«پA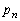 پC
پC پC
پC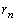 پC
پC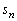 ‚ئ
‚ئ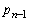 پC
پC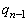 پC
پC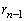 پC
پC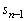 ‚جٹضŒW‚ً4ژں‚جگ³•ûچs—ٌ‚ً—p‚¢‚ؤ•\‚·‚ئپA
‚جٹضŒW‚ً4ژں‚جگ³•ûچs—ٌ‚ً—p‚¢‚ؤ•\‚·‚ئپA ‚إ‚ ‚éپB‚±‚ê‚و‚è”Cˆس‚جn‚ة‘خ‚µ‚ؤ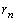 ‚ً‹پ‚ك‚é‚ئ
‚ً‹پ‚ك‚é‚ئ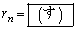 ‚إ‚ ‚éپB
‚إ‚ ‚éپB
(3) ”Cˆس‚جn‚ة‘خ‚µ‚ؤ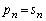 ‚إ‚ ‚邱‚ئ‚ًژ¦‚¹پB
‚إ‚ ‚邱‚ئ‚ًژ¦‚¹پB (4) ”Cˆس‚جn‚ة‘خ‚µ‚ؤ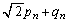 ‚ئ
‚ئ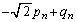 ‚ً‹پ‚ك‚é‚ئپA
‚ً‹پ‚ك‚é‚ئپA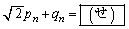 پC
پC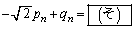 ‚إ‚ ‚éپB‚±‚ê‚و‚èپA
‚إ‚ ‚éپB‚±‚ê‚و‚èپA پC
پC ‚إ‚ ‚éپB
‚إ‚ ‚éپB [‰ً“ڑ‚ض]
–¼چH‘هگ”ٹw'08”N‘Oٹْ[4]
•\‚جڈo‚éٹm—¦‚ھp (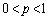 )پA— ‚جڈo‚éٹm—¦‚ھ
)پA— ‚جڈo‚éٹm—¦‚ھ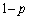 ‚جƒRƒCƒ“‚ً—p‚¢‚ؤپAˆب‰؛‚جژèڈ‡‚ة‚و‚è1‚آ‚ج‹َٹشƒxƒNƒgƒ‹‚ً’è‚ك‚éپB1‰ٌ–ع‚ةƒRƒCƒ“‚ً“ٹ‚°‚ؤپA•\‚ھڈo‚ê‚خxگ¬•ھ‚ً1پC— ‚ھڈo‚ê‚خxگ¬•ھ‚ً
‚جƒRƒCƒ“‚ً—p‚¢‚ؤپAˆب‰؛‚جژèڈ‡‚ة‚و‚è1‚آ‚ج‹َٹشƒxƒNƒgƒ‹‚ً’è‚ك‚éپB1‰ٌ–ع‚ةƒRƒCƒ“‚ً“ٹ‚°‚ؤپA•\‚ھڈo‚ê‚خxگ¬•ھ‚ً1پC— ‚ھڈo‚ê‚خxگ¬•ھ‚ً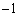 ‚ئ‚µپA2‰ٌ–ع‚ةƒRƒCƒ“‚ً“ٹ‚°‚ؤ“¯‚¶‚و‚¤‚ةyگ¬•ھ‚ًŒˆ‚كپA3‰ٌ–ع‚ةƒRƒCƒ“‚ً“ٹ‚°‚ؤ“¯‚¶‚و‚¤‚ةzگ¬•ھ‚ًŒˆ‚ك‚éپB‚±‚جژèڈ‡‚ً3‰ٌŒJ‚è•ش‚µ‚ؤپA3‚آ‚ج‹َٹشƒxƒNƒgƒ‹
‚ئ‚µپA2‰ٌ–ع‚ةƒRƒCƒ“‚ً“ٹ‚°‚ؤ“¯‚¶‚و‚¤‚ةyگ¬•ھ‚ًŒˆ‚كپA3‰ٌ–ع‚ةƒRƒCƒ“‚ً“ٹ‚°‚ؤ“¯‚¶‚و‚¤‚ةzگ¬•ھ‚ًŒˆ‚ك‚éپB‚±‚جژèڈ‡‚ً3‰ٌŒJ‚è•ش‚µ‚ؤپA3‚آ‚ج‹َٹشƒxƒNƒgƒ‹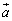 پC
پC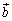 پC
پC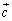 ‚ًŒˆ‚ك‚éپB
‚ًŒˆ‚ك‚éپB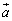 ‚ئ
‚ئ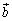 ‚جxگ¬•ھ‚ھ“¯•„چ†‚ئ‚ب‚éٹm—¦‚ًα‚ئ‚·‚éپB
‚جxگ¬•ھ‚ھ“¯•„چ†‚ئ‚ب‚éٹm—¦‚ًα‚ئ‚·‚éپB
(1) α‚ًp‚ً—p‚¢‚ؤ•\‚¹پB
(2) “àگد ‚ھ1‚ئ‚ب‚éٹm—¦‚ًα‚ً—p‚¢‚ؤ•\‚¹پB
‚ھ1‚ئ‚ب‚éٹm—¦‚ًα‚ً—p‚¢‚ؤ•\‚¹پB (3) “àگد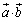 ‚جٹْ‘ز’l‚ًα‚ً—p‚¢‚ؤ•\‚¹پB
‚جٹْ‘ز’l‚ًα‚ً—p‚¢‚ؤ•\‚¹پB (4) 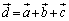 پC
پC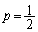 ‚ئ‚µ‚ؤ“àگد
‚ئ‚µ‚ؤ“àگد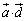 ‚ھگ³‚ئ‚ب‚éٹm—¦‚ً‹پ‚ك‚وپB
‚ھگ³‚ئ‚ب‚éٹm—¦‚ً‹پ‚ك‚وپB [‰ً“ڑ‚ض]
ŒQ”n‘هˆمگ”ٹw'09”N[2]
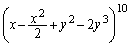 ‚ً“WٹJ‚µ‚ؤ“¾‚ç‚ê‚éxپCy‚ج‘½چ€ژ®‚ة‚آ‚¢‚ؤپAژںگ”‚ھ12‚إ‚ ‚éٹeچ€‚جŒWگ”‚جکa‚ً‹پ‚ك‚وپB
‚ً“WٹJ‚µ‚ؤ“¾‚ç‚ê‚éxپCy‚ج‘½چ€ژ®‚ة‚آ‚¢‚ؤپAژںگ”‚ھ12‚إ‚ ‚éٹeچ€‚جŒWگ”‚جکa‚ً‹پ‚ك‚وپB
[‰ً“ڑ‚ض]
‹م‘هگ”ٹw'10”N‘Oٹْ[2]
ژں‚ج‚و‚¤‚ب‹£‹Z‚ًچl‚¦‚éپB‹£‹Zژز‚ھƒTƒCƒRƒچ‚ًگU‚éپB‚à‚µپAڈo‚½–ع‚ھ‹C‚ة“ü‚ê‚خ‚»‚ج–ع‚ً“¾“_‚ئ‚·‚éپB‚»‚¤‚إ‚ب‚¯‚ê‚خپA‚à‚¤1‰ٌƒTƒCƒRƒچ‚ًگU‚ء‚ؤپA2‚آ‚ج–ع‚جچ‡Œv‚ً“¾“_‚ئ‚·‚邱‚ئ‚ھ‚إ‚«‚éپB‚½‚¾‚µپAچ‡Œv‚ھ7ˆبڈم‚ة‚ب‚ء‚½ڈêچ‡‚ح“¾“_‚ح0“_‚ئ‚·‚éپB‚±‚جژو‚茈‚ك‚ة‚و‚ء‚ؤپA2‰ٌ–ع‚ًگU‚é‚ئ“¾“_‚ھ‰؛‚ھ‚邱‚ئ‚à‚ ‚邱‚ئ‚ة’چˆس‚µ‚و‚¤پBژں‚ج–â‚¢‚ة“ڑ‚¦‚وپB
(1) ‹£‹Zژز‚ھڈي‚ةƒTƒCƒRƒچ‚ً2‰ٌگU‚é‚ئ‚·‚é‚ئپA“¾“_‚جٹْ‘ز’l‚ح‚¢‚‚ç‚©پB
(2) ‹£‹Zژز‚ھچإڈ‰‚ج–ع‚ھ6‚ج‚ئ‚«‚¾‚¯2‰ٌ–ع‚ًگU‚ç‚ب‚¢‚ئ‚·‚é‚ئپA“¾“_‚جٹْ‘ز’l‚ح‚¢‚‚ç‚©پB
(3) “¾“_‚جٹْ‘ز’l‚ًچإ‘ه‚ة‚·‚邽‚ك‚ة‚حپA‹£‹Zژز‚حچإڈ‰‚ج–ع‚ھ‚ا‚ج”حˆح‚ة‚ ‚é‚ئ‚«‚ة2‰ٌ–ع‚ً‚س‚é‚ئ‚و‚¢‚©پB
[‰ً“ڑ‚ض]
ŒF–{‘هˆمگ”ٹw'10”N[2]
گش‹…4Œآ‚ئ”’‹…6Œآ‚ج“ü‚ء‚½‘ـ‚©‚ç2Œآ‚ج‹…‚ً“¯ژ‚ةژو‚èڈo‚µپA‚»‚ج’†‚ةگش‹…‚ھٹـ‚ـ‚ê‚ؤ‚¢‚½‚çپA‚»‚جŒآگ”‚¾‚¯‚³‚ç‚ة‘ـ‚©‚ç‹…‚ًژو‚èڈo‚·پB‚±‚ج‚ئ‚«پAˆب‰؛‚ج–â‚¢‚ة“ڑ‚¦‚وپB
(–â1)پ@ژو‚èڈo‚µ‚½گش‹…‚ج‘چگ”‚ھ2‚إ‚ ‚éٹm—¦‚ً‹پ‚ك‚وپB
(–â2)پ@ژو‚èڈo‚µ‚½گش‹…‚ج‘چگ”‚ھپAژو‚èڈo‚µ‚½”’‹…‚ج‘چگ”‚ً‰z‚¦‚éٹm—¦‚ً‹پ‚ك‚وپB
[‰ً“ڑ‚ض]
‹م‘هگ”ٹw'10”NŒمٹْ[4]
•\‚ئ— ‚جڈo‚éٹm—¦‚ھ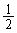 ‚¸‚آ‚جچd‰ف‚ً“ٹ‚°پA•\‚ب‚ç1“_پA— ‚ب‚ç0“_‚ئ‚·‚éپBkپCn‚ًگ³‚جگ®گ”‚ئ‚µ‚ؤپAˆب‰؛‚ج–â‚¢‚ة“ڑ‚¦‚وپB
‚¸‚آ‚جچd‰ف‚ً“ٹ‚°پA•\‚ب‚ç1“_پA— ‚ب‚ç0“_‚ئ‚·‚éپBkپCn‚ًگ³‚جگ®گ”‚ئ‚µ‚ؤپAˆب‰؛‚ج–â‚¢‚ة“ڑ‚¦‚وپB
1پDچd‰ف‚ًŒJ‚è•ش‚µ‚ؤ“ٹ‚°پA“¾“_‚جچ‡Œv‚ھ3“_‚ة’B‚µ‚½‚çڈI—¹‚·‚邱‚ئ‚ة‚·‚éپB‚؟‚ه‚¤‚ا5‰ٌ–ع‚إڈI—¹‚·‚éٹm—¦‚ح‚¢‚‚ç‚©پB‚ـ‚½پA‚؟‚ه‚¤‚اn‰ٌ–ع‚إڈI—¹‚·‚éٹm—¦‚ً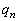 ‚ئ‚·‚é‚ئ‚«پA
‚ئ‚·‚é‚ئ‚«پA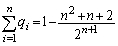 ‚ًڈط–¾‚¹‚وپB
‚ًڈط–¾‚¹‚وپB 2پDچd‰ف‚ًŒJ‚è•ش‚µ‚ؤ“ٹ‚°پA“¾“_‚جچ‡Œv‚ھk“_‚ة’B‚µ‚½‚çڈI—¹‚·‚邱‚ئ‚ة‚·‚éپB‚؟‚ه‚¤‚اn‰ٌ–ع‚إڈI—¹‚·‚éٹm—¦‚ً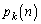 ‚ئ‚·‚éپBk‚ًŒإ’肵‚½‚ـ‚ـn‚ً“®‚©‚·‚ئ‚«‚ج
‚ئ‚·‚éپBk‚ًŒإ’肵‚½‚ـ‚ـn‚ً“®‚©‚·‚ئ‚«‚ج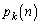 ‚جچإ‘ه’l‚ً‹پ‚ك‚وپB
‚جچإ‘ه’l‚ً‹پ‚ك‚وپB [‰ً“ڑ‚ض]
‹م‘هگ”ٹw'11”N‘Oٹْ[5]
1‚©‚ç4‚ـ‚إ‚جگ”ژڑ‚ھ1‚آ‚¸‚آڈ‘‚©‚ꂽ4–‡‚جƒJپ[ƒh‚ھ‚ ‚éپB‚»‚ج4–‡‚جƒJپ[ƒh‚ً‰،ˆê—ٌ‚ة•ہ‚×پAˆب‰؛‚ج‘€چى‚ًچl‚¦‚éپB
‘€چىپF1‚©‚ç4‚ـ‚إ‚جگ”ژڑ‚ھ1‚آ‚¸‚آڈ‘‚©‚ꂽ4Œآ‚ج‹…‚ھ“ü‚ء‚ؤ‚¢‚é‘ـ‚©‚瓯ژ‚ة2Œآ‚ج‹…‚ًژو‚èڈo‚·پB‹…‚ةڈ‘‚©‚ꂽگ”ژڑ‚ھi‚ئj‚ب‚ç‚خپAi‚جƒJپ[ƒh‚ئj‚جƒJپ[ƒh‚ً“ü‚ê‘ض‚¦‚éپB‚»‚جŒمپA2Œآ‚ج‹…‚ح‘ـ‚ة–ك‚·پB
‚ح‚¶‚ك‚ةƒJپ[ƒh‚ًچ¶‚©‚çڈ‡‚ة1پC2پC3پC4‚ئ•ہ‚×پAڈم‚ج‘€چى‚ًn‰ٌŒJ‚è•ش‚µ‚½Œم‚جƒJپ[ƒh‚ة‚آ‚¢‚ؤپAˆب‰؛‚ج–â‚¢‚ة“ڑ‚¦‚وپB
(1) 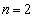 ‚ج‚ئ‚«پAƒJپ[ƒh‚ھچ¶‚©‚çڈ‡‚ة1پC2پC3پC4‚ئ•ہ‚شٹm—¦‚ً‹پ‚ك‚وپB
‚ج‚ئ‚«پAƒJپ[ƒh‚ھچ¶‚©‚çڈ‡‚ة1پC2پC3پC4‚ئ•ہ‚شٹm—¦‚ً‹پ‚ك‚وپB (2) 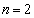 ‚ج‚ئ‚«پAƒJپ[ƒh‚ھچ¶‚©‚çڈ‡‚ة4پC3پC2پC1‚ئ•ہ‚شٹm—¦‚ً‹پ‚ك‚وپB
‚ج‚ئ‚«پAƒJپ[ƒh‚ھچ¶‚©‚çڈ‡‚ة4پC3پC2پC1‚ئ•ہ‚شٹm—¦‚ً‹پ‚ك‚وپB (3) 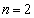 ‚ج‚ئ‚«پAچ¶’[‚جƒJپ[ƒh‚جگ”ژڑ‚ھ1‚ة‚ب‚éٹm—¦‚ً‹پ‚ك‚وپB
‚ج‚ئ‚«پAچ¶’[‚جƒJپ[ƒh‚جگ”ژڑ‚ھ1‚ة‚ب‚éٹm—¦‚ً‹پ‚ك‚وپB (4) 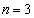 ‚ج‚ئ‚«پAچ¶’[‚جƒJپ[ƒh‚جگ”ژڑ‚جٹْ‘ز’l‚ً‹پ‚ك‚وپB
‚ج‚ئ‚«پAچ¶’[‚جƒJپ[ƒh‚جگ”ژڑ‚جٹْ‘ز’l‚ً‹پ‚ك‚وپB [‰ً“ڑ‚ض]
“Œ–k‘ه—Œnگ”ٹw'11”N‘Oٹْ[3]
گوگ¶‚ئ3گl‚جگ¶“kAپCBپCC‚ھ‚¨‚èپA‹ت‚ج“ü‚ء‚½” ‚ھ‚ ‚éپB” ‚ج’†‚ة‚حچإڈ‰پAگش‹ت3ŒآپA”’‹ت7ŒآپA‘S•”‚إ10Œآ‚ج‹ت‚ھ“ü‚ء‚ؤ‚¢‚éپBگوگ¶‚ھƒTƒCƒRƒچ‚ً‚س‚ء‚ؤپA1‚ج–ع‚ھڈo‚½‚çA‚ھپA2‚ـ‚½‚ح3‚ج–ع‚ھڈo‚½‚çB‚ھپA‚»‚ج‘¼‚ج–ع‚ھڈo‚½‚çC‚ھ” ‚ج’†‚©‚ç1‚آ‚¾‚¯‹ت‚ًژو‚èڈo‚·‘€چى‚ًچs‚¤پBژو‚èڈo‚µ‚½‹ت‚ح” ‚ج’†‚ة–ك‚³‚¸پAژو‚èڈo‚µ‚½گ¶“k‚ج‚à‚ج‚ئ‚·‚éپB‚±‚ج‘€چى‚ً‘±‚¯‚ؤچs‚¤‚à‚ج‚ئ‚µ‚ؤˆب‰؛‚ج–â‚¢‚ة“ڑ‚¦‚وپB
‚½‚¾‚µپAƒTƒCƒRƒچ‚ج1‚©‚ç6‚ج–ع‚جڈo‚éٹm—¦‚ح“™‚µ‚¢‚à‚ج‚ئ‚µپA‚ـ‚½پA” ‚ج’†‚ج‚»‚ꂼ‚ê‚ج‹ت‚جژو‚èڈo‚³‚ê‚éٹm—¦‚ح“™‚µ‚¢‚à‚ج‚ئ‚·‚éپB
(1) 2‰ٌ–ع‚ج‘€چى‚ھڈI‚ي‚ء‚½‚ئ‚«پAA‚ھ2Œآ‚جگش‹ت‚ًژè‚ة“ü‚ê‚ؤ‚¢‚éٹm—¦‚ً‹پ‚ك‚وپB
(2) 2‰ٌ–ع‚ج‘€چى‚ھڈI‚ي‚ء‚½‚ئ‚«پAB‚ھڈ‚ب‚‚ئ‚à1Œآ‚جگش‹ت‚ًژè‚ة“ü‚ê‚ؤ‚¢‚éٹm—¦‚ً‹پ‚ك‚وپB
(3) 3‰ٌ–ع‚ج‘€چى‚إپAC‚ھگش‹ت‚ًژو‚èڈo‚·ٹm—¦‚ً‹پ‚ك‚وپB
[‰ً“ڑ‚ض]
پyچLچگپz‚±‚±‚©‚çچLچگ‚إ‚·پB‚²——‚جٹF‚³‚ـ‚ج‚²ژx‰‡‚²—‰ً‚ًژ’‚肽‚پA‚و‚낵‚‚¨ٹè‚¢‚¢‚½‚µ‚ـ‚·پB
پyچLچگپzچLچگ‚ح‚±‚±‚ـ‚إ‚إ‚·پB
پ@پ@گ”ٹwTOPپ@پ@TOPƒyپ[ƒW‚ة–ك‚é
پyچLچگپz‚±‚±‚©‚çچLچگ‚إ‚·پB‚²——‚جٹF‚³‚ـ‚ج‚²ژx‰‡‚²—‰ً‚ًژ’‚肽‚پA‚و‚낵‚‚¨ٹè‚¢‚¢‚½‚µ‚ـ‚·پB
پyچLچگپzچLچگ‚ح‚±‚±‚ـ‚إ‚إ‚·پB
‹êٹwٹyٹwڈm گڈژ“ü‰ïژَ•t’†پI—Œn‘هٹwژَŒ±ƒlƒbƒgڈm‹êٹwٹyٹwڈm(‚²ˆؤ“à‚ح‚±‚؟‚ç)‚²“ü‰ï‚حپA
‚ـ‚¸پA‚±‚؟‚ç‚ـ‚إƒپپ[ƒ‹‚ً
‚¨‘—‚è‚‚¾‚³‚¢پB