いろいろな曲線演習問題
名工大数学'09年[2]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
楕円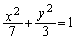 を原点を中心に反時計回りに角
を原点を中心に反時計回りに角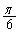 だけ回転して得られる曲線をCとする。
だけ回転して得られる曲線をCとする。
(1) 曲線Cの方程式を求めよ。
(2) 直線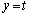 がCと共有点を持つような実数tの範囲を求めよ。
がCと共有点を持つような実数tの範囲を求めよ。 (3) すべての頂点がC上にあり、1辺がx軸に平行な三角形の面積の最大値を求めよ。
[解答へ]
北大理系数学'07年前期[5]
楕円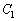 :
: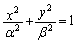 と双曲線
と双曲線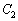 :
: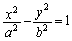 を考える。
を考える。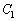 と
と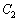 の焦点が一致しているならば、
の焦点が一致しているならば、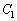 と
と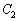 の交点でそれぞれの接線は直交することを示せ。
の交点でそれぞれの接線は直交することを示せ。
[解答へ]
名大理系数学'09年前期[1]
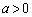 ,
,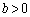 とする。点A
とする。点A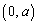 を中心とする半径rの円が、双曲線
を中心とする半径rの円が、双曲線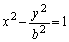 と2点B
と2点B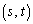 ,C
,C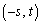 で接しているとする。ただし、
で接しているとする。ただし、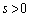 とする。ここで、双曲線と円が点Pで接するとは、Pが双曲線と円との共有点であり、かつ点Pにおける双曲線の接線と点Pにおける円の接線が一致することである。
とする。ここで、双曲線と円が点Pで接するとは、Pが双曲線と円との共有点であり、かつ点Pにおける双曲線の接線と点Pにおける円の接線が一致することである。
(1) r,s,tをaとbを用いて表せ。
(2) △ABCが正三角形となるaとrが存在するようなbの値の範囲を求めよ。
[解答へ]
慶大医数学'09年[2]
以下の文章の空欄に適切な数または式を入れて文章を完成させなさい。
a,bを正の定数、mを実数、kを負の実数とする。xy平面上の楕円C: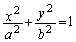 と直線l:
と直線l: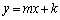 が異なる2点P,Qで交わるための必要十分条件は
が異なる2点P,Qで交わるための必要十分条件は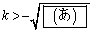 であり、このとき、
であり、このとき、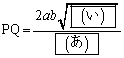 である。さらに、点P,Qを固定して点Rを楕円C上で動かすときの
である。さらに、点P,Qを固定して点Rを楕円C上で動かすときの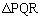 の面積の最大値をAとすると
の面積の最大値をAとすると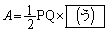 である。次に、mを固定してkを動かすとき、Aが最大となるkの値は
である。次に、mを固定してkを動かすとき、Aが最大となるkの値は であり、その最大値は
であり、その最大値は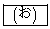 である。
である。
[解答へ]
福井大医数学'08年[2]
座標平面において、原点Oを中心とする半径1の円C上に点P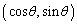 をとり、PにおけるCの接線lと直線
をとり、PにおけるCの接線lと直線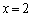 の交点をQとおく。ただし、
の交点をQとおく。ただし、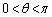 とする。l上の点Rが
とする。l上の点Rが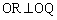 を満たすとき、以下の問いに答えよ。
を満たすとき、以下の問いに答えよ。
(1) Rの座標をθ を用いて表せ。
(2) θ が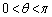 の範囲を動くとき、線分PRの長さの最大値とそのときのθ の値を求めよ。
の範囲を動くとき、線分PRの長さの最大値とそのときのθ の値を求めよ。 (3) θ が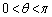 の範囲を動くときのRの軌跡を求め、その概形を描け。
の範囲を動くときのRの軌跡を求め、その概形を描け。 [解答へ]
筑波大数学'08年[6]
放物線C: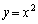 上の異なる2点P
上の異なる2点P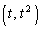 ,Q
,Q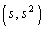 (
(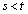 )における接線の交点をR
)における接線の交点をR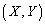 とする。
とする。
(1) X,Yをt,sを用いて表せ。
(2) 点P,Qが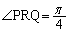 を満たしながらC上を動くとき、点Rは双曲線上を動くことを示し、かつ、その双曲線の方程式を求めよ。
を満たしながらC上を動くとき、点Rは双曲線上を動くことを示し、かつ、その双曲線の方程式を求めよ。 [解答へ]
同志社大理工数学'09年[4]
双曲線C: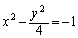 について次の問いに答えよ。
について次の問いに答えよ。
(1) Cの漸近線の方程式を記せ。
(2) mを任意の実数として、直線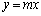 が曲線Cに接していないことを示せ。
が曲線Cに接していないことを示せ。 (3) 点A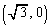 を通るCの接線の方程式をすべて求めよ。
を通るCの接線の方程式をすべて求めよ。 (4) C上にない点P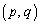 を通るCの接線がちょうど2本あって、2本の接線が直交するとき、p,qがみたすべき条件を求めよ。
を通るCの接線がちょうど2本あって、2本の接線が直交するとき、p,qがみたすべき条件を求めよ。 [解答へ]
東工大数学'09年後期[1]
aが与えられた実数のとき、xyz空間の点C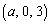 から出た光が球
から出た光が球
でさえぎられてできるxy平面上の影をSとする。点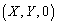 がSに含まれる条件を求めよ。
がSに含まれる条件を求めよ。
[解答へ]
横浜国大工数学'09年後期[3]
xy平面上の領域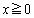 ,
,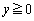 で、方程式
で、方程式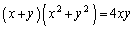 が表す曲線をCとする。正の数tに対して、直線
が表す曲線をCとする。正の数tに対して、直線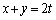 がCと異なる2点Q,Rで交わるとき、次の問いに答えよ。
がCと異なる2点Q,Rで交わるとき、次の問いに答えよ。
(1) Cを極座標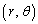 に関する方程式で表し、rのとり得る値の最大値を求めよ。
に関する方程式で表し、rのとり得る値の最大値を求めよ。 (2) Q,Rの座標をtを用いて表せ。
(3) 線分QRの長さが最大となるtの値を求めよ。
[解答へ]
横浜国大工数学'10年前期[4]
a,bを正の実数とする。曲線
C: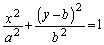
は領域D: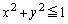 に含まれている。次の問いに答えよ。
に含まれている。次の問いに答えよ。
(1) 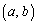 が存在する範囲をab平面上に図示せよ。
が存在する範囲をab平面上に図示せよ。 (2) Cが囲む部分の面積が最大になるときのa,bの値を求めよ。
[解答へ]
阪大理系数学'10年前期[2]
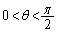 とする。2つの曲線
とする。2つの曲線
の交点のうち、x座標とy座標がともに正であるものをPとする。Pにおける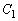 ,
,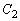 の接線をそれぞれ
の接線をそれぞれ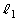 ,
,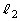 とし、y軸と
とし、y軸と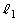 ,
,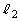 の交点をそれぞれQ,Rとする。θ が
の交点をそれぞれQ,Rとする。θ が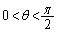 の範囲を動くとき、線分QRの長さの最小値を求めよ。
の範囲を動くとき、線分QRの長さの最小値を求めよ。
[解答へ]
岐阜薬大数学'10年[6]
楕円O: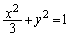 ,直線l:
,直線l: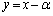 (
(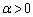 ),直線
),直線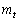 :
: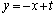 がある。楕円Oと直線lが接しているとき、次の問いに答えよ。
がある。楕円Oと直線lが接しているとき、次の問いに答えよ。
(1) αの値を求めよ。また、楕円Oと直線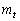 が2個の共有点をもつように、tの値の存在範囲を求めよ。
が2個の共有点をもつように、tの値の存在範囲を求めよ。 (2) 直線lと直線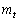 の交点を点Hとするとき、点A
の交点を点Hとするとき、点A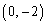 と点Hとの距離sをtを用いて表せ。また、楕円Oと直線
と点Hとの距離sをtを用いて表せ。また、楕円Oと直線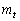 が2個の共有点P,Qをもつとき、
が2個の共有点P,Qをもつとき、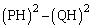 をtを用いて表せ。ただし、
をtを用いて表せ。ただし、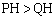 とする。
とする。 (3) 楕円Oを直線lのまわりに1回転してできる回転体の体積Vを求めよ。
[解答へ]
京都府立医大数学'10年[1]
Oを原点とする座標平面上の楕円C: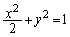 を考える。
を考える。
点P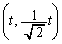 (ただし、
(ただし、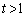 )を通る楕円Cの2つの接線を
)を通る楕円Cの2つの接線を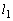 ,
,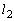 とし、それらと楕円との接点をそれぞれQ,Rとする。点Qを通り
とし、それらと楕円との接点をそれぞれQ,Rとする。点Qを通り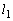 と直交する直線を
と直交する直線を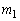 とし、点Rを通り
とし、点Rを通り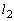 と直交する直線を
と直交する直線を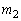 とする。直線
とする。直線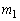 と
と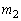 の交点をSとする。ただし、Qのx座標はRのx座標より大きいとする。
の交点をSとする。ただし、Qのx座標はRのx座標より大きいとする。
(1) 2点Q,Rの座標をt を用いて表せ。
(2) 点Sの座標をt を用いて表せ。
(3) t が1より大きい実数全体を動くとき、点Sの軌跡を求めよ。
(4) 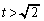 であるとき、△OPSの面積を
であるとき、△OPSの面積を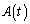 とする。
とする。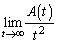 を求めよ。
を求めよ。 [解答へ]
鹿児島大数学'10年[6]
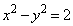 で表される曲線をCとし、P
で表される曲線をCとし、P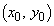 をC上の点とする。次の各問いに答えよ。
をC上の点とする。次の各問いに答えよ。
(1) 曲線C上の点Pにおける接線lの方程式は、
となることを証明せよ。
(2) 原点Oからlにおろした垂線をOHとする。Hの座標を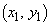 とするとき、
とするとき、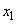 ,
,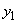 を
を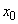 ,
,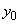 で表せ。
で表せ。 (3) F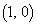 ,
,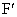
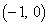 とする。
とする。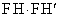 は点Pの取り方によらず一定であることを証明せよ。また、その値を求めよ。
は点Pの取り方によらず一定であることを証明せよ。また、その値を求めよ。 [解答へ]
電通大数学'11年前期[4]
直線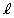 :
: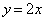 の法線ベクトルを
の法線ベクトルを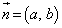 とし、点P
とし、点P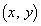 と直線
と直線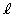 との距離をhとする。ただし、
との距離をhとする。ただし、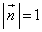 で、
で、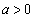 とする。
とする。
以下の問いに答えよ。
(1) 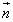 の成分a,bを求めよ。
の成分a,bを求めよ。 (2) 原点をOとし、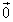 でない
でない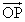 に対し、
に対し、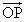 と
と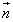 のなす角をθ とする。
のなす角をθ とする。 このとき、hを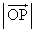 とθ を用いて表せ。また、hをx,yを用いて表せ。
とθ を用いて表せ。また、hをx,yを用いて表せ。 以下では、曲線Cを、点A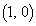 と直線
と直線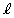 からの距離が等しい点P
からの距離が等しい点P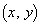 の軌跡とする。
の軌跡とする。
(3) 曲線Cの方程式(x,yの関係式)を求めよ。
(4) 曲線Cと直線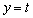 (t は定数)との共有点の個数を求めよ。
(t は定数)との共有点の個数を求めよ。 (5) 曲線Cと直線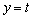 が2個の共有点Q,Rをもつとき、線分QRの長さをt を用いて表せ。
が2個の共有点Q,Rをもつとき、線分QRの長さをt を用いて表せ。 (6) 曲線Cと直線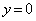 とで囲まれる部分の面積Sを求めよ。
とで囲まれる部分の面積Sを求めよ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。  である。さらに、点P,Qを固定して点Rを楕円C上で動かすときの
である。さらに、点P,Qを固定して点Rを楕円C上で動かすときの