阪大物理'25年前期[1]
水平な床の上を運動する台と、台の上にのせた小物体について考察する。台および小物体はx軸に沿ってのみ運動するものとする。重力加速度の大きさは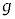 である。加速度の正の向きはx軸の正の向きとする。
である。加速度の正の向きはx軸の正の向きとする。
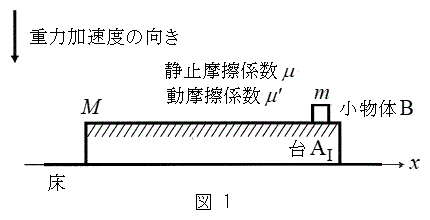 Ⅰ.図1のように、水平な床の上に質量Mの台
Ⅰ.図1のように、水平な床の上に質量Mの台 を静止させ、台
を静止させ、台 の上に質量mの小物体Bを静止させた。台
の上に質量mの小物体Bを静止させた。台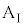 と小物体Bの間には摩擦があり、その静止摩擦係数はμ,動摩擦係数は
と小物体Bの間には摩擦があり、その静止摩擦係数はμ,動摩擦係数は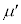 (ただし
(ただし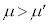 )である。床と台
)である。床と台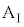 の間には摩擦はないものとする。また、小物体Bをのせた台
の間には摩擦はないものとする。また、小物体Bをのせた台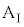 の面は水平である。なお、台
の面は水平である。なお、台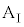 の長さは十分に長く、小物体Bは台
の長さは十分に長く、小物体Bは台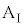 の上から滑り落ちないものとする。
の上から滑り落ちないものとする。時刻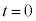 から、台
から、台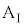 に対してx軸の正の向きに大きさが
に対してx軸の正の向きに大きさが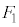 の一定の力を加え続けた。
の一定の力を加え続けた。
問1 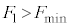 のとき、小物体Bは台
のとき、小物体Bは台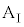 に対してすべるように運動した。また、
に対してすべるように運動した。また、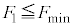 のとき、台
のとき、台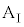 と小物体Bは一体となって運動した。
と小物体Bは一体となって運動した。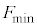 を、
を、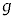 ,M,m,μ,
,M,m,μ,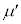 のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。
問2 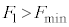 のとき、時刻
のとき、時刻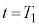 (
(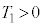 )における、台
)における、台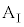 の速度
の速度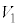 と小物体Bの速度
と小物体Bの速度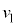 を、
を、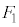 ,
,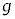 ,M,m,
,M,m,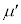 ,
,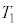 のうち必要なものを用いてそれぞれ表せ。
のうち必要なものを用いてそれぞれ表せ。
 Ⅱ.図2のように、両端に壁をもつ質量Mの台
Ⅱ.図2のように、両端に壁をもつ質量Mの台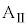 を水平な床の上に静止させ、台
を水平な床の上に静止させ、台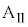 の上に質量mの小物体Bを静止させた。台
の上に質量mの小物体Bを静止させた。台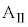 の壁と小物体Bとの間の反発係数(はねかえり係数)をeとし、
の壁と小物体Bとの間の反発係数(はねかえり係数)をeとし、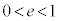 が満たされているとする。台
が満たされているとする。台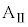 と小物体Bの間、および、床と台
と小物体Bの間、および、床と台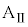 の間に摩擦はないものとする。また、小物体Bをのせた台
の間に摩擦はないものとする。また、小物体Bをのせた台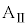 の面は水平である。
の面は水平である。時刻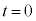 から時刻
から時刻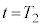 (
( )までの間、台
)までの間、台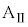 に対してx軸の正の向きに大きさが
に対してx軸の正の向きに大きさが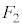 の一定の力を加え続けた。時刻
の一定の力を加え続けた。時刻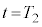 での、台
での、台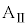 と小物体Bの速度はそれぞれ
と小物体Bの速度はそれぞれ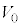 と
と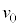 であった。なお、この間に、小物体Bは台
であった。なお、この間に、小物体Bは台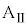 の壁に衝突することはなかった。
の壁に衝突することはなかった。
問3 小物体Bの速度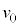 および時刻
および時刻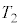 を、
を、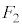 ,M,m,
,M,m,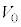 のうち必要なものを用いてそれぞれ表せ。
のうち必要なものを用いてそれぞれ表せ。 時刻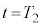 において、台
において、台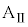 に対して力を加えることをやめた。その後、小物体Bは台
に対して力を加えることをやめた。その後、小物体Bは台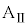 の壁と衝突を繰り返した。
の壁と衝突を繰り返した。
問4 十分に長い時間、衝突を繰り返した結果、台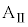 と小物体Bの速度はどちらも
と小物体Bの速度はどちらも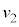 となった。速度
となった。速度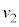 を、e,
を、e,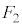 ,M,m,
,M,m,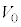 のうち必要なものを用いてそれぞれ表せ。
のうち必要なものを用いてそれぞれ表せ。
問5 小物体Bと壁がn回目の衝突をした直後の、台 の速度
の速度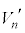 および小物体Bの速度
および小物体Bの速度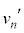 を、e,
を、e,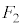 ,M,m,n,
,M,m,n,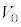 のうち必要なものを用いてそれぞれ表せ。ただし、nは1以上の整数とする。
のうち必要なものを用いてそれぞれ表せ。ただし、nは1以上の整数とする。
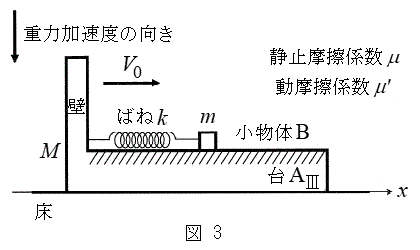 Ⅲ.図3のように、水平な床の上に質量Mの台
Ⅲ.図3のように、水平な床の上に質量Mの台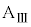 を静止させ、台
を静止させ、台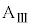 の上に質量mの小物体Bを静止させた。さらに、台
の上に質量mの小物体Bを静止させた。さらに、台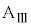 の壁と小物体Bを、質量の無視できるばね定数kのばねでつないだ。台
の壁と小物体Bを、質量の無視できるばね定数kのばねでつないだ。台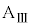 と小物体Bとの間には摩擦があり、その静止摩擦係数はμ,動摩擦係数は
と小物体Bとの間には摩擦があり、その静止摩擦係数はμ,動摩擦係数は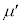 (ただし、
(ただし、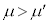 )とする。床と台
)とする。床と台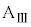 の間には摩擦はないものとする。また、小物体Bをのせた台
の間には摩擦はないものとする。また、小物体Bをのせた台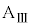 の面は水平である。
の面は水平である。最初、ばねの長さは自然長dであった。台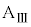 に対して、x軸の正の向きに瞬間的な力を加えたところ、その直後の台
に対して、x軸の正の向きに瞬間的な力を加えたところ、その直後の台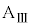 の速度は
の速度は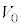 となり、小物体Bは台
となり、小物体Bは台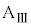 の上をすべりはじめた。しばらくの間、ばねは伸び縮みを繰り返し、その後、ばねの長さはLとなり変化しなくなった。また、このときの台
の上をすべりはじめた。しばらくの間、ばねは伸び縮みを繰り返し、その後、ばねの長さはLとなり変化しなくなった。また、このときの台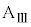 と小物体Bの速度はともに
と小物体Bの速度はともに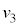 であった。なお、この運動の間、小物体Bは台
であった。なお、この運動の間、小物体Bは台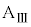 の壁に衝突したり、台
の壁に衝突したり、台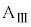 の上からすべり落ちることはなかった。
の上からすべり落ちることはなかった。
問6 速度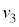 を、d,
を、d,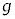 ,k,M,m,
,k,M,m,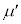 ,
, のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。
問7 小物体Bが台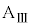 の上をすべり始めてからばねの長さが変化しなくなるまでの間に、小物体Bが台
の上をすべり始めてからばねの長さが変化しなくなるまでの間に、小物体Bが台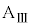 の上をすべった総距離をd,
の上をすべった総距離をd,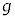 ,k,L,M,m,
,k,L,M,m,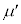 ,
,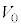 のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。 台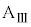 が速度
が速度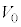 を得てから、ばねの長さがLとなり変化しなくなるまでの間の、小物体Bの運動について考察する。小物体Bが台
を得てから、ばねの長さがLとなり変化しなくなるまでの間の、小物体Bの運動について考察する。小物体Bが台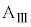 の上をすべりはじめると、ばねは縮みはじめた。ばねの長さが
の上をすべりはじめると、ばねは縮みはじめた。ばねの長さが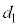 となったとき、小物体Bは台
となったとき、小物体Bは台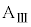 の上で1回目の折り返しを行い、ばねは伸び始めた。その後、ばねの長さが
の上で1回目の折り返しを行い、ばねは伸び始めた。その後、ばねの長さが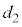 となったとき、小物体Bは台
となったとき、小物体Bは台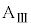 の上で2回目の折り返しを行い、ばねは再び縮みはじめた。以後、ばねはこのような伸び縮みを繰り返した。小物体Bは台
の上で2回目の折り返しを行い、ばねは再び縮みはじめた。以後、ばねはこのような伸び縮みを繰り返した。小物体Bは台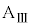 の上でn回目の折り返しを行ったのち、
の上でn回目の折り返しを行ったのち、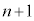 回目の折り返しをすることなく、台
回目の折り返しをすることなく、台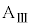 に対する運動を停止した。そしてそれ以降、ばねの長さは変化しなくなった。ここで、nは3以上の整数とする。
に対する運動を停止した。そしてそれ以降、ばねの長さは変化しなくなった。ここで、nは3以上の整数とする。
問8 台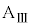 が速度
が速度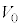 を得てから小物体Bが1回目の折り返しをするまでの間の運動を考える。その間のある時刻において、ばねの長さはDであった。その時刻における、台
を得てから小物体Bが1回目の折り返しをするまでの間の運動を考える。その間のある時刻において、ばねの長さはDであった。その時刻における、台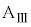 とともに運動する観測者からみた小物体Bの加速度aを、D,d,
とともに運動する観測者からみた小物体Bの加速度aを、D,d, ,k,M,m,
,k,M,m,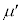 ,
,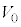 のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。
問9 1回目の折り返しの時点でのばねの長さ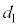 を、d,
を、d,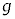 ,k,M,m,
,k,M,m,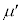 ,
,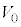 のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。 問10 小物体Bが台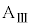 に対して運動を停止した後のばねの長さLを、d,
に対して運動を停止した後のばねの長さLを、d,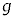 ,k,M,m,
,k,M,m,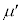 ,n,
,n,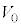 のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 力学全般にわたる総合問題です。難問というわけではないのですが、要求されているものが多く、問9,問10など無理です。
Ⅰ.問1 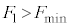 のときにすべり、
のときにすべり、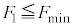 のときに台
のときに台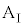 と小物体Bが一体となって運動した、ということは、
と小物体Bが一体となって運動した、ということは、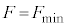 のときに滑り出す限界で台
のときに滑り出す限界で台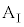 と小物体Bとの間の摩擦力fが最大静止力
と小物体Bとの間の摩擦力fが最大静止力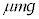 になっていて滑り出していない、台
になっていて滑り出していない、台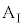 と小物体Bは一体となって運動している、ということです。つまり、台
と小物体Bは一体となって運動している、ということです。つまり、台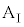 と小物体Bは同じ加速度aで等加速度運動します。このとき、小物体Bが受ける力はx軸正方向の最大静止摩擦力
と小物体Bは同じ加速度aで等加速度運動します。このとき、小物体Bが受ける力はx軸正方向の最大静止摩擦力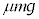 ,台
,台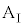 が受ける力はx軸正方向の
が受ける力はx軸正方向の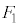 とx軸負方向の最大静止摩擦力
とx軸負方向の最大静止摩擦力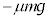 です。
です。 小物体の運動方程式: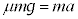 ・・・①
・・・①
台 の運動方程式:
の運動方程式: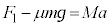 ・・・②
・・・② ①より、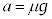
①+②より、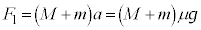
このとき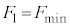 なので、
なので、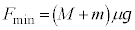 ......[答]
......[答]
問2 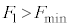 のときには、小物体Bと台
のときには、小物体Bと台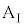 の間がすべり、両者の間に動摩擦力
の間がすべり、両者の間に動摩擦力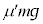 が働き、両者の加速度が異なります。小物体の加速度を
が働き、両者の加速度が異なります。小物体の加速度を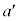 ,台
,台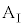 の加速度を
の加速度を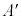 として、
として、 これより、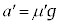 ,
,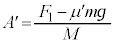
よって、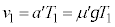 ......[答],
......[答],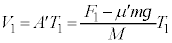 ......[答]
......[答]
Ⅱ.問3 台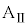 と小物体Bの間に摩擦がないので、台
と小物体Bの間に摩擦がないので、台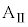 に力を加えて台
に力を加えて台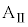 が動き出しても、小物体Bは動きません。
が動き出しても、小物体Bは動きません。 ......[答]
......[答] 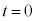 における系の運動量は0,
における系の運動量は0,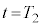 における系の運動量は
における系の運動量は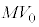 ,その間に系に及ぼされる力積は
,その間に系に及ぼされる力積は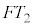 です。運動量の原理より、
です。運動量の原理より、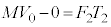 ∴
∴ 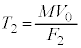 ......[答]
......[答]
問4 台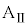 に対して力を加えることをやめると、以後、台
に対して力を加えることをやめると、以後、台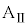 は速度
は速度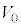 で等速度運動します。十分に長い時間経過後の系の運動量は
で等速度運動します。十分に長い時間経過後の系の運動量は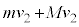 です。系には外力が働かないので、
です。系には外力が働かないので、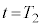 と、十分に長い時間経過後との運動量保存より、
と、十分に長い時間経過後との運動量保存より、 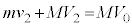 ∴
∴ 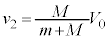 ......[答]
......[答]
問5 問4により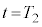 における系の運動量は
における系の運動量は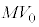 です。n回目の衝突後の系の運動量は
です。n回目の衝突後の系の運動量は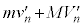 です。n回目の衝突後と
です。n回目の衝突後と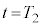 との運動量保存より、
との運動量保存より、 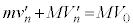 ・・・③
・・・③∴  ・・・④
・・・④
④を③に代入して、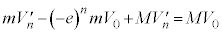
∴ 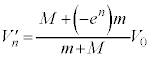 ......[答]④より、
......[答]④より、 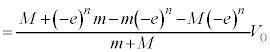
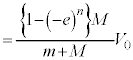 ......[答]
......[答]
Ⅲ.問6 瞬間的な力を加えた直後の台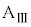 と小物体Bとばねからなる系の運動量は
と小物体Bとばねからなる系の運動量は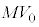 です。ばねの長さがLとなり変化しなくなった後の系の運動量は
です。ばねの長さがLとなり変化しなくなった後の系の運動量は です。系に外部から働く力はないので、運動量保存より、
です。系に外部から働く力はないので、運動量保存より、 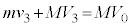 ∴
∴ 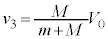 ......[答]
......[答]
ばねの長さが変化しなくなった後、系の運動エネルギーは、問6の結果を用いて、
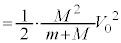 ・・・⑤
・・・⑤ばねの弾性エネルギーは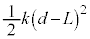 ・・・⑥
・・・⑥
瞬間的な力を加えた直後から、ばねの長さが変化しなくなるまでに、小物体Bが台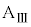 の上を滑った総距離を
の上を滑った総距離を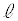 として、動摩擦力
として、動摩擦力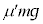 がした仕事は
がした仕事は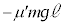 (負の仕事です)瞬間的な力を加えた直後から、ばねの長さが変化しなくなるまでのエネルギーの原理より、
(負の仕事です)瞬間的な力を加えた直後から、ばねの長さが変化しなくなるまでのエネルギーの原理より、 ∴ 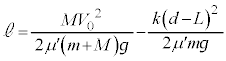 ......[答]
......[答]
問8 ばねの長さがDのとき、台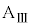 には、x軸負方向に動摩擦力
には、x軸負方向に動摩擦力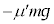 ,ばねの弾性力
,ばねの弾性力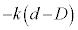 が働きます。台
が働きます。台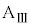 の加速度をAとして、台
の加速度をAとして、台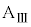 の運動方程式は、
の運動方程式は、 ∴ 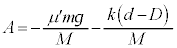 ・・・⑦
・・・⑦
台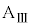 上で見て、小物体Bには、x軸正方向に動摩擦力
上で見て、小物体Bには、x軸正方向に動摩擦力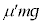 ,ばねの弾性力
,ばねの弾性力 ,x軸正方向に慣性力
,x軸正方向に慣性力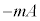 (>0,∵
(>0,∵ 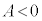 )が働きます。台
)が働きます。台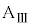 上で見た小物体Bの運動方程式は、
上で見た小物体Bの運動方程式は、 ⑦を代入して、
∴ 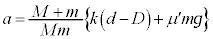 ......[答]
......[答]
問9 台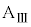 が速度
が速度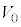 を得たときの系の力学的エネルギーは
を得たときの系の力学的エネルギーは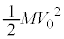 です。ばねの長さが
です。ばねの長さが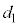 になったとき、ばねの弾性エネルギーは
になったとき、ばねの弾性エネルギーは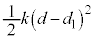 ,このとき小物体Bは台
,このとき小物体Bは台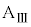 に対して静止するので、小物体Bと台
に対して静止するので、小物体Bと台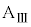 の速度は一致し問6の
の速度は一致し問6の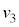 になり、このときの運動エネルギーは
になり、このときの運動エネルギーは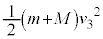 です。この間に動摩擦力のした仕事は
です。この間に動摩擦力のした仕事は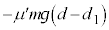 です。エネルギーの原理より、
です。エネルギーの原理より、 問6の結果を代入して、
∴ 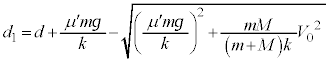 ......[答]
......[答] 注.上ではエネルギーを考えて解答しましたが、問8で加速度を求めているので、出題者の意図としては、加速度から求めさせたいのかも知れません。ある時刻におけるばねの長さDを変位と考えると、問8の結果は単振動を表しており、単振動の公式: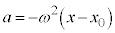 と問8の結果より、単振動の角振動数は
と問8の結果より、単振動の角振動数は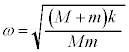 です。
です。 台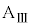 が速度
が速度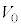 で動き出すと、小物体Bは台上で見て速度
で動き出すと、小物体Bは台上で見て速度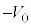 で動き出します。問8の結果より、振動中心は
で動き出します。問8の結果より、振動中心は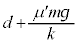 にあり、このときの小物体Bの位置は、振動中心から
にあり、このときの小物体Bの位置は、振動中心から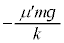 ずれた位置にあります。
ずれた位置にあります。
単振動の振幅をwとして、単振動の公式: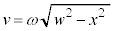 より、
より、 これより、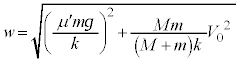 となり、1回目の折り返しの位置は、振動中心
となり、1回目の折り返しの位置は、振動中心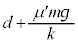 からwだけ縮んだ位置で、
からwだけ縮んだ位置で、 となります。
問10 いきなり運動を停止した後の状況を考えるのは難しいので、2回目の折り返し、3回目の折り返し、4回目の折り返しの状況を考えます。それぞれの場合のばねの長さを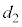 ,
,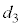 ,
,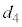 とします。動摩擦力により負の仕事を受けるので、
とします。動摩擦力により負の仕事を受けるので、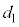 ,
,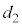 ,
,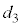 ,
,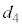 と次第に自然長dに近づいていきます。
と次第に自然長dに近づいていきます。 1回目、3回目の折り返しでは、ばねが縮んだところ(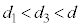 )から折り返して、x軸正方向に進んでいきます。動摩擦力はx軸負方向に働き、1回目から2回目、3回目から4回目までで動摩擦力は負の仕事
)から折り返して、x軸正方向に進んでいきます。動摩擦力はx軸負方向に働き、1回目から2回目、3回目から4回目までで動摩擦力は負の仕事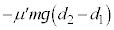 ,
,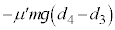 をします。2回目、4回目の折り返しでは、ばねが伸びたところ(
をします。2回目、4回目の折り返しでは、ばねが伸びたところ(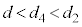 )から折り返して、x軸負方向に進んでいきます。動摩擦力はx軸正方向に働き、2回目から3回目までで動摩擦力は負の仕事
)から折り返して、x軸負方向に進んでいきます。動摩擦力はx軸正方向に働き、2回目から3回目までで動摩擦力は負の仕事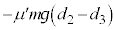 をします。
をします。
これより、jを自然数として、奇数回目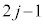 回目の折り返しから偶数回目
回目の折り返しから偶数回目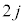 回目の折り返し、偶数回目
回目の折り返し、偶数回目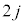 回目の折り返しから奇数回目
回目の折り返しから奇数回目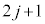 回目の折り返しを分けて考えることにします。
回目の折り返しを分けて考えることにします。
小物体Bが折り返すとき、小物体Bは台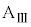 に対して静止するので、このとき、小物体Bと台
に対して静止するので、このとき、小物体Bと台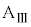 は問6の状況のように同じ速度
は問6の状況のように同じ速度 となり、各折り返し時点でのエネルギーは等しく、エネルギーの変化は弾性エネルギーの変化だけになります。
となり、各折り返し時点でのエネルギーは等しく、エネルギーの変化は弾性エネルギーの変化だけになります。
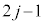 回目から
回目から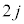 回目まででは、ばねは伸びるので
回目まででは、ばねは伸びるので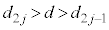 ,弾性エネルギーは
,弾性エネルギーは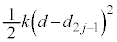 から
から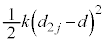 まで変化します。動摩擦力のする仕事は
まで変化します。動摩擦力のする仕事は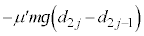 です。この間のエネルギーの原理より、
です。この間のエネルギーの原理より、 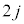 回目から
回目から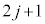 回目まででは、ばねは縮むので
回目まででは、ばねは縮むので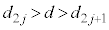 ,弾性エネルギーは
,弾性エネルギーは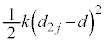 から
から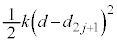 まで変化します。動摩擦力のする仕事は
まで変化します。動摩擦力のする仕事は です。この間のエネルギーの原理より、
です。この間のエネルギーの原理より、⑧を代入すると、
問9の結果を代入すると、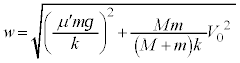 として、
として、 ⑧より、
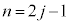 のとき、
のとき、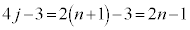
 のとき、
のとき、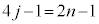
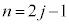 のとき
のとき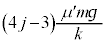 の符号はプラス、wの符号はマイナス、
の符号はプラス、wの符号はマイナス、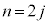 のとき
のとき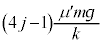 の符号はマイナス、wの符号はプラス、小物体Bが台
の符号はマイナス、wの符号はプラス、小物体Bが台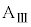 に対して運動を停止するのは、n回目の折り返しの位置(
に対して運動を停止するのは、n回目の折り返しの位置(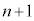 回目の折り返しはしない)において静止し、ばねの弾性力+慣性力が最大静止摩擦力を越えなくなったときなので、
回目の折り返しはしない)において静止し、ばねの弾性力+慣性力が最大静止摩擦力を越えなくなったときなので、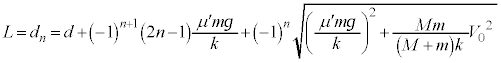 ......[答]
......[答]注.この問題も、東大19年[1]のように、振動中心と振幅を追っていけば、問9注.を利用して解答することができます。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。なお、解答は、
苦学楽学塾制作です。©2005-2025(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 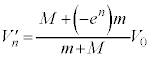 ......[答]
......[答]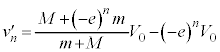
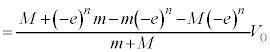
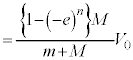 ......[答]
......[答]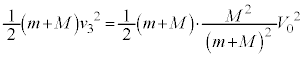
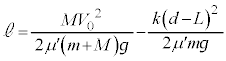 ......[答]
......[答]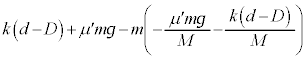
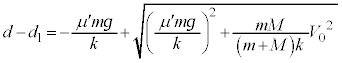
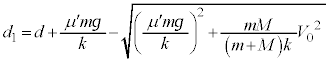 ......[答]
......[答]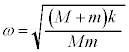 です。
です。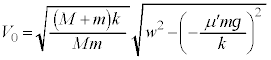
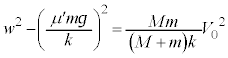
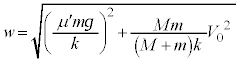 となり、1回目の折り返しの位置は、振動中心
となり、1回目の折り返しの位置は、振動中心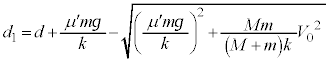
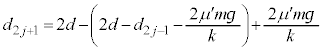
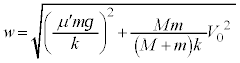 として、
として、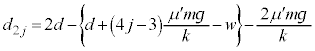
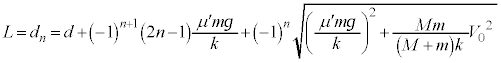 ......[答]
......[答]