微分法(最大最小・グラフ・速度加速度)演習問題
横国大工数学'09年後期[5]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
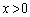 で定義された関数
で定義された関数
を考える。ただし、aは定数である。次の問いに答えよ。
(1) 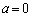 のとき、
のとき、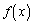 は増加関数であることを示せ。
は増加関数であることを示せ。 (2) 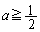 のとき、
のとき、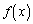 は減少関数であることを示せ。
は減少関数であることを示せ。 [解答へ]
北見工大数学'08年[5]
一般に、直線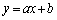 が関数
が関数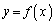 のグラフの漸近線であるとは、
のグラフの漸近線であるとは、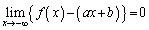 または
または 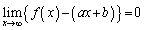 であることを言う。
であることを言う。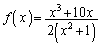 とするとき、以下の問いに答えよ。
とするとき、以下の問いに答えよ。
(1) 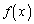 の増減を調べ、
の増減を調べ、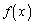 が極小になるxの値、
が極小になるxの値、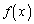 が極大になるxの値があればそれぞれすべて求めよ。
が極大になるxの値があればそれぞれすべて求めよ。 (2) 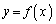 が下に凸になるxの範囲を求めよ。
が下に凸になるxの範囲を求めよ。 (3) 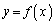 に変曲点があればすべて求め、それぞれの点における
に変曲点があればすべて求め、それぞれの点における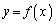 の接線の傾きを求めよ。
の接線の傾きを求めよ。 (4) 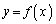 の漸近線をすべて求めよ。
の漸近線をすべて求めよ。 (5) 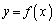 のグラフの概形を描け。また、(3)で求めた変曲点があればそれぞれの変曲点における接線を、(4)で求めた漸近線があれば漸近線を、
のグラフの概形を描け。また、(3)で求めた変曲点があればそれぞれの変曲点における接線を、(4)で求めた漸近線があれば漸近線を、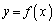 のグラフと同じxy平面上に描け。
のグラフと同じxy平面上に描け。 [解答へ]
阪大理系数学'08年前期[3]
Nを2以上の自然数とする。
(1) 関数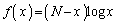 を
を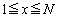 の範囲で考える。このとき、曲線
の範囲で考える。このとき、曲線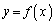 は上に凸であり、関数
は上に凸であり、関数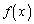 は極大値を1つだけとる。このことを示せ。
は極大値を1つだけとる。このことを示せ。 (2) 自然数の列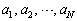 を
を 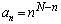 (
(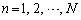 )
)で定める。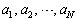 のうちで最大の値をMとし、
のうちで最大の値をMとし、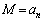 となるnの個数をkとする。このとき
となるnの個数をkとする。このとき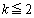 であることを示せ。
であることを示せ。 (3) (2)で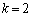 となるのは、Nが2のときだけであることを示せ。
となるのは、Nが2のときだけであることを示せ。 [解答へ]
東工大数学'09年後期[2]
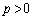 ,
,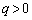 であるような点P
であるような点P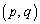 から双曲線
から双曲線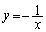 へ引いた2本の接線の接点をA,Bとする。
へ引いた2本の接線の接点をA,Bとする。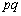 をtとおいて、三角形PABの面積をtの式として表せ。また、この面積の最小値を求めよ。
をtとおいて、三角形PABの面積をtの式として表せ。また、この面積の最小値を求めよ。
[解答へ]
東京理科大理数学'09年[2]
以下の(1)から(3)の問いに答えよ。ただし、(1)および(2)で得られた結論は、必要なら(3)の解答の際に用いてよい。
(1) 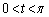 をみたす実数tをとる。実数θ が
をみたす実数tをとる。実数θ が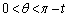 の範囲を動くとき、関数
の範囲を動くとき、関数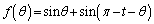 の値が最大になるようなθ の値と、関数
の値が最大になるようなθ の値と、関数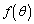 の最大値
の最大値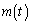 を求めよ。
を求めよ。 (2) (1)で求めた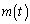 を用いて関数
を用いて関数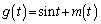 を定める。実数tが
を定める。実数tが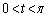 の範囲を動くとき、関数
の範囲を動くとき、関数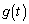 の値が最大になるようなtの値と、関数
の値が最大になるようなtの値と、関数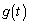 の最大値Mを求めよ。
の最大値Mを求めよ。 (3) 半径1の円Tに内接する三角形ABCの頂点Aにおける内角をtで表し、頂点Cにおける内角をθ で表すことにする。
(a) 頂点Aにおける内角tが動く範囲を求めよ。
(b) 頂点Aにおける内角tを一定に保ちながら頂点Aが円T上を動くとき、線分ABと線分ACの長さの和が最大になるための必要十分条件を三角形ABCについての条件として述べよ。
(c) (b)で求めた条件をみたす三角形ABCの頂点Aにおける内角tを、(a)で求めた範囲で動かすことにより、この三角形の3辺の長さの和の最大値を求めよ。
[解答へ]
大分大医数学'08年[2]
a,bは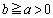 をみたす定数とする。x,yが
をみたす定数とする。x,yが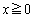 ,
,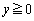 ,
,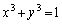 をみたしながら変化するとき、
をみたしながら変化するとき、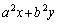 のとり得る値の範囲を求めよ。
のとり得る値の範囲を求めよ。
[解答へ]
富山大医学部数学'08年[2]
水平な平面αを考える。α上の点を中心とし半径1である球Sの、αより上にある部分をHとする。平行光線がαとHに斜め上からあたっていて、α上にHの影ができているとする。その平行光線とαとのなす角がθ (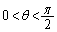 )であるとき、次の問いに答えよ。なお、半径1の球の表面積が
)であるとき、次の問いに答えよ。なお、半径1の球の表面積が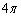 であることは用いてよい。
であることは用いてよい。
(1) Hの、光線があたっている部分の面積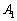 を求めよ。
を求めよ。
(2) α上にできる影の面積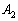 を求めよ。ただし、αとSとが交わってできる円の内部は影とは呼ばないこととする。
を求めよ。ただし、αとSとが交わってできる円の内部は影とは呼ばないこととする。
(3) 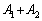 を最小にするようなθ を
を最小にするようなθ を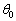 とするとき、
とするとき、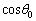 の値を求めよ。
の値を求めよ。
[解答へ]
東京学芸大数学'08年[4]
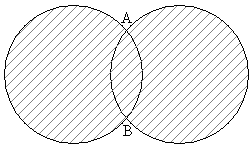 半径1の2つの円が図のように異なる2点で交わっている。2つの交点をA,Bとし、弧ABに対する円の中心角の大きさをθ (
半径1の2つの円が図のように異なる2点で交わっている。2つの交点をA,Bとし、弧ABに対する円の中心角の大きさをθ (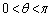 )とする。斜線をつけた図形をDとし、Dの周囲の長さをL,Dの面積をSとする。
)とする。斜線をつけた図形をDとし、Dの周囲の長さをL,Dの面積をSとする。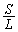 を最大にするθ がただ1つ存在することを示せ。
を最大にするθ がただ1つ存在することを示せ。
[解答へ]
東工大数学'96年前期[4]
関数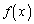 は微分可能で次の(イ),(ロ),(ハ)をみたすものとする。
は微分可能で次の(イ),(ロ),(ハ)をみたすものとする。
(イ) 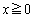 のとき
のとき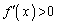
(ロ) 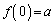 (ただし、
(ただし、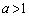 )
) (ハ) 曲線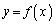 上の点P
上の点P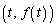 (
(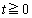 )における接線とx軸との交点をQ,法線とx軸との交点をRとしたとき、線分QRの長さ
)における接線とx軸との交点をQ,法線とx軸との交点をRとしたとき、線分QRの長さ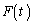 は関係式
は関係式 をみたす。
このとき次の問いに答えよ。
(1) 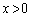 で
で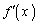 は単調増加で、
は単調増加で、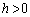 に対し
に対し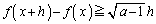 をみたすことを示せ。
をみたすことを示せ。 (2) 点Pが曲線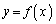 (
(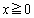 )上を動くとき
)上を動くとき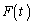 の最小値を求めよ。
の最小値を求めよ。 [解答へ]
鹿児島大理系数学'08年[3]
eを自然体数の底とする。このとき、次の各問いに答えよ。
(1) 積分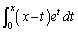 を計算することにより、次の等式を証明せよ。
を計算することにより、次の等式を証明せよ。 (2) すべての自然数nについて、等式
が成り立つことを数学的帰納法により証明せよ。
(3) 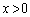 のとき、すべての自然数nについて、次の不等式が成り立つことを証明せよ。
のとき、すべての自然数nについて、次の不等式が成り立つことを証明せよ。 [解答へ]
九大理系数学'09年前期[5]
曲線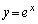 上を動く点Pの時刻tにおける座標を
上を動く点Pの時刻tにおける座標を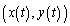 と表し、Pの速度ベクトルと加速度ベクトルをそれぞれ
と表し、Pの速度ベクトルと加速度ベクトルをそれぞれ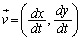 と
と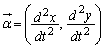 とする。すべての時刻tで
とする。すべての時刻tで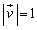 かつ
かつ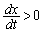 であるとして、次の問いに答えよ。
であるとして、次の問いに答えよ。
(1) Pが点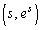 を通過する時刻における速度ベクトル
を通過する時刻における速度ベクトル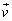 をsを用いて表せ。
をsを用いて表せ。 (2) Pが点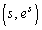 を通過する時刻における加速度ベクトル
を通過する時刻における加速度ベクトル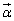 をsを用いて表せ。
をsを用いて表せ。 (3) Pが曲線全体を動くとき、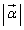 の最大値を求めよ。
の最大値を求めよ。 [解答へ]
静岡大理数学'10年[2]
次の問いに答えよ。
(1) 不等式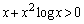 が成り立つことを示せ。
が成り立つことを示せ。 (2) 関数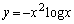 の増減、グラフの凹凸を調べ、グラフの概形をかけ。
の増減、グラフの凹凸を調べ、グラフの概形をかけ。 [解答へ]
北大数学'10年前期[4]
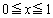 に対して
に対して
と定める。ただし、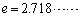 は自然対数の底である。
は自然対数の底である。
(1) 不定積分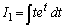 ,
,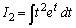 を求めよ。
を求めよ。 (2) 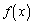 をxの指数関数と多項式を用いて表せ。
をxの指数関数と多項式を用いて表せ。 (3) 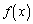 は
は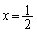 で極大となることを示せ。
で極大となることを示せ。 [解答へ]
名工大数学'10年前期[4]
関数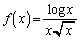 (
(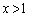 )に対して次の問いに答えよ。必要ならば、自然対数の底eの値は
)に対して次の問いに答えよ。必要ならば、自然対数の底eの値は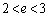 であることを用いてよい。
であることを用いてよい。
(1) 関数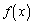 の増減を調べよ。
の増減を調べよ。 (2) 曲線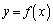 上の点P
上の点P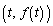 における法線
における法線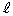 の方程式を求めよ。
の方程式を求めよ。 (3) 点Pからx軸に下ろした垂線をPQとする。(2)で求めた法線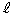 とx軸との交点をRとする。2点Q,Rの距離の最大値を求めよ。
とx軸との交点をRとする。2点Q,Rの距離の最大値を求めよ。 [解答へ]
旭川医大数学'10年[3]
関数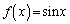 (
(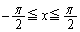 )の逆関数を
)の逆関数を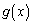 (
(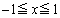 )とおくとき、次の問いに答えよ。
)とおくとき、次の問いに答えよ。
問1 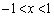 のとき、
のとき、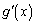 をxを用いて表せ。
をxを用いて表せ。 問2 曲線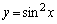 (
(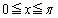 )と直線
)と直線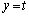 (
(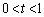 )の2つの交点のx座標を、それぞれα,β (
)の2つの交点のx座標を、それぞれα,β (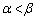 )とおくとき、
)とおくとき、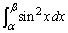 をt と関数gを用いて表せ。
をt と関数gを用いて表せ。 問3 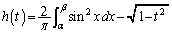 (
(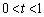 )とおくとき、
)とおくとき、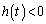 (
(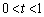 )を示し、
)を示し、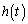 を最小にするt の値を求めよ。
を最小にするt の値を求めよ。 [解答へ]
京都工繊大数学'10年[4]
(1) 不定積分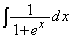 を求めよ。
を求めよ。 (2) 実数aに対して定積分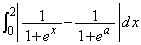 の値を
の値を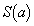 とおく。aが
とおく。aが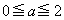 の範囲を動くとき、
の範囲を動くとき、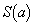 の最小値を求めよ。
の最小値を求めよ。 [解答へ]
大阪市大数学'11年[3]
p,qは正の実数で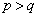 とする。
とする。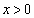 において、2つの関数
において、2つの関数
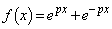 ,
,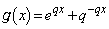
問1 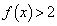 を示せ。
を示せ。 問2 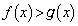 を示せ。
を示せ。 問3 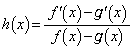 とするとき、
とするとき、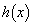 は
は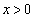 において単調減少であることを示せ。
において単調減少であることを示せ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 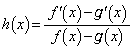 とするとき、
とするとき、