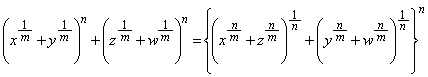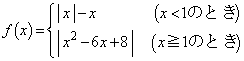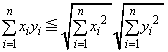�_�E���w�I�A�[�@���K���
���s��o�ϐ��w'08�N[4]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���̐�x�ɑ��āA�O�ӂ̒�����
�ŗ^������O�p�`ABC���l����B���̖₢�ɓ�����B
(1) 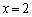 �̂Ƃ��A�O�p�`ABC�����݂���悤��k�̒l�͈̔͂����߂�B
�̂Ƃ��A�O�p�`ABC�����݂���悤��k�̒l�͈̔͂����߂�B (2) �C�ӂ̐��̐�t�ɑ��ĕs����
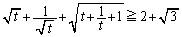 �@����@
�@����@�����
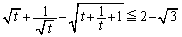 �@����A
�@����A���������邱�Ƃ������B�������A�A���ؖ�����ۂɇ@�𗘗p���Ă悢�B
(3) (2)�̌��ʂ𗘗p���āA�C�ӂ̐��̐�x�ɑ��ĎO�p�`ABC�����݂���悤��k�̒l�͈̔͂����߂�B
[��]
�����㐔�w'09�N[4]
���ׂĂ̐��̎���x�ɑ��Ē�`���ꂽ�A����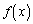 �͎���(a)�C(b)�������̂Ƃ���B
�͎���(a)�C(b)�������̂Ƃ���B
(a) ���ׂĂ̐��̎���x�Cy�ɑ���
(b) ���ׂĂ̎��R��n�ɑ���
���̊�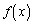 �ɂ��āA���̖₢�ɓ�����B
�ɂ��āA���̖₢�ɓ�����B
(1) x�𐳂̎����Ƃ���Ƃ��A���̒l�����߂�B
(2) a��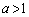 �����L�����Ƃ���Ƃ��A���̕s�������ؖ�����B
�����L�����Ƃ���Ƃ��A���̕s�������ؖ�����B (3) a�Cb��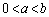 �����L�����Ƃ���Ƃ��A���̕s�������ؖ�����B
�����L�����Ƃ���Ƃ��A���̕s�������ؖ�����B (4) a�Cb��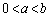 ���������ł�(3)�̕s���������藧���Ƃ�p���āA���̎���x�Cy�ɑ��āA���̕s�������ؖ�����B
���������ł�(3)�̕s���������藧���Ƃ�p���āA���̎���x�Cy�ɑ��āA���̕s�������ؖ�����B [��]
���嗝�n���w'99�N�O��[5]
�ȉ��̖₢�ɓ�����B�������A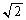 �C
�C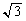 �C
�C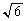 ���������ł��邱�Ƃ͎g���Ă悢�B
���������ł��邱�Ƃ͎g���Ă悢�B
(1) �L����p�Cq�Cr�ɂ��āA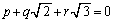 �Ȃ�A
�Ȃ�A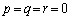 �ł��邱�Ƃ������B
�ł��邱�Ƃ������B (2) �����W����2����
�ɂ��āA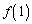 �C
�C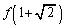 �C
�C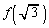 �̂����ꂩ�͖������ł��邱�Ƃ������B
�̂����ꂩ�͖������ł��邱�Ƃ������B [��]
�É��嗝�n���w'09�N[1]
���̖₢�ɓ�����B
(1) ���ׂĂ̎��R��n�ɑ��āA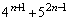 ��21�Ŋ����邱�Ƃ��ؖ�����B
��21�Ŋ����邱�Ƃ��ؖ�����B (2) ���̏��������萔�łȂ�������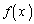 �𐄒肵�A���̐��肪���������Ƃ��ؖ�����B
�𐄒肵�A���̐��肪���������Ƃ��ؖ�����B (a) 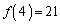
(b) ���ׂĂ̎��R��n�ɑ��āA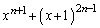 ��
��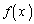 �Ŋ�����B
�Ŋ�����B [��]
�ޗnj�����吔�w'09�N[2]
n��2�ȏ�̐����Ƃ��A1����n�܂ł̑��قȂ�n�̐����������ɕ��ׂē�����e����σ�ɑ��āA������i�Ԗڂ̐�����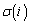 �ƋL���B���̂Ƃ��A����
�ƋL���B���̂Ƃ��A����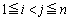 �C����
�C����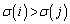 ���������̑�
���������̑�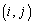 �̌���
�̌���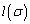 �Ƃ����B�����1����n�܂ł̏���σ�S�̂̂Ȃ��W����S�Ƃ���B����σ��S�S�̂��Ƃ��A
�Ƃ����B�����1����n�܂ł̏���σ�S�̂̂Ȃ��W����S�Ƃ���B����σ��S�S�̂��Ƃ��A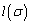 �̑��a
�̑��a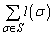 �����߂�B
�����߂�B
[��]
���H�吔�w'90�N�O��[1]
x�Cy�Cz�Cw�𐳐��Ƃ���B�C�ӂ̐��̐���m�Cn�ɑ��āA
�����藧���߂̕K�v�\�����������߂�B
[��]
���㎕�吔�w'09�N[1]
���W���ʂ܂��͍��W��Ԃɂ����āA���W���������ׂĐ����ł���_���i�q�_�Ƃ����B�ȉ��̊e�₢�ɓ�����B
(1) 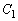 �����W���ʏ�̔��a
�����W���ʏ�̔��a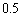 �̉~�Ƃ���B
�̉~�Ƃ���B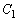 �������Ɋi�q�_���܂܂Ȃ��Ƃ��A
�������Ɋi�q�_���܂܂Ȃ��Ƃ��A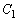 �̒��S
�̒��S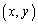 �����݂�����̈��
�����݂�����̈��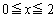 �C
�C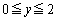 �͈̔͂Ő}������B
�͈̔͂Ő}������B (2) 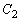 �����W���ʏ�̔��a
�����W���ʏ�̔��a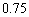 �̉~�Ƃ���B
�̉~�Ƃ���B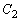 �͒��S���ǂ̂悤�Ȉʒu�Ɉړ������Ă��K�������Ɋi�q�_���܂ނ��Ƃ��ؖ�����B
�͒��S���ǂ̂悤�Ȉʒu�Ɉړ������Ă��K�������Ɋi�q�_���܂ނ��Ƃ��ؖ�����B (3) S�����W��ԓ��̔��ar�̋��Ƃ���BS�͔��a��ω��������ɒ��S���ǂ̂悤�Ȉʒu�Ɉړ������Ă��A�K�������Ɋi�q�_���܂ނ��̂Ƃ���B���̂Ƃ�r�̂Ƃ肤��l�͈̔͂����߂�B������S�̓����Ƃ́AS�̒��S����̋�����r��菬�����_�S�̂���Ȃ�W���̂��Ƃł���B
[��]
��嗝�n���w'09�N���[2]
�ȉ��̖₢�ɓ�����B
(1) 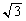 ���������ł��邱�Ƃ��ؖ�����B
���������ł��邱�Ƃ��ؖ�����B (2) a�Cb��L�����Ƃ���B������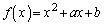 ��
��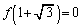 �����Ƃ��Aa�Cb�����߂�B
�����Ƃ��Aa�Cb�����߂�B (3) n��2�ȏ�̎��R���Ƃ���B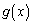 �͗L�������W���Ƃ���n���������ōō����̌W����1�ł���Ƃ���B
�͗L�������W���Ƃ���n���������ōō����̌W����1�ł���Ƃ���B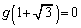 �ƂȂ�Ƃ��A
�ƂȂ�Ƃ��A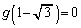 �������B
�������B [��]
�ޗnj�����吔�w'09�N[1]
xyz��Ԃɂ����Č��_O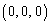 �𒆐S�Ƃ��锼�a1�̋��ʂ�S�Ƃ��A����S����_N
�𒆐S�Ƃ��锼�a1�̋��ʂ�S�Ƃ��A����S����_N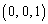 �������������ɑ�����_P
�������������ɑ�����_P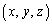 �ɑ��āA2�_N�CP��ʂ钼����xy����
�ɑ��āA2�_N�CP��ʂ钼����xy����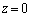 �Ƃ̌�_��Q�Ƃ����B
�Ƃ̌�_��Q�Ƃ����B
(1) �_Q�̍��W�����߂�B
(2) ����S��̔C�ӂ̓_R�ɑ���R�̂ǂ�ȋ߂��ɂ��AS��̓_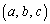 �Ŋe���Wa�Cb�Cc�����ׂėL��������Ȃ���̂����݂��邱�Ƃ��ؖ�����B
�Ŋe���Wa�Cb�Cc�����ׂėL��������Ȃ���̂����݂��邱�Ƃ��ؖ�����B [��]
�É��嗝���w'08�N���[5]
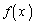 �͋��
�͋��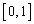 �Œ�`���ꂽ�A�����ł���A
�Œ�`���ꂽ�A�����ł���A
�����Ƃ���B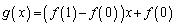 (
(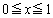 )�Ƃ���B���̖₢�ɓ�����B
)�Ƃ���B���̖₢�ɓ�����B
(1) 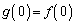 �C
�C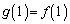 �����
����� �����藧���Ƃ������A�����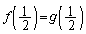 �ł��邱�Ƃ������B
�ł��邱�Ƃ������B (2) n�����R���Ƃ��A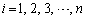 �ɑ��āA
�ɑ��āA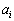 ��0�܂���1�Ƃ���B���̓������ؖ�����B
��0�܂���1�Ƃ���B���̓������ؖ�����B (3) 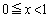 �ɑ���
�ɑ��� �Ƃ���B�������A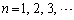 �ɑ��āA
�ɑ��āA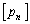 ��
��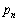 ���z���Ȃ��ő�̐�����\���B���̂Ƃ��A
���z���Ȃ��ő�̐�����\���B���̂Ƃ��A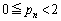 (
(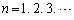 )�����
)����� �ł��邱�Ƃ������B
(4) 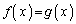 (
(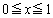 )�ł��邱�Ƃ������B
)�ł��邱�Ƃ������B [��]
�D�y��吔�w'10�N[4]
����n�ɑ��āA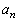 �������Œ�`����B
�������Œ�`����B
(1) 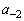 �C
�C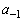 �����߂�B
�����߂�B (2) 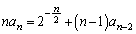 �����藧���Ƃ������B
�����藧���Ƃ������B (3) 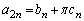 (������
(������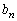 �C
�C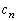 �͗L����)�ƕ\����邱�Ƃ������B�܂�
�͗L����)�ƕ\����邱�Ƃ������B�܂�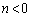 �̂Ƃ���
�̂Ƃ���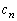 �����߂�B�K�v�Ȃ��π���������ł��邱�Ƃ�p���Ă悢�B
�����߂�B�K�v�Ȃ��π���������ł��邱�Ƃ�p���Ă悢�B [��]
���㎕�吔�w'10�N[1]
a�Cb�Cc�𑊈قȂ鐳�̎����Ƃ���Ƃ��A�ȉ��̊e�₢�ɓ�����B
(1) ����2���̑召���r����B
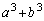 �C
�C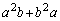
(2) ����4���̑召���r���A�����������珇�ɕ��ׂ�B
(3) x�Cy�Cz�𐳂̎����Ƃ���Ƃ��A
�̂Ƃ肤��l�͈̔͂����߂�B
[��]
���吔�w'10�N[4]
xy���ʏ��x���W��y���W���Ƃ��ɐ����ł���_���i�q�_�ƌĂԁB
(1) 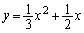 �̃O���t��ɖ����̊i�q�_�����݂��邱�Ƃ������B
�̃O���t��ɖ����̊i�q�_�����݂��邱�Ƃ������B (2) a�Cb�͎�����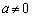 �Ƃ���B
�Ƃ���B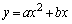 �̃O���t��ɁA�_
�̃O���t��ɁA�_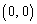 �ȊO�Ɋi�q�_��2���݂���A�������݂��邱�Ƃ������B
�ȊO�Ɋi�q�_��2���݂���A�������݂��邱�Ƃ������B [��]
���k�嗝�n���w'10�N���[1]
n��2�ȏ�̎��R���Ƃ���B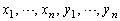 ��
��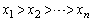 �C
�C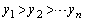 ���������Ƃ���B
���������Ƃ���B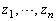 ��
��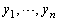 ��C�ӂɕ��בւ������̂Ƃ���Ƃ��A
��C�ӂɕ��בւ������̂Ƃ���Ƃ��A
�����藧���Ƃ������B�܂��A���������藧�̂͂ǂ̂悤�ȂƂ���������B
[��]
��t�吔�w'10�N[11]
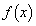 �͎����S�̂Œ�`���ꂽ���Ƃ���B����a�Ɋւ������(P)���l����B
�͎����S�̂Œ�`���ꂽ���Ƃ���B����a�Ɋւ������(P)���l����B
(P) ���̎���r���\���������I�ׂA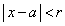 ���݂������ׂĂ̎���x�ɑ���
���݂������ׂĂ̎���x�ɑ���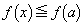 �����藧�B
�����藧�B ���̂Ƃ��A�ȉ��̖₢�ɓ�����B
(1) ����a������(P)���݂����A���A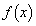 ��
��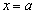 �Ŕ����\�Ȃ�A
�Ŕ����\�Ȃ�A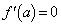 �ł��邱�Ƃ��ؖ�����B
�ł��邱�Ƃ��ؖ�����B (2) ��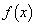 ��
�� �Œ�`����Ă���Ƃ��A����(P)���݂����悤�Ȏ���a�S�̂̏W�������肹��B
(3) ��ʂɁA�����S�̂Œ�`���ꂽ��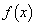 �ɑ��A���̖���͐��������B��������Ώؖ����A�������Ȃ���Δ����������B
�ɑ��A���̖���͐��������B��������Ώؖ����A�������Ȃ���Δ����������B (����) ���ׂĂ̎���a������(P)���݂����Ȃ�A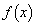 �͒萔���ł���B
�͒萔���ł���B [��]
��嗝�n���w'11�N�O��[4]
a�Cb�Cc�𐳂̒萔�Ƃ��Ax�̊�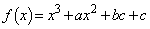 ���l����B�ȉ��A�萔�͂��ׂĎ����Ƃ���B
���l����B�ȉ��A�萔�͂��ׂĎ����Ƃ���B
(1) �萔p�Cq�ɑ��A�����݂����萔r�����݂��邱�Ƃ������B
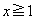 �Ȃ��
�Ȃ�� 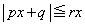
(2) �P����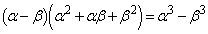 ��p���āA�����݂����萔k�Cl�����݂��邱�Ƃ������B
��p���āA�����݂����萔k�Cl�����݂��邱�Ƃ������B 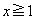 �Ȃ��
�Ȃ�� 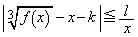
(3) ���ׂĂ̎��R��n�ɑ��āA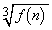 �����R���ł���Ƃ���B���̂Ƃ���
�����R���ł���Ƃ���B���̂Ƃ���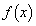 �́A���R���̒萔m��p����
�́A���R���̒萔m��p����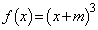 �ƕ\����邱�Ƃ������B
�ƕ\����邱�Ƃ������B [��]
�啪��㐔�w'11�N[1]
����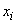 �C
�C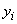 �C
�C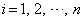 �ɑ��Ď��̕s�������ؖ�����B�������An�͎��R���ł���B
�ɑ��Ď��̕s�������ؖ�����B�������An�͎��R���ł���B
[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B