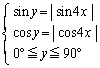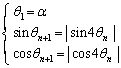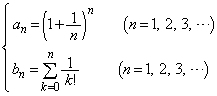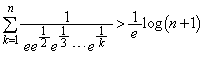数列演習問題
名大理系数学'08年前期[4A]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
次の問に答えよ。
(1) 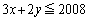 を満たす0以上の整数の組
を満たす0以上の整数の組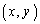 の個数を求めよ。
の個数を求めよ。 (2) 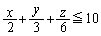 を満たす0以上の整数の組
を満たす0以上の整数の組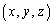 の個数を求めよ。
の個数を求めよ。 [解答へ]
広島大理系数学'08年前期[3]
2点A,Bと、その上を動く1個の石がある。この石は、時刻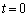 では点Aにあり、その後、次の規則(a),(b)にしたがって動く。
では点Aにあり、その後、次の規則(a),(b)にしたがって動く。
各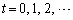 に対して、
に対して、
(a) 時刻tに石が点Aにあれば、時刻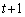 に石が点Aにある確率はc,点Bにある確率は
に石が点Aにある確率はc,点Bにある確率は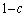 である。
である。 (b) 時刻tに石が点Bにあれば、時刻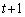 に石が点Bにある確率は2c,点Aにある確率は
に石が点Bにある確率は2c,点Aにある確率は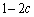 である。
である。 ただし、cは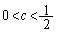 を満たす定数とする。
を満たす定数とする。
いま、nを自然数とし、時刻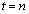 において石が点Aにある確率を
において石が点Aにある確率を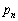 とするとき、次の問いに答えよ。
とするとき、次の問いに答えよ。
(1) 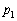 ,
,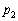 を求めよ。
を求めよ。 (2) 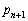 を
を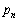 とcを用いて表せ。
とcを用いて表せ。 (3) 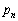 を求めよ。
を求めよ。 (4) 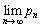 を求めよ。
を求めよ。 [解答へ]
高知大数学'08年[3]
数列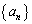 が
が
をみたすとき、次の問いに答えよ。
(1) xの2次式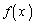 で、
で、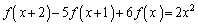 をみたすものを求めよ。
をみたすものを求めよ。 (2) 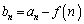 とおくとき、数列
とおくとき、数列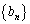 の一般項を求めよ。
の一般項を求めよ。 (3) 数列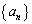 の一般項を求めよ。
の一般項を求めよ。 (4) 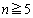 のとき、
のとき、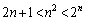 を数学的帰納法で示せ。
を数学的帰納法で示せ。 (5) 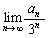 を求めよ。
を求めよ。 [解答へ]
東北大理系数学'08年後期[4]
(分数タイプ漸化式) 数列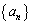 を
を
で定める。このとき、以下の問いに答えよ。
(1) 2つの実数αとβ に対して、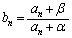 (
(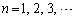 )とおく。
)とおく。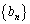 が等比数列となるようなαとβ (
が等比数列となるようなαとβ (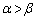 )を1組求めよ。
)を1組求めよ。 (2) 数列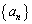 の一般項
の一般項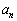 を求めよ。
を求めよ。 [解答へ]
豊橋技科大数学'09年[1]
二つの数列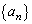 ,
,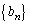 が次のように定義されている。
が次のように定義されている。
以下の問いに答えよ。
(1) 数列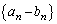 の一般項を求めよ。
の一般項を求めよ。 (2) 数列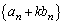 が等比数列となるとき、kの値を求めよ。ただし、
が等比数列となるとき、kの値を求めよ。ただし、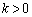 とする。
とする。 (3) 問(2)で求めたkの値を用いて、数列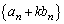 の一般項を求めよ。
の一般項を求めよ。 (4) 問(1),(3)の結果を用いて、数列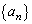 および
および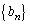 の一般項を求めよ。
の一般項を求めよ。 [解答へ]
信州大理医数学'09年[2]
数列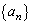 ,
,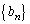 は
は
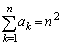 ,
,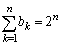
(1) 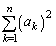
(2) 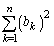
(3) 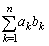
[解答へ]
信州大工数学'09年[2]
数列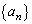 において
において
とおく。
 (
(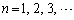 )
)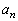 を求めよ。
を求めよ。
[解答へ]
金沢大理工数学'08年後期[4]
関数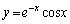 のグラフ上の点
のグラフ上の点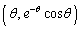 における接線のy切片を
における接線のy切片を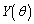 とする。次の問いに答えよ。
とする。次の問いに答えよ。
(1) 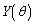 を求めよ。
を求めよ。 (2) 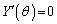 を満たす正の数θ を小さい順に
を満たす正の数θ を小さい順に とする。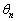 を求めよ。
を求めよ。 (3) 無限級数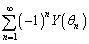 の和を求めよ。ただし、
の和を求めよ。ただし、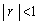 のとき
のとき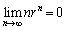 が成り立つことを用いてもよい。
が成り立つことを用いてもよい。 [解答へ]
東大文系数学'98年前期[3]
(1) xは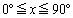 をみたす角とする。
をみたす角とする。 となるyをxで表し、そのグラフをxy平面上に図示せよ。
(2) αは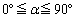 をみたす角とする。
をみたす角とする。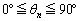 をみたす角
をみたす角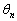 ,
,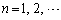 を
を
で定める。kを2以上の整数として、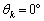 となるαの個数をkで表せ。
となるαの個数をkで表せ。 [解答へ]
愛媛大理系数学'10年[3]
2つの数列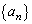 ,
,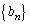 は、すべての自然数nについて
は、すべての自然数nについて
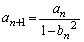 ,
, 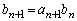
(1) 初項が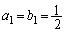 であるとする。
であるとする。 (ii) 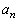 ,
,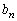 を表すnの式を推定し、それらの推定が正しいことを数学的帰納法によって証明せよ。
を表すnの式を推定し、それらの推定が正しいことを数学的帰納法によって証明せよ。 (2) 初項が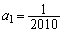 ,
,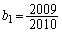 であるとする。
であるとする。 (ii) 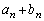 を求めよ。
を求めよ。 [解答へ]
兵庫県立大数学'10年[3]
数直線上の原点に点Aがある。点Aは次の規則に従って数直線上を正の向きに動いていく。
「Aが座標kの位置にあるとき数直線上の正の向きに1進む確率が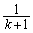 ,正の向きに2進む確率が
,正の向きに2進む確率が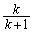 である。」
である。」 点Aが座標nの位置に立ち寄る確率を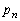 とする。このとき、次の問いに答えよ。
とする。このとき、次の問いに答えよ。
(1) 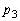 を求めよ。
を求めよ。 (2) 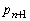 を
を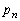 で表せ。
で表せ。 (3) 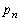 を求めよ。
を求めよ。 [解答へ]
新潟大数学'10年[2]
次の条件(ア)〜(ウ)を満たす数列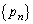 について考える。
について考える。
(ア) 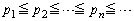 である。
である。 (イ) 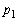 ,
,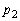 ,・・・,
,・・・,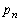 ,・・・ はどれも自然数である。
,・・・ はどれも自然数である。 (ウ) 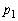 ,
,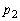 ,・・・,
,・・・,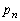 ,・・・ の中にはすべての自然数kが現れ、その個数はk以上
,・・・ の中にはすべての自然数kが現れ、その個数はk以上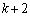 以下である。
以下である。 条件(ア)〜(ウ)を満たし、すべての自然数kがちょうどk個現れる数列
を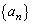 とする。このとき、次の問いに答えよ。
とする。このとき、次の問いに答えよ。
(1) 項数5の数列で、数列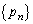 の初めの5項となり得るものをすべて挙げよ。
の初めの5項となり得るものをすべて挙げよ。 (2) 数列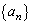 の第210項
の第210項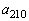 の値を求めよ。
の値を求めよ。 (3) 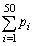 のとり得る最小の値を求めよ。
のとり得る最小の値を求めよ。 [解答へ]
横浜国大工数学'10年後期[5]
2つの数列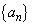 ,
,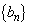 を
を
で定める。次の問いに答えよ。
(1) 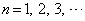 に対して、
に対して、 を示せ。
(2) 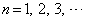 に対して、
に対して、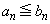 を示せ。
を示せ。 (3) nを2以上の自然数とする。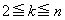 である自然数kに対して、
である自然数kに対して、 を示せ。
(4) 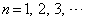 に対して、
に対して、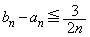 を示せ。ただし、
を示せ。ただし、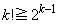 (
(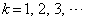 ) を証明なしに用いてよい。
) を証明なしに用いてよい。 [解答へ]
金沢大理系数学'11年[4]
次の問いに答えよ。
(1) 自然数nに対して、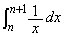 を求めよ。また
を求めよ。また を示せ。
(2) 2以上の自然数nに対して
を示せ。
(3) 2以上の自然数nに対して
を示せ。
[解答へ]
九大数学'11年前期[3]
数列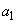 ,
,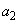 ,・・・,
,・・・,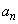 ,・・・ は
,・・・ は
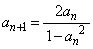 ,
, 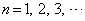
(1) 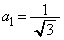 とするとき、一般項
とするとき、一般項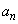 を求めよ。
を求めよ。 (2) 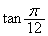 の値を求めよ。
の値を求めよ。 (3) 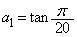 とするとき、
とするとき、 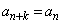 ,
, 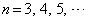
をみたす最小の自然数kを求めよ。
[解答へ]
阪大理系数学'11年前期[5]
正数rに対して、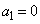 ,
,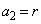 とおき、数列
とおき、数列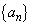 を次の漸化式で定める。
を次の漸化式で定める。
ただし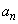 と
と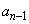 から漸化式を用いて
から漸化式を用いて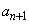 を決める際には硬貨を投げ、表が出たとき
を決める際には硬貨を投げ、表が出たとき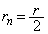 ,裏が出たとき
,裏が出たとき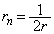 とする。ここで表が出る確率と裏が出る確率は等しいとする。
とする。ここで表が出る確率と裏が出る確率は等しいとする。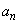 の期待値を
の期待値を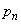 とするとき、以下の問いに答えよ。
とするとき、以下の問いに答えよ。
(1) 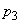 および
および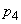 を、rを用いて表せ。
を、rを用いて表せ。 (2) 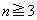 のときに
のときに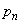 を、nとrを用いて表せ。
を、nとrを用いて表せ。 (3) 数列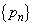 が収束するような正数rの範囲を求めよ。
が収束するような正数rの範囲を求めよ。 (4) rが(3)で求めた範囲を動くとき、極限値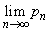 の最小値を求めよ。
の最小値を求めよ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。