波動分野
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
波動分野の目次のページです。
各項目の内容を作成するに従って、リンクを貼り付けていきます。
各項目の文字列をクリックすると、解説ページに飛びます。
(1) 波動現象 空間内の一点で起きた変化が、周囲に伝わる現象を波動と言います。波動の基礎事項を学びます。 (2) 波の公式 波の波長λ，振動数f として、波の進む速さvは、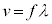
(3) 正弦波の式 波の波長λ，周期：T，振幅A，初期位相δとして、位置x，時刻tにおける波の変位yは、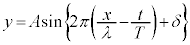
(4) 波の位相 正弦波の式の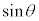
のθを、波動では角ではないので、位相と言います。 (5) 重ね合わせの原理 2つの波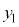
，
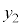の合成波は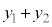
となります。これを重ね合わせの原理と言います。 (6) 波の干渉 2つの波を重ね合わせると、強め合うところと弱め合うところができます。これが波の干渉です。 (7) ホイヘンスの原理 ホイヘンスが光の波動説を説明するために提唱した波の伝播に関する原理です。 (8) 波の反射 波が境界面に達すると、自由端あるいは固定端として反射します。この違いを学びます。 (9) 定常波 同一振幅、同一波長、同一振動数で逆方向に進む2波が重ね合わされると、定常波が生じます。 (10) 波の回折 波が狭い間隙を通過するときの状況(波長と間隙の幅によって影響を受けます)を学びます。 (12) 弦の振動 弦を伝わる波は、基本振動の整数倍の振動に限られます。 (13) 管の振動 管(気柱)から発生する波は、基本振動の奇数倍の振動に限られます。 (14) うなり 微妙に異なる2つの振動数の波を重ね合わせるとうなりを生じます。 (15) ドップラー効果 音源と観測者が互いに近づいたり遠ざかったりすると、音源の振動数と異なる振動数の音が観測されます。これをドップラー効果を言います。 (16) 光波 光は波動か粒子かという対立がありましたが、光電効果により、両方の側面を持つ、ということになりました。 (17) 光の屈折 光波は境界面で屈折率の違いにより進行方向が変わり、屈折します。 (18) レンズ 凸レンズ、凹レンズの公式を導きます。 (19) 光の干渉 経路差と波長の関係に基づいて、2光が干渉する条件を考えます。 (20) 二重スリット 19世紀のはじめ、ヤングが黒く塗ったガラスに近接させて2本の傷をつけ、そこを通る光を干渉させて光の波長を求めた実験について考えます、この実験により、光の波動説が優勢になりました。 (21) 回折格子 二重スリットでは干渉はぼやけてしまうので、スリットの数を増やしたものを回折格子と言います。回折格子による干渉を考察します。 (22) 薄膜の干渉 ガラス面に薄膜を作ると、薄膜の上面・仮面で反射した光が干渉するために、色づいて見えます。 (23) ニュートン・リング 球面の一部と平面でできているレンズに光を当てて上から覗くと、円形の干渉縞が見えます。 (24) 単スリット スリットが一つだけでも、スリットのどこを通ったかにより光の干渉が起こります。 (25) 多重スリット 回折格子がどうして必要になるかを数式的に調べます。 (26) 光の分散 プリズムに光を通して壁に映すと虹が見えます。これは、屈折率が波長依存性をもつためです。 (27) 偏光 光波の横波の振動面は2方向あるため、偏光という現象が起きます。 (28) 波動方程式 発展的内容です。波動方程式の導出は形を変えて入試問題のネタとして使われています。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理基礎事項TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。