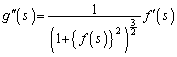積分法(面積・体積・曲線の長さ)演習問題
埼玉大理数学'09年[3]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
xy平面において2つの曲線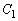 :
: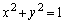 ,
,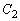 :
: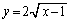 (
(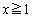 )を考える。次に、
)を考える。次に、 の点
の点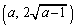 における接線を
における接線を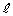 とする。ただし、
とする。ただし、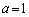 のとき、接線
のとき、接線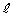 は直線
は直線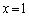 とする。
とする。
(1) 接線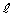 と円
と円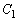 が共有点をもつようなaの範囲を求めよ。
が共有点をもつようなaの範囲を求めよ。 (2) aが(1)で求めた範囲にあるとき、接線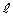 と円
と円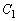 の共有点をP,Qとする。ただし、共有点が1点の場合は
の共有点をP,Qとする。ただし、共有点が1点の場合は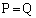 とする。このとき、線分PQの中点Mの軌跡Cの方程式を求めよ。
とする。このとき、線分PQの中点Mの軌跡Cの方程式を求めよ。 (3) 軌跡Cと円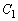 に囲まれ、点
に囲まれ、点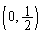 を含む図形の面積を求めよ。
を含む図形の面積を求めよ。 [解答へ]
九大理系数学'09年[3]
曲線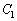 :
: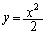 の点P
の点P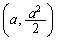 における法線と点Q
における法線と点Q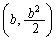 における法線の交点をRとする。ただし、
における法線の交点をRとする。ただし、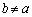 とする。このとき、次の問いに答えよ。
とする。このとき、次の問いに答えよ。
(1) bがaに限りなく近づくとき、Rはある点Aに限りなく近づく。Aの座標をaで表せ。
(2) 点Pが曲線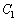 上を動くとき、(1)で求めた点Aが描く軌跡を
上を動くとき、(1)で求めた点Aが描く軌跡を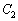 とする。曲線
とする。曲線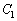 と軌跡
と軌跡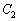 の概形を描き、
の概形を描き、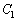 と
と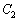 の交点の座標を求めよ。
の交点の座標を求めよ。 (3) 曲線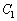 と軌跡
と軌跡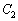 で囲まれた部分の面積を求めよ。
で囲まれた部分の面積を求めよ。 [解答へ]
電通大数学'08年後期[2]
関数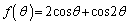 ,
,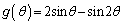 を用いて
を用いて
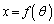 ,
, 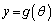
(1) 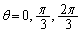 に対応するC上の点の座標を求めよ。
に対応するC上の点の座標を求めよ。 (2) 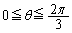 の範囲で
の範囲で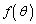 と
と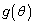 の増減を調べ、曲線Cの
の増減を調べ、曲線Cの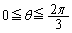 に対応する部分の概形を描け。
に対応する部分の概形を描け。 (3) C上の点をx軸に関して対称移動するとC上の点に移ることを示せ。
(4) C上の点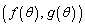 を原点を中心として
を原点を中心として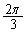 だけ回転すると、C上の点
だけ回転すると、C上の点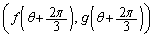 に移ることを示せ。
に移ることを示せ。 (5) 曲線Cの概形を描き、Cで囲まれる部分の面積Sを求めよ。
[解答へ]
茨城大理数学'09年[2]
関数
を考える。以下の各問いに答えよ。
(1) 関数fのグラフについて、座標軸との交点、凹凸、漸近線を調べ、その概形をかけ。
(2) x軸、y軸および関数fのグラフで囲まれた図形Aをx軸のまわりに1回転させて得られる立体の体積Vを求めよ。
(3) 部分積分法により
を求めよ。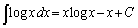 (Cは積分定数)を用いてよい。
(Cは積分定数)を用いてよい。 (4) (2)の図形Aをy軸のまわりに1回転して得られる立体の体積Wを求めよ。
[解答へ]
埼玉大工数学'09年[5]
次の問いに答えよ。
(1) 定積分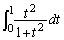 を求めよ。
を求めよ。 (2) 不等式
の定める立体の体積を求めよ。
[解答へ]
横浜国大工数学'08年前期[4]
連立不等式
の表す図形をx軸のまわりに回転してできる回転体の体積を求めよ。
[解答へ]
東京理科大理(数理)数学'09年[4]
対数を自然対数とする。数列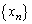 (
(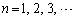 )を
)を
により定める。ただし、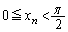 とする。次の問いに答えよ。
とする。次の問いに答えよ。
(1) 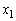 を求めよ。
を求めよ。 (2) 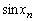 を求めよ。
を求めよ。 (3) 曲線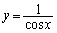 とx軸および2直線
とx軸および2直線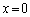 ,
,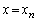 で囲まれた図形をx軸のまわりに1回転してできる回転体の体積を
で囲まれた図形をx軸のまわりに1回転してできる回転体の体積を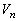 とする。
とする。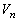 を求めよ。
を求めよ。 (4) (3)で求めた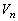 に対して、
に対して、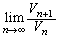 を求めよ。
を求めよ。 (5) (3)で求めた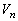 に対して、不等式
に対して、不等式 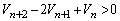 (
(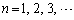 )
)が成り立つことを証明せよ。
[解答へ]
札幌医大数学'09年[3]
平面上に2点P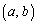 ,Q
,Q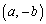 がある。ただしa,bは正の数とする。線分OPと線分OQ上に、それぞれ動点M,Nがあり、
がある。ただしa,bは正の数とする。線分OPと線分OQ上に、それぞれ動点M,Nがあり、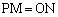 を満たすように動くとき、線分MNが通過する領域をTとする。ここでOは原点を表す。
を満たすように動くとき、線分MNが通過する領域をTとする。ここでOは原点を表す。
(1) 領域Tは線分OP,OQと、PとQを結ぶ曲線で囲まれる。この曲線の方程式を求めよ。
(2) 領域Tを図示せよ。
(3) 領域Tをx軸のまわりに1回転してできる立体をUとする。2点P,Qが単位円周上にあるとき、立体Uの体積を最大にするようなaの値と、そのときの立体Uの体積を求めよ。
[解答へ]
山梨大医数学'09年[4]
放物線A: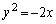 上の点
上の点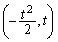 (
(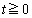 )における接線に関して、Aの頂点と対称な点Pのx座標、y座標を
)における接線に関して、Aの頂点と対称な点Pのx座標、y座標を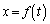 ,
,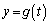 と表し、
と表し、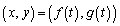 が描く曲線をBとする。
が描く曲線をBとする。
(2) 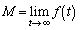 とする。
とする。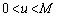 を満たす実数uに対して、曲線Bとx軸、直線
を満たす実数uに対して、曲線Bとx軸、直線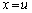 によって囲まれる図形の面積を
によって囲まれる図形の面積を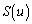 とするとき、
とするとき、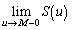 を求めよ。
を求めよ。 (3) 直線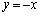 に関して放物線Aと対称な放物線をCとする。放物線Cをy軸方向に2倍拡大した放物線をDとする。放物線Dと放物線Aによって囲まれる図形の面積を求めよ。
に関して放物線Aと対称な放物線をCとする。放物線Cをy軸方向に2倍拡大した放物線をDとする。放物線Dと放物線Aによって囲まれる図形の面積を求めよ。 (4) 直線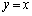 と放物線Dによって囲まれる図形を直線
と放物線Dによって囲まれる図形を直線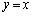 の周りに1回転してできる立体の体積を求めよ。
の周りに1回転してできる立体の体積を求めよ。 [解答へ]
早大理工数学'03年[5]
放物線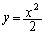 のうち、
のうち、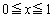 の部分をCとする。C上の点P
の部分をCとする。C上の点P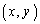 に対し、原点OからPまでのCの部分の長さをsで表す。xとyをsの関数とみなして
に対し、原点OからPまでのCの部分の長さをsで表す。xとyをsの関数とみなして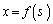 ,
,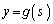 とおくとき、以下の問いに答えよ。
とおくとき、以下の問いに答えよ。
(1) 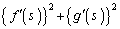 の値を求めよ。
の値を求めよ。 (2) 次の等式を示せ。
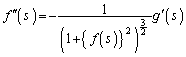 ,
,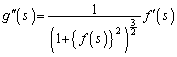
(3) PにおけるCの法線上にあり、Pとの距離が正の定数aである2点のうち、Cの下側にあるものをQ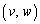 とする。v,wを
とする。v,wを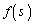 ,
,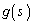 ,
,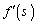 ,
,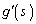 を用いて表せ。
を用いて表せ。 (4) Cの長さをLとし、PがC全体を動くときの、Qの描く曲線の長さをMとする。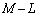 を求めよ。ただし、
を求めよ。ただし、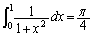 を用いてもよい。
を用いてもよい。 [解答へ]
名大数学'10年[2]
関数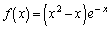 について、次の問いに答えよ。必要ならば、任意の自然数nに対して
について、次の問いに答えよ。必要ならば、任意の自然数nに対して
が成り立つことを用いてよい。
(1) 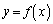 のグラフの変曲点を求め、グラフの概形をかけ。
のグラフの変曲点を求め、グラフの概形をかけ。 (2) 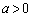 とする。点
とする。点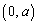 を通る
を通る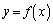 のグラフの接線が1本だけ存在するようなaの値を求めよ。また、aがその値をとるとき、
のグラフの接線が1本だけ存在するようなaの値を求めよ。また、aがその値をとるとき、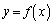 のグラフの
のグラフの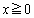 の部分、その接線およびy軸で囲まれた図形の面積を求めよ。
の部分、その接線およびy軸で囲まれた図形の面積を求めよ。 [解答へ]
阪大理系数学'10年後期[3]
曲線C: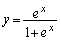 上に点A
上に点A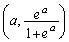 をとる。ただし、
をとる。ただし、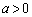 とする。
とする。
(1) C上にありAとは異なる点P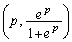 について、そこでの接線がAでの接線と平行となるようにpの値を定めよ。
について、そこでの接線がAでの接線と平行となるようにpの値を定めよ。 (2) pは上で定めた値とする。Cとx軸および2直線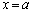 ,
,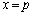 で囲まれた図形を、x軸のまわりに1回転させてできる回転体の体積を求めよ。
で囲まれた図形を、x軸のまわりに1回転させてできる回転体の体積を求めよ。 [解答へ]
九大理系数学'10年後期[1]
直線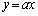 (ただしaは正の実数)をlとし、曲線
(ただしaは正の実数)をlとし、曲線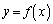 (ただし
(ただし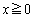 )をCとする。曲線Cが直線lの下側にあり、曲線C上の点
)をCとする。曲線Cが直線lの下側にあり、曲線C上の点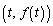 と直線lとの距離が
と直線lとの距離が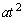 で表されるとき、以下の問いに答えよ。
で表されるとき、以下の問いに答えよ。
1.関数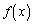 を求めよ。
を求めよ。 2.曲線Cとx軸で囲まれた図形を、x軸のまわりに回転させてできる回転体の体積Vを求めよ。
3.Vが最大となるようにaの値を定めよ。
[解答へ]
阪大理系数学'10年前期[4]
半径3の球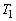 と半径1の球
と半径1の球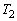 が、内接した状態で空間に固定されている。半径1の球Sが次の条件(A),(B)を同時にみたしながら動く。
が、内接した状態で空間に固定されている。半径1の球Sが次の条件(A),(B)を同時にみたしながら動く。
(A) Sは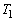 の内部にあるか
の内部にあるか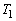 に内接している。
に内接している。 (B) Sは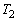 の外部にあるか
の外部にあるか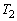 に外接している。
に外接している。 Sの中心が存在しうる範囲をDとするとき、立体Dの体積を求めよ。
[解答へ]
筑波大数学'10年[2]
3つの曲線
について以下の問に答えよ。
(1) 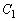 と
と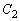 の交点、
の交点、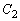 と
と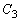 の交点、
の交点、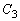 と
と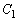 の交点のそれぞれについてy座標を求めよ。
の交点のそれぞれについてy座標を求めよ。 [解答へ]
京都府立医大数学'10年[3]
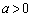 とし、座標平面上の2つの曲線
とし、座標平面上の2つの曲線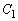 :
: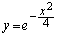 ,
,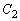 :
: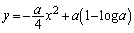 を考える。
を考える。
(1) 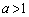 であるとき、
であるとき、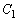 と
と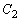 は共有点をもたないことを示せ。
は共有点をもたないことを示せ。 (2) 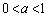 であるとき、
であるとき、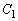 と
と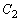 の共有点の座標をaを用いて表せ。
の共有点の座標をaを用いて表せ。 (3) (2)の場合で、共有点が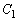 の変曲点であるとき、aの値を求めよ。
の変曲点であるとき、aの値を求めよ。 (4) aが(3)の値のとき、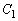 と
と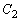 で囲まれた部分をy軸のまわりに1回転させてできる立体の体積を求めよ。
で囲まれた部分をy軸のまわりに1回転させてできる立体の体積を求めよ。 [解答へ]
北大理系数学'10年後期[2]
cを実数として、以下の問いに答えよ。
(1) すべての実数xに対して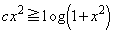 となるようなcの範囲を求めよ。
となるようなcの範囲を求めよ。 (2) cは(1)で求めた範囲にあるものとする。2つの曲線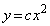 と
と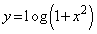 ,および、2つの直線
,および、2つの直線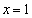 と
と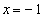 で囲まれる図形の面積が4となるcの値を求めよ。
で囲まれる図形の面積が4となるcの値を求めよ。 [解答へ]
東工大数学'11年後期[2]
次の式
で表されるxy平面上の曲線Cを考える。定数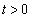 に対し、点P
に対し、点P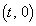 を通り、x軸に垂直な直線
を通り、x軸に垂直な直線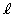 と曲線Cの交点をQとする。曲線C,x軸,y軸および直線
と曲線Cの交点をQとする。曲線C,x軸,y軸および直線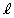 で囲まれた図形の面積を
で囲まれた図形の面積を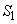 とし、△OPQの面積を
とし、△OPQの面積を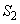 とする。
とする。
(1) 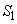 ,
,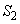 をtを用いて表せ。
をtを用いて表せ。 (2) 極限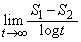 を求めよ。
を求めよ。 [解答へ]
横浜国大理工数学'11年前期[4]
xy平面上の2曲線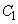 :
: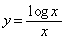 と
と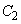 :
: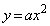 は点Pを共有し、Pにおいて共通の接線をもっている。ただし、aは定数とする。次の問いに答えよ。
は点Pを共有し、Pにおいて共通の接線をもっている。ただし、aは定数とする。次の問いに答えよ。
(1) 関数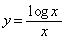 の増減、極値、グラフの凹凸、変曲点を調べ、
の増減、極値、グラフの凹凸、変曲点を調べ、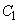 の概形を描け。ただし、
の概形を描け。ただし、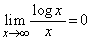 は証明なしに用いてよい。
は証明なしに用いてよい。 (2) Pの座標及びaの値を求めよ。
(3) 不定積分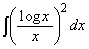 を求めよ。
を求めよ。 (4) 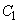 ,
,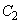 およびx軸で囲まれる部分を、x軸のまわりに1回転してできる立体の体積Vを求めよ。
およびx軸で囲まれる部分を、x軸のまわりに1回転してできる立体の体積Vを求めよ。 [解答へ]
名古屋市大芸工数学'11年[4]
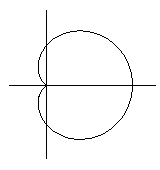 xy平面上において、媒介変数t (
xy平面上において、媒介変数t (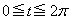 )によって
)によって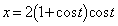 ,
,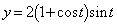 と表される右図の曲線について次の問いに答えよ。
と表される右図の曲線について次の問いに答えよ。
(1) xの最大値、最小値を求めよ。
(2) 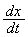 を求めよ。
を求めよ。 (3) この曲線で囲まれる図形をx軸のまわりに1回転してできる立体の体積を求めよ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
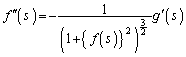 ,
,