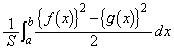極限演習問題
上智大理工数学'09年[1]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
極限値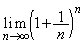 は自然対数の底eであり、その近似値は
は自然対数の底eであり、その近似値は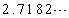 であることが知られている。ここでは、
であることが知られている。ここでは、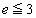 であることを次の手順で示そう。
であることを次の手順で示そう。
(1) 自然数kに対して、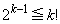 であることを示せ。
であることを示せ。 (2) 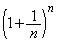 を二項定理を用いて展開することにより、
を二項定理を用いて展開することにより、 であることを示せ。
[解答へ]
神戸大理系数学'08年後期[5]
nを自然数とする。つぼの中に、1の数字を書いた玉が1個、2の数字を書いた玉が1個、3の数字を書いた玉が1個、・・・、nの数字を書いた玉が1個、合計n個の玉が入っている。つぼから無作為に玉を1個取り出し、書かれた数字を見て、元に戻す試行をn回おこなう。このとき、次の問いに答えよ。
(1) 試行をn回行ったとき、kの数字が書かれた玉をちょうどk回取り出す確率を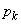 とする。
とする。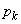 をkの式で表せ。ただし、
をkの式で表せ。ただし、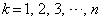 とする。
とする。 とおく。この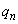 について、極限
について、極限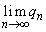 の値を求めよ。
の値を求めよ。 [解答へ]
神戸大理系数学'09年後期[3]
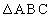 を考える。
を考える。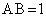 ,
,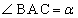 ,
,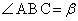 とし、α,β はいずれも、0と
とし、α,β はいずれも、0と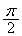 の間の角度とする。α,β,
の間の角度とする。α,β,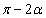 ,
,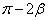 のいずれよりも小さい正の角度θ に対して、4点D,E,F,Gを次のように定める。
のいずれよりも小さい正の角度θ に対して、4点D,E,F,Gを次のように定める。
Dは、線分BC上にあって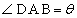 をみたす点Eは、線分AB上にあって
をみたす点Eは、線分AB上にあって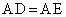 をみたす点Fは、線分AC上にあって
をみたす点Fは、線分AC上にあって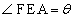 をみたす点Gは、線分AE上にあって
をみたす点Gは、線分AE上にあって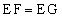 をみたす点
をみたす点 このとき、以下の問いに答えよ。
(1) 線分EGの長さをα,β,θ を用いて表せ。
(2) 極限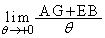 を求めよ。
を求めよ。 [解答へ]
鳥取大医数学'08年[4]
座標平面上に、直線l: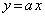 (
(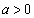 )と放物線C:
)と放物線C: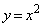 がある。lとCとで囲まれた領域をDとする。ただし、Dは境界を含む。領域Dに含まれ、かつ、x,yともに整数である点
がある。lとCとで囲まれた領域をDとする。ただし、Dは境界を含む。領域Dに含まれ、かつ、x,yともに整数である点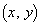 の個数を
の個数を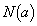 で表すとき、次の問いに答えよ。
で表すとき、次の問いに答えよ。
(1) 領域Dの面積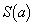 をaの式で表せ。
をaの式で表せ。 (3) kが正の整数のとき、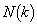 をkの式で表せ。
をkの式で表せ。 (4) 1以上の実数aに対して、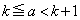 を満たす整数kをとるとき、
を満たす整数kをとるとき、 が成り立つことを示せ。
(5) 前問(1)で求めた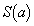 に対して、
に対して、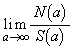 を求めよ。
を求めよ。 [解答へ]
熊本大理数学'07年後期[3]
数列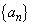 は
は
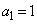 ,
,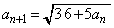 (
(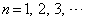 )
)
で与えられているとする。また、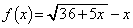 とし、xに関する方程式
とし、xに関する方程式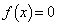 の正の解をaとする。このとき、次の問いに答えよ。
の正の解をaとする。このとき、次の問いに答えよ。
(1) aの値を求めよ。
(2) すべての正の整数nについて、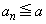 であることを証明せよ。
であることを証明せよ。 (3) 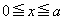 において、
において、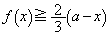 であることを証明せよ。
であることを証明せよ。 (4) 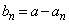 とするとき、すべての正の整数nについて、
とするとき、すべての正の整数nについて、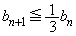 であることを証明せよ。
であることを証明せよ。 (5) 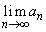 の値を求めよ。
の値を求めよ。 [解答へ]
長岡技科大数学'09年[2]
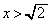 とする。
とする。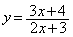 とするとき、以下の問いに答えよ。
とするとき、以下の問いに答えよ。
(1) 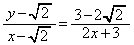 を示せ。
を示せ。 (2) 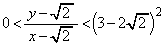 を示せ。
を示せ。 (3) 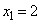 ,
,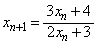 (
(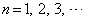 )で定義される数列を
)で定義される数列を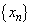 とする。
とする。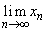 を求めよ。
を求めよ。 [解答へ]
岐阜大工数学'08年[4]
自然数nと実数xに対して
とおく。以下の問いに答えよ。
(1) 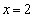 のとき、極限値
のとき、極限値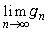 を求めよ。
を求めよ。 (2) すべての実数xに対して、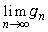 が存在することを示せ。また、
が存在することを示せ。また、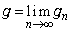 とおくとき、gをxを用いて表せ。
とおくとき、gをxを用いて表せ。 (3) xの値がすべての実数を変化するとき、(2)で定まったgの最大値と最小値を求めよ。
[解答へ]
長崎大工数学'08年[3]
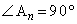 ,
,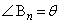 である相似な直角三角形
である相似な直角三角形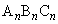 (
(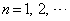 )が、次のような規則で座標平面上に並べられている。
)が、次のような規則で座標平面上に並べられている。
規則1) 三角形どうしが、辺以外で重なることはない。
規則2) 頂点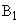 は座標平面上の原点
は座標平面上の原点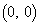 と一致し、
と一致し、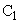 は点
は点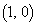 と一致している。また、
と一致している。また、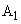 は第1象限にある。
は第1象限にある。 規則3) mを自然数とするとき、三角形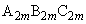 と三角形
と三角形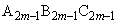 において、
において、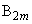 は
は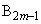 と一致し、
と一致し、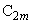 は
は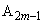 と一致している。
と一致している。 さらに、三角形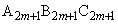 と三角形
と三角形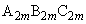 において、頂点
において、頂点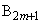 は
は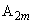 と一致し、
と一致し、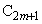 は
は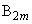 と一致している。
と一致している。 次の問いに答えよ。
(1) 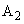 の座標を、θ を用いて表せ。
の座標を、θ を用いて表せ。 (3) 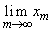 および
および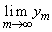 を求めよ。
を求めよ。 [解答へ]
北大数学'10年後期[3]
1辺の長さがaの正三角形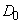 から出発して、多角形
から出発して、多角形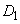 ,
,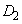 ,・・・,
,・・・,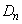 ,・・・・・・ を次のように定める。
,・・・・・・ を次のように定める。
(i) ABを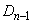 の1辺とする。辺ABを3等分し、その分点をAに近い方からP,Qとする。
の1辺とする。辺ABを3等分し、その分点をAに近い方からP,Qとする。 (ii) PQを1辺とする正三角形PQRを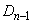 の外側に作る。
の外側に作る。 (iii) 辺ABを折れ線APRQBで置き換える。
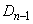 のすべての辺に対して(i)〜(iii)の操作を行って得られる多角形を
のすべての辺に対して(i)〜(iii)の操作を行って得られる多角形を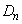 とする。
とする。
以下の問いに答えよ。
(1) 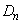 の周の長さ
の周の長さ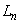 をaとnで表せ。
をaとnで表せ。 (2) 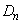 の面積
の面積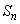 をaとnで表せ。
をaとnで表せ。 (3) 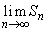 を求めよ。
を求めよ。 [解答へ]
北大理系数学'08年前期[3]
関数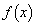 を
を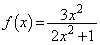 とする。
とする。
(1) 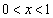 ならば、
ならば、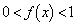 となることを示せ。
となることを示せ。 (2) 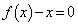 となるxをすべて求めよ。
となるxをすべて求めよ。 (3) 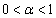 とし、数列
とし、数列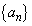 を
を とする。αの値に応じて、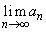 を求めよ。
を求めよ。 [解答へ]
大分大医数学'09年[1]
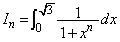 (
(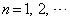 )
)
とおくとき、次の問いに答えよ。
(1) 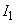 ,
,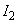 の値を求めよ。
の値を求めよ。 (2) 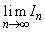 の値を求めよ。
の値を求めよ。 [解答へ]
大阪府立大工数学'09年[5]
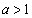 ,
,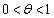 とする。このとき、次の問いに答えよ。
とする。このとき、次の問いに答えよ。
(1) 積分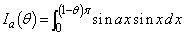 を計算し、
を計算し、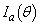 をaとθ を用いて表せ。
をaとθ を用いて表せ。 (2) 極限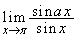 が正の値に収束するためのaの条件を求めよ。
が正の値に収束するためのaの条件を求めよ。 (3) (2)の条件を満たすaに対して、極限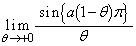 をaを用いて表せ。
をaを用いて表せ。 (4) (2)の条件を満たすaに対して、極限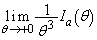 をaを用いて表せ。なお、
をaを用いて表せ。なお、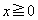 であるすべてのxに対して
であるすべてのxに対して が成り立つことを用いてもよい。
[解答へ]
東工大数学'95年前期[3]
nを自然数とする。
(1) 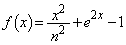 の増減を調べ、グラフの概形を描け。
の増減を調べ、グラフの概形を描け。 (2) 楕円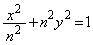 と曲線
と曲線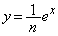 の交点のうち
の交点のうち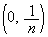 でない方の座標を
でない方の座標を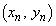 とおく。このとき、
とおく。このとき、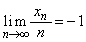 であることを示せ。
であることを示せ。 [解答へ]
名工大数学'09年前期[3]
実数xに対して
とおく。
(1) 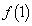 を求めよ。
を求めよ。 (2) 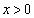 に対して
に対して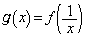 とおく。
とおく。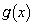 の導関数を求め、
の導関数を求め、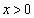 に対して等式
に対して等式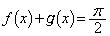 が成り立つことを示せ。
が成り立つことを示せ。 (3) (2)を利用して極限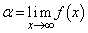 を求めよ。
を求めよ。 (4) 極限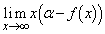 を求めよ。
を求めよ。 [解答へ]
防衛医大数学'09年[1]
曲線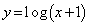 上の点P
上の点P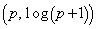 における接線と法線をそれぞれ
における接線と法線をそれぞれ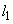 ,
,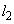 とする。曲線と接線
とする。曲線と接線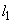 とy軸で囲まれる部分の面積を
とy軸で囲まれる部分の面積を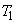 ,曲線と法線
,曲線と法線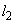 とy軸で囲まれる部分の面積を
とy軸で囲まれる部分の面積を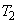 とする。ただし、
とする。ただし、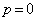 のとき、
のとき、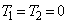 とおく。
とおく。
このとき、以下の問いに答えよ。
(1) 接線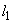 と法線
と法線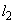 の方程式を求めよ。
の方程式を求めよ。 (2) 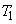 ,
,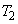 をpを用いて表せ。
をpを用いて表せ。 (3) 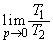 を求めよ。
を求めよ。 [解答へ]
奈良県立医大数学'09年[4]
(1) 任意の正整数nに対して関数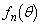 は
は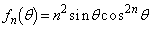 で定義されているものとする。このとき、
で定義されているものとする。このとき、 が成り立つかどうか調べよ。
(2) 各正整数nに対して、θ が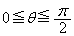 の範囲を動くときの関数
の範囲を動くときの関数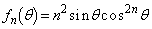 の最大値を
の最大値を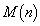 とおく。このとき、極限値
とおく。このとき、極限値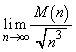 を求めよ。
を求めよ。 ただし、aを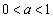 の範囲にある定数とするとき、
の範囲にある定数とするとき、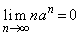 であることは証明なしに用いてよい。
であることは証明なしに用いてよい。 [解答へ]
熊本大医数学'10年[4]
以下の問いに答えよ。
(問1) pを0でない定数とする。関数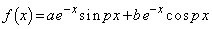 について、
について、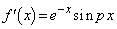 となるように、定数a,bを定めよ。
となるように、定数a,bを定めよ。 (問3) 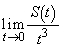 の値を求めよ。
の値を求めよ。 [解答へ]
大阪市大数学'10年[4]
a,bは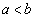 をみたす実数とする。
をみたす実数とする。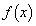 ,
,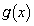 は閉区間
は閉区間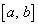 で定義された連続関数で、
で定義された連続関数で、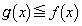 をみたすとする。座標平面上、不等式
をみたすとする。座標平面上、不等式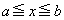 ,
,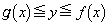 をみたす点
をみたす点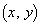 全体からなる図形をAとする。Aの面積Sが正のとき、Aの重心のy座標は、
全体からなる図形をAとする。Aの面積Sが正のとき、Aの重心のy座標は、
で与えられる。この事実を用いて、次の問いに答えよ。
問1 rは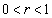 をみたす実数とする。不等式
をみたす実数とする。不等式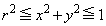 ,
,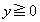 をみたす点
をみたす点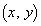 全体からなる図形をBとおく。Bの重心のy座標
全体からなる図形をBとおく。Bの重心のy座標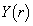 をrを用いて表せ。
をrを用いて表せ。 問2 tは正の実数とする。不等式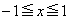 ,
,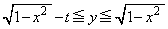 をみたす点
をみたす点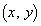 全体からなる図形をCとおく。Cの重心のy座標
全体からなる図形をCとおく。Cの重心のy座標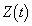 をtを用いて表せ。
をtを用いて表せ。 問3 問1で得られた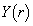 と問2で得られた
と問2で得られた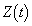 について、
について、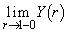 ,
,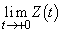 の大小を比較せよ。
の大小を比較せよ。 [解答へ]
東北大理系数学'10年後期[4]
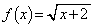 として、数列
として、数列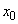 ,
,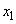 ,
,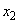 ,・・・ を
,・・・ を
で定義する。以下の問いに答えよ。
(1) すべての自然数nに対して
が成り立つことを示せ。
(2) すべての自然数nに対して
が成り立つことを示せ。
(3) すべての自然数nに対して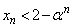 を満たす正の定数αのうち、最大のものを求めよ。
を満たす正の定数αのうち、最大のものを求めよ。 [解答へ]
広島大理系数学'10年後期[1]
自然数のうち、2と8がどの桁にも現れないものを考え、それらを小さい方から重に並べた数列
1, 3, 4, 5, 6, 7, 9, 10, 11, 13, 14, 15, 16, 17, 19, 30, 31, 33, ・・・
を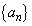 とする。いま、自然数mに対し、数列
とする。いま、自然数mに対し、数列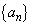 の中にあるm桁の整数の個数を
の中にあるm桁の整数の個数を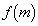 とする。例えば
とする。例えば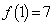 である。このとき、以下の問いに答えよ。
である。このとき、以下の問いに答えよ。
(1) 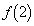 ,
,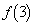 を求めよ。
を求めよ。 (2) 自然数mに対し、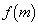 を求めよ。
を求めよ。 (3) 自然数mに対し、数列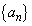 の中にあるm桁の整数の逆数の総和は
の中にあるm桁の整数の逆数の総和は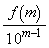 より小さいことを示せ。
より小さいことを示せ。 (4) すべての自然数nに対し、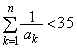 が成り立つことを示せ。
が成り立つことを示せ。 [解答へ]
東工大数学'10年後期[1]
a,b,tは実数で、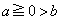 とする。次の漸化式により、数列
とする。次の漸化式により、数列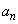 ,
,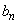 (
(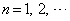 )を定める。
)を定める。
(1) 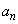 をa,b,t,nを用いて表せ。
をa,b,t,nを用いて表せ。 (2) 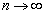 とするとき、
とするとき、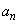 が収束するためのa,b,tについての必要十分条件を求めよ。
が収束するためのa,b,tについての必要十分条件を求めよ。 [解答へ]
山梨大医数学'10年[2]
表が出る確率がp,裏が出る確率が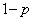 である硬貨をn回投げる。このとき、硬貨を1回投げるごとに、表ならばAを記録し、裏ならばBを記録して、1回目から順番に1列に並べる。ただし、nは2以上の整数であり、
である硬貨をn回投げる。このとき、硬貨を1回投げるごとに、表ならばAを記録し、裏ならばBを記録して、1回目から順番に1列に並べる。ただし、nは2以上の整数であり、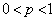 とする。このように並べたn個の文字の中に
とする。このように並べたn個の文字の中に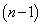 組ある連続する2文字が、どれもABの順番に並んでいない確率を
組ある連続する2文字が、どれもABの順番に並んでいない確率を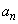 とし、どれもAAの順番に並んでいない確率を
とし、どれもAAの順番に並んでいない確率を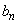 とする。
とする。
(1) 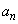 を求めよ。
を求めよ。 (2) 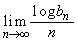 を求めよ。
を求めよ。 (3) 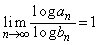 となるようなpの値、および、そのときの
となるようなpの値、および、そのときの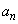 ,
,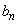 を求めよ。ただし、
を求めよ。ただし、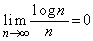 となることを用いてもよい。
となることを用いてもよい。 [解答へ]
同志社大理工数学'11年[4]
数列
は漸化式
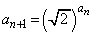 (
(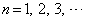 )
)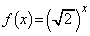 として次の問に答えよ。
として次の問に答えよ。
(1) 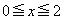 における
における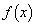 の最大値と最小値を求めよ。
の最大値と最小値を求めよ。 (2) 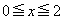 における
における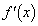 の最大値と最小値を求めよ。
の最大値と最小値を求めよ。 (3) 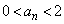 (
(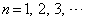 )が成立することを数学的帰納法を用いて示せ。
)が成立することを数学的帰納法を用いて示せ。 (4) 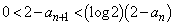 (
(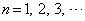 )が成立することを示せ。
)が成立することを示せ。 (5) 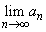 を求めよ。
を求めよ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 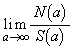 を求めよ。
を求めよ。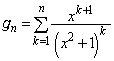
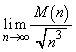 を求めよ。
を求めよ。