積分法
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学Ⅲの積分では、三角関数、指数関数、対数関数を含む関数の積分も扱います。これらの積分には、置換積分法、部分積分法などの技巧が必要になります。また、区分求積法により、積分の原理を学びます。
積分法を応用することにより、面積、体積、曲線の長さなどの計算を行うことができます。ここでは、種々の曲線について、面積、体積の計算を行った例も取り上げます。
この項目では、不定積分、定積分、定積分の公式、定積分と微分、定積分と面積、絶対値を含む積分の項目も参照してください。
ここで学習する内容は、以下の通りです。各項目をクリックしてください。
不定積分の公式 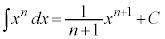 (
(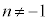 ),
),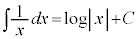 ,
,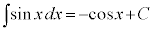 ,
,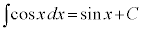 ,
,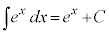 ,
,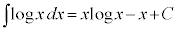
置換積分 そのままの形では積分計算ができなくても、被積分関数の中の式を文字に置き換えたり、文字を式に置き換えたりすると、積分計算が行える場合があります。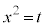 ,
,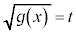 ,
,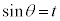 ,
,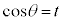 ,
,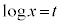 ,
,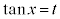 の置き換えを扱います。
の置き換えを扱います。
置換積分(その2) 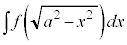 では、
では、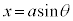 とおき、
とおき、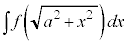 では、
では、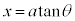 とおくとうまくいくことがあります。
とおくとうまくいくことがあります。
部分積分法 公式: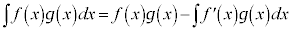 により積分が行える場合があります。
により積分が行える場合があります。
定積分の漸化式 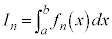 というタイプの漸化式を考えます。
というタイプの漸化式を考えます。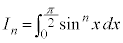 の漸化式:
の漸化式: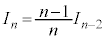
偶関数・奇関数の積分 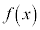 が偶関数であるとき、
が偶関数であるとき、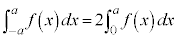 ,
,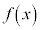 が奇関数であるとき、
が奇関数であるとき、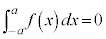
三角関数の積分 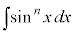 という形の積分は、nに入る自然数によって計算のしかたを工夫する必要があります。
という形の積分は、nに入る自然数によって計算のしかたを工夫する必要があります。
分数関数の積分 分母、分子がxの整式であるような分数関数は、部分分数に分けることによって積分を実行します。
置換積分(その3) 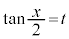 ,
,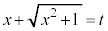 の置き換えを扱います。
の置き換えを扱います。
定積分と微分(その2) 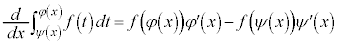
区分求積法 定積分が面積を表していることを確認します。無限級数を定積分に変換する公式: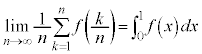
定積分と不等式 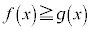 のとき、
のとき、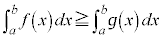
階段関数と不等式 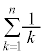 のような数列和は求められないので、定積分を利用して不等式で評価します。
のような数列和は求められないので、定積分を利用して不等式で評価します。
コーシー・シュワルツの不等式 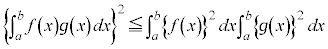
定積分と面積(その2) 数学Ⅱでは扱わなかった関数のグラフについて面積を考えます。
定積分と体積 断面積を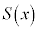 として、
として、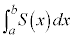 によって立体の体積を計算することができます。
によって立体の体積を計算することができます。
x軸のまわりの回転体 x軸のまわりの回転体の体積は、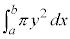 として計算できます。
として計算できます。
y軸のまわりの回転体 y軸のまわりの回転体の体積は、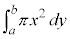 として計算できます。円筒分割にも触れます。
として計算できます。円筒分割にも触れます。
斜回転体 曲線を直線: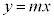 のまわりに1回転させたときにできる回転体の体積を求める方法を考えます。
のまわりに1回転させたときにできる回転体の体積を求める方法を考えます。
曲線の長さ 曲線: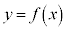 の長さは、
の長さは、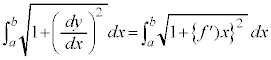 として計算できます。
として計算できます。
サイクロイド 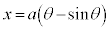 ,
,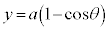 で与えられる曲線をサイクロイドと言います。
で与えられる曲線をサイクロイドと言います。
アステロイド 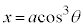 ,
,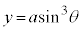 で与えられる曲線をアステロイドと言います。
で与えられる曲線をアステロイドと言います。
カージオイド 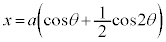 ,
,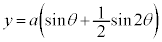 (
(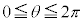 ) で与えられる曲線をカージオイドと言います。
) で与えられる曲線をカージオイドと言います。
エピサイクロイド 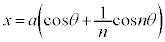 ,
,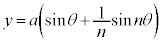 で表される曲線をエピサイクロイドと言います。
で表される曲線をエピサイクロイドと言います。
ハイポサイクロイド 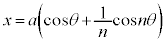 ,
,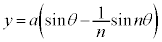 で表される曲線をハイポサイクロイドと言います。
で表される曲線をハイポサイクロイドと言います。
物理への応用 微積分を使って物理の問題を考えます。ここでは、速度、加速度、等加速度運動、等速円運動を扱います。
物理への応用(その2) 「物理への応用」の続きです。ここでは、単振動、また、速度に比例する抵抗力が働く運動を扱います。
減衰振動関数 「物理への応用(その2)」で出てくる減衰振動関数は、大学入試でも頻出です。グラフ、面積を考えます。
フーリエ級数 関数を正弦・余弦の級数和として表すという技巧があります。それに必要となる定積分の計算法を学びます。
積分方程式 積分を含む等式を積分方程式を言います。ここでは、大学入試に出題されるレベルのものを扱います。
微分方程式 導関数や元の関数を含む等式を微分方程式と言います。変数分離型などの簡単なものを扱います。
微分方程式(その2) 微分方程式のうちでやや技巧の必要な、線形1階、線形2階の微分方程式を扱います。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 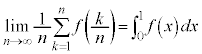
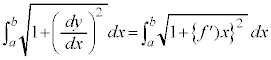 として計算できます。
として計算できます。